К вопросу о реализации профессиональной направленности обучения математическим дисциплинам в техническом вузе

Образование сегодня — одна из самых важных сфер человеческой деятельности, огромные достежения в этой области лезли в основу грандиозных социальных и научно-технологических преобразований, стали основой глобальной системы открытого, гибкого, индивидуализированного созидающего знания. В этих условиях изменилась роль учебных заведений в совершенствований самого образования с целью достижения наиболее оптимальных результатов. Для вузов — это новые знания, совершенные уумения и навыки, наибольшая информированность студентов.

Для технических вузов, в первую очередь, это высококвалифицированный педагогический персонал, который способен мотивировать студентов, вызвать у них желание заниматься с интересом, а, что особенно важно для математических дисциплин — показать их связь с будущей професией. Посмотрим, как это важно сделать на примере дифференциальных уравнений. Умелое владение теоретическим материалом позволит педагогу в ходе лекции объяснить студентам, что с их помощью описываются проще и полнее прикладные процессы, в частности, связанные с физикой, теоретической механикой, сопротивлением материалов, гидравликой, теорией машин и механизмов.

Обыкновенные дифференциальные уравнения для студентов инженерных специальностей являются фундаментом для многих других разделов высшей математики: уравнений, с частными производными, уравнений математической физики, вариационного исчисления и служат одним из механизмов глубокого изучения механики, физики и других естественных дисциплин.

Изучать дифференциальные уравнения студенты начинают на базе полученных знаний по линейной алгебре и аналитической геометрии, дифференциальным и интегральным исчислениям функциям одной переменной, функциям нескольких переменных, кратным и криволинейным интегралам.

Такая подготовка помогает осуществлять профессиональную направленность обучения студентов дифференциальным уравнениям. Задача педагога не просто расширить представления студентов о значимости дифференциальных уравнений в специальных дисциплинах математического образования инженера — механика, но и научить его строить математические модели на базе дифференциальных уравнений, вызывая интерес студентов к активизации учебной деятельности, стремление к углублению математической подготовки, детальному изучению предложенного материала для получения оптимальных для выпускника вуза профессиональных навыков.

Эта задача, несомненно, выполнима при условий, что педагог согласует теорию дифференциальных уравнений с имеющимися у студентов базовыми знаниями обеспечивает формирование навыков эвристического, прогностического мышления на основе педагогических инноваций; сопровождает информационное изложение с проблемно-поисковыми методами, создавая ситуации поиска теоретических обобщений, прогнозирование перспектив их применения для описания процессов и устройств, которые им придется изучать в спецдисциплинах; стимулирует восприятие математики как дисциплины профессионально значимой. Последнее особенно важно, т. к. студенты зачастую представляют «Дифференциальные уравнения» как нечто абстрактное, не способное решать профессионально значимых задач, а потому не знают и не умеют применять их для описания изучаемых процессов и устройств.

Отсюда следует, что педагог должен стремиться к тому, чтобы учебный материал был насыщен задачами и примерами, показывающими, где и как можно применить дифференциальные уравнения, как использовать теоретический материал по этой теме.

Кроме того, лекция должна сопровождаться постоянным общением преподавателя со студентами, т. е. диалогом, который поможет реализовать главную задачу лекции — раскрыть сущность основных понятий, идей и теорий по изучаемому вопросу, ознакомить студентов со способами применения теории на практике, сформировать интерес к предмету.

Так, например, при изучении курса «Высшая математика» лекций по разделу «Дифференциальные уравнения» должны соответствовать учебному плану и обязательно включать:

-        задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными;

-        однородные дифференциальные уравнения первого порядка;

-        понятие о дифференциальных уравнениях высших порядков;

-        линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами;

-        структуру общего решения линейного неоднородного уравнения;

-        линейные дифференциальные уравнения с постоянными коэффициентами высших порядков.

Выбрав тему лекции: «Дифференциальные уравнения первого порядка», покажем возможности и профильной направленности. Прежде всего, надо сформировать положительное отношение к изучаемому материалу, дабы побудить студентов к желанию его изучать. Для этого привести соответствующие аргументы. С начала необходимо убедить студентов, что дифференциальные уравнения являются аппаратом, с помощью которого можно изучать процессы, протекающие в природе, в частности такие как: радиоактивный распад, увеличение колоний бактерий, поглощение света при прохождении через некоторую среду, движение тела в сопротивляющейся среде и многие другие, но что особенно следует выделить — это феномен, заключающий в том, что все эти процессы можно решить помощью одного и того же уравнения: у' = ку, которое показывает, что во всех этих вопросах мгновенная скорость изменения некоторой величины пропорциональна значению этой величины в данный момент времени.

Далее следует ознакомить студентов с такой установкой: использование дифференциальных уравнений позволяет предсказывать течение некоторых событий. Так, уравнения небесной механики дают возможность предсказать поведение небесных тел, уравнения квантовой механики — течение событий в микромире, т. е. математически сформулированная теория открывает невиданные возможности для предсказания новых, доселе неизвестных явлений (например, открытие планеты Нептун Леверье, предсказание Максвеллом электромагнитного поля, Дираком — позитрона и др.).

Изучение дифференциальных уравнений следует начинать с проблемы, предложенной в виде задачи, приводящей к дифференциальному уравнению. Ознакомив с условием задачи, педагог показывает этапы ее решения: сначала необходимо формализовать исходную задачу, перевести ее условия на адекватный математический язык, т. е. в нашем случае язык дифференциальных уравнений. Это значит, что следует ввести неизвестные параметры и функции и выразить через них известные параметры:

-        основные физические величины, затем составить уравнение (или уравнения), что и завершит этап формализации;

Следующий этап — решение модельной задачи, которая сводится к решению уравнения т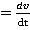 = -kv., где v-неизвестная функция от t; k, m — постоянные. Это уравнение и есть простейшее дифференциальное уравнение.

Для интегрального исчисления функции одной переменной с необходимо отыскивать неизвестную функцию по ее производной или дифференциалу. Значит, чтобы решить данное уравнение, нужно рассортировать переменные и получить возможность провести интегрирование.

Интегрирование уравнения после рассортирования переменных выглядит так:

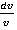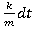=; lnv=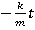+c; v=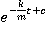==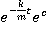c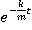

Третий этап — интерпретация полученного решения — сводится к соотношению полученных результатов с исходной ситуацией. Подставляя числовые данные исходя из условия задачи найдем ту функцию, которая удовлетворяет заданной ситуации.

На предложенном педагогом примере студенты должны убедиться, что чисто практическая задача описывается новым для них понятием — дифференциальное уравнение. Обосновав необходимость изучения этой темы, педагог переходит к изучению методов решения дифференциальных уравнений, в месте со студентами создает математический аппарат, т. е. раскрывает методы решения дифференциальных уравнений.

И здесь задача заключается в том, чтобы лекция не была сообщением готовых знаний, а давала толчок к самостоятельности и творчеству» [3,с. 107].

Проблемное построение лекций, станет тем ключом, который обеспечит процесс познания студентов приближенный к поисковой, исследовательской деятельности, что позволит не только усвоить теоретические знания но развить теоретическое мышление, сформировать познавательный интерес к содержанию учебного предмета и профессиональной мотивации будущего специалиста [1].

Основная задача лектора приобщить студентов к объективным противоречиям развития научного знания и способам их разрешения с целью активизации мыслительной деятельности, познавательной активности. И она решается, т. к. на проблемной лекции новое знание вводится как неизвестное для студентов, что создает иллюзию «открытия». Ведь студент не просто перерабатывает информацию, а усваивая ее как субъективное открытие неизвестного для себя знания.

Для закрепления полученных знаний необходима организация целенаправленная активная деятельность направленная на сознательное усвоение теоретических знаний. Диалогическое общение преподавателя со студентами решает эту задачу.

В качестве примера диалога преподавателя с аудиторией, приведем фрагмент лекции по теме «Линейные дифференциальные уравнения первого порядка», на котором решается следующая задача.

Задача. К источнику ЭДС подключается контур, состоящий из последовательно соединенных катушки индуктивности L и сопротивления R. Найти I(t) после замыкания цепи, если в начальный момент времени I(t) =0.

Решение задачи педагог сопровождает комментарием, о том, что при всех изменениях режима электрической цепи имеют место переходные процессы, которые протекают не мгновенно, а изменяются во времени, так как электромагнитном поле цепи остаются некоторая энергия, что сила тока I(t) на любом участке одинакова и предлагает студентам вспомнить известные законы теории электрических цепей для решения задачи.

Студенты вспоминают второй закон Кирхгофа, по которому алгебраическая сумма мгновенных значений ЭДС, действующих в замкнутом контуре, равна алгебраической сумме мгновенных значений напряжений его отдельных участков, т. е.

E = U_L+U_R,

где U_L = L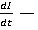падение напряжения на индуктивности;

U_R=RI — падение напряжений на сопротивлении.

В результате получаем уравнение L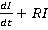= Е.

Затем в месте с ппреподавателем определяют вид полученного уравнения как линейного дифференциального уравнения первого порядка относительно функции I(t) и выбирают путь его решения с помощью подстановки формулы Эйлера-Бернулли. Затем педагог резюмирует полученный результат, привлекая к его формулировке и студентов.

Иногда целесообразно закончить лекцию поставив проблемный вопрос для того, чтобы решить его на практическом занятии, т. е. позволить студентам самим подумать над проблемой вне аудитории, используя конспект лекций, справочную литературу.

Так, например, можно при решении приведенной выше задачи предложить объяснить физический смысл полученного решения в случае размыкания электрической цепи (это можно сделать на следующей лекции или практическом занятии, подчеркнув важность применения последовательного чередования замыкания и размыкания цепи в практике, например, при телеграфировании).

После изучения темы «Неоднородные линейные уравнения 2-гопорядка» студентам можно предложить изучить колебания материальной точки массы m, находящейся под действием упругой силы, величина которой пропорциональна отклонению х точки от положения равновесия, при наличии периодической возмущающей силы, численно равной F = F₀ sinpt (в случае, когда частота внешней силы совпадает с частотой свободных колебаний) и на основе полученного уравнения объяснить явление, которое носит название резонанса.

Здесь внимание педагога должно быть направлено на обязательное систематическое ведение студентами конспекта лекции, что позволяет обратиться к объяснению педагога в случае, если студент затрудняется в определении типа, к которому относится дифференциальное уравнение, и, как следствие этого, неправильно решает его.

Полный конспект лекции позволит вспомнить изученный ранее материала и, ориентируясь на составленные в месте, с педагогом алгоритмические схемы классификации дифференциальных уравнений, выделить главное, усвоить его и решить предложенные задачи и примеры.

Итак, теоретический материал, презентуемый студентам технических вузов в форме лекций, должен быть доступен, интересен и мотивирован на использование его, в частности, в части, касающейся математики, для профильной направленности, связан с обоснованием прикладного ее значения, а именно дифференциальных уравнений, в инженерных профессиях.

Непреходящее значение для прочного усвоения материала имеет создание в аудитории творческой атмосфере, желание дискутировать, вовлечение студентов в конструктивный диалог с преподавателем. При этом особое внимание акцентируется на необходимость и широкую возможность использования математических моделей в решении практических инженерных задач. Методы, используемые педагогом, могут быть самого широкого спектра — от решения простых примеров и задач до создания алгоритмов и проблемно-поисковых, создания ситуации поиска и обобщений, прогнозирования перспектив.

Литература:

1.         Матюшкин A. M. Проблемы развития профессионального теоретического мышления. М., 1980. С.3–47.

2.         Shadiev R,D., Turdiyev Sh.R. On questions of particularities of teaching mathematics in technical higher education institutions (HEI). Austrian Journal of Humanities and Social Sciences № 9–10.Vienna, 2014.рр 141–144.

3.         Сластенин В. И. Научно-исследовательская работа студентов и формирование творческой личности учителя // Организация научно- исследовательской работы в пед. институтах: Материалы Всерос. совещ.-семинара.- Казань, 1973. — С. 102–112.

4.         Шадиев Р. Д. Методолого-дидактические основы анализа учебных текстов. Ташкент.: ФАН, 2004. -105с.