Одним из новых явлений для педагогики является понятие «технологии», часто встречающиеся в педагогической литературе (научной, публицистической, учебной). В педагогической и психологической литературе часто встречается понятие «технология», пришедшее к нам вместе с развитием компьютерной техники и внедрением новых компьютерных технологий. В педагогической науке появилось специальное направление — педагогическая технология. Это направление зародилось в 60-е годы в США, Англии и в настоящее время распространилось практически во всех странах мира. Появление этого термина и направления исследований в педагогике не являются случайностью.
Понятие «педагогическая технология» может рассматриваться в трех аспектах:
научном — как часть педагогической науки, изучающая и разрабатывающая цели, содержание и методы обучения и проектирующая педагогические процессы;
процессуальном — как описание (алгоритм) процесса, совокупность целей, содержания, методов и средств достижения планируемых результатов обучения;
деятельностном — осуществление технологического (педагогического) процесса, функционирование всех личностных, инструментальных и методологических педагогических средств.
В энциклопедическом словаре дается следующее определение: технология — это «совокупность методов обработки, изготовления, изменения состояния, свойств, формы сырья, материала или полуфабриката, осуществляемых в процессе производства продукции» [16, с.1338].
В толковом словаре живого великорусского языка В.Даля под технологией понимается «совокупность приемов, применяемых в каком — либо деле, мастерстве, искусстве» [3, c 404].
В толковом словаре С. И. Ожегова технология рассматривается как совокупность производственных процессов в определенной отрасли производства, а также научное описание способов производства: «Технология — это одновременно система совокупности знаний, умений, навыков, методов, способов деятельности и алгоритм, научная разработка решения каких — либо проблем» [8, с.708].
Содержание понятия «технология» раскрывается и уточняется в зависимости от области человеческой деятельности.
Технология обучения — это совокупность методов и средств обработки, представления, изменения и предъявления учебной информации, с другой — это наука о способах воздействия преподавателя на учеников в процессе обучения с использованием необходимых технических или информационных средств. В технологии обучения содержание, методы и средства обучения находятся во взаимосвязи и взаимообусловленности. Педагогическое мастерство учителя состоит в том, чтобы отобрать нужное содержание, применить оптимальные методы и средства обучения в соответствии с программой и поставленными образовательными задачами. Технология обучения — системная категория, структурными составляющими которой являются:
цели обучения;
содержание обучения;
средства педагогического взаимодействия;
организация учебного процесса;
ученик, учитель;
результат деятельности.
Таким образом, технология обучения:
повышает производительность труда учителя;
способствует тому, что контроль результативности обучения каждого учащегося и система обратной связи позволяют обучать учащихся в соответствии с их индивидуальными возможностями и складом характера;
освобождает время учителя посредством перекладывания основных функций обучения на средства обучения, в результате он больше внимания может уделить вопросам индивидуального и личностного развития учащихся;
так как для любой технологии цель определяется очень точно, то использование объективных методов контроля дает возможность снизить роль субъективного фактора при проведении контроля;
создание технологий обучения позволяет снизить зависимость результата обучения от уровня квалификации учителя, что открывает возможности для выравнивания уровней освоения учебной дисциплины учащимися во всех образовательных учреждениях;
технологизация создает предпосылки для решения проблемы преемственности образовательных программ школьного и профессионального образования.
В технологическом подходе к обучению выделяют следующие этапы:
постановка целей и их максимальное уточнение с ориентацией на достижение результатов;
подготовка учебных материалов и организация всего хода обучения в соответствии с учебными целями;
оценка текущих результатов;
коррекция обучения, направленная на достижение поставленных целей;
заключительная оценка результатов [5, с.4].
По категории обучающихся наиболее важными и оригинальными являются:
массовая (традиционная) школьная технология, рассчитанная на усредненного ученика;
технологии продвинутого уровня (углубленного изучения предметов, гимназического, лицейского, специального образования и др.);
технологии компенсирующего обучения (педагогической коррекции, поддержки, выравнивания и т. п.);
различные виктимологические технологии (сурдо-; орто-; тифло- и олигофренопедагогика);
технологии работы с отклоняющимися (трудными и одаренными) детьми в рамках массовой школы.
Как и любая технология, педагогическая технология представляет собой процесс, при котором происходит качественное изменение воздействия на обучаемого. Педагогическую технологию можно представить следующей формулой:
ПТ = цели + задачи + содержание + методы (приемы, средства) + формы обучения.
Организация и реализация этого процесса (педагогической технологии) зависит от требований ведущих дидактических принципов. Дидактические принципы,или принципы обучения — это руководящие положения, принципиальные закономерности, которые направляют деятельность преподавателя, помогают определить содержание обучения, методы и формы обучения. К основным дидактическим принципам относятся:
принцип научности и доступности обучения;
принцип системности обучения и связи теории с практикой;
принцип сознательности и активности учащихся в обучении при руководящей роли учителя;
принцип наглядности;
принцип прочности усвоения знаний и связи обучения с всесторонним развитием личности учащихся.
Одна и та же технология в руках разных исполнителей может каждый раз выглядеть по-иному: здесь неизбежно присутствие личностной компоненты мастера, особенностей контингента учащихся, их общего настроения и психологического климата в классе. Результаты, достигнутые разными педагогами, использующими одну и ту же технологию, будут различными, однако близкими к некоему среднему индексу, характеризующему рассматриваемую технологию.
Рассмотрим некоторые аспекты технологии обучения в коррекционной школе:
Обучение в сотрудничестве
В центре внимания личностно-ориентированных технологий находится уникальная целостная личность, которая стремится к максимальной реализации своих возможностей (самоактуализации), открыта для восприятия нового опыта, способна на осознанный и ответственный выбор в разнообразных жизненных ситуациях. Практика показывает, что вместе учиться не только легче и интереснее, но и значительно эффективнее. Главная идея обучения в сотрудничестве — учиться вместе, а не просто что-то выполнять вместе.
В сотрудничестве помимо усвоения нового материала, можно решать такие задачи обучения, как проверка выполнения домашнего задания, подготовка к контрольной работе и пр.
Технология уровневой дифференциации
Дифференцированное обучение — это форма организации учебного процесса, при которой учитель работает с группой учащихся, составленной с учетом наличия у них каких-либо значимых для учебного процесса общих качеств (гомогенная группа).
Основной идеей уровневой дифференциации является обязательность обучения и пятибалльная оценка результатов. В традиционной технологии эта идея имела отрицательные последствия: ученик все время находился в положении несправившегося. Это порождало у него комплекс неполноценности по отношению к учению, полностью исключало положительную мотивацию учебного успеха: вызывало неприязнь к предмету и к школе, а часто и фактический отказ от учения, вело к снижению уровня требований, процентомании.
Разноуровневое обучение
Такая организация учебно-воспитательного процесса, при которой каждый ученик имеет возможности овладеть учебным материалом по отдельным предметам школьной программы на разном уровне: А — базовый уровень, В — повышенный или С — углубленный, но не ниже базового, в зависимости от его способностей и индивидуальных особенностей личности, при которой за критерий оценки деятельности ученика принимаются его усилия по овладению этим материалом, творческому его применению.
Критерии отбора учащихся в тот или иной уровень:
1 — результаты тестирования на достижение уровня базовой подготовки,
2 — желание самих учащихся,
3 — рекомендации психолога.
Коллективный способ обучения
Обучение есть общение обучающих и обучаемых. Вид общения определяет и организованную форму обучения. КСО — это включение в учебный процесс естественной структуры общения между людьми — диалогических пар.
Работа начинается с ввода или так называемого «запуска» раздела. Преподаватель, работая индивидуально с каждым по очереди, объясняет, как решается задача «а» того задания, которое должен выполнить ученик. Дает теоретическую консультацию, записывает решение задачи прямо в тетрадь ученика. Задачу «б» своего задания ребята решают самостоятельно, а правильность решения проверяют у преподавателя. После проверки ученику ставится в таблице «+».
Раздел считается введенным в работу (запущенным в технологический процесс), если каждое его задание выполнено хотя бы одним учеником.
На карточках или в тетради даются по два однотипных задания. Каждое задание имеет свой номер. Пример: задание по разделу «Решение уравнений с десятичными дробями» (РУ)
Задание РУ1. Решить уравнение:
а) х + 4,5 = 11,6
б) х+ 22,7 = 37,6
Задание РУ2. Решить уравнение:
а) 33,4 — х = 13,2
б) 78,4 — х = 45,7
Организация работы учащихся
Предположим, Саша знает решение всех уравнений из задания РУ1, а Костя — их РУ2. Объединяясь в пару, они могут обменяться знаниями: Саша учит Костю решению уравнений «а» из задания РУ1; если нужно, он дает теоретические объяснения, отвечает на вопросы Кости. Записать решение уравнения он может прямо в Костину тетрадь. Затем таким же образом учит Костя, объясняя Саше, как решается уравнение «а» из задания РУ2. Потом Костя самостоятельно решает уравнение «б» из задания РУ2. Проверив друг у друга правильность решения, ребята расходятся. На этом их работа в паре заканчивается. Каждый из них ищет себе нового партнера. (Данная организация коллективной работы больше походит на элементы Сингапурской методики).
Итоговым контролем является срез знаний или тестирование по разделу: «Решение уравнений с десятичными дробями».
Построение коррекционно-педагогической деятельности с детьми и подростками, организацию дифференцированного обучения и индивидуального воспитания невозможно осуществить, не зная природы недостатка в развитии ребенка, не выяснив и не изучив причины его отклонений в поведении. Одним словом, без знаний основ общей психологии человека трудно организовать эффективную коррекционную работу, тем более что результаты исследования закономерностей психического развития ребенка показывают, что они идентичны как для нормы, так и для патологии. Вместе с тем для детей с недостатками в развитии характерны такие особенности психики, которые не всегда можно встретить у нормальных детей: задержка общего физического развития, замедленность, слабость и малоподвижность нервных процессов, неразвитость сенсорных анализаторов, неполное (фрагментарное) восприятие окружающего мира и др.
В «Педагогической энциклопедии» понятие «коррекция» определяется как исправление (частичное или полное) недостатков психического и физического развития у аномальных детей с помощью специальной системы педагогических приемов и мероприятий. Причем коррекция рассматривается как педагогическое воздействие, которое не сводится к тренировочным упражнениям, направленным на исправление (ликвидацию) отдельно взятого дефекта, а подразумевает воздействие на личность ребенка в целом.
При работе с детьми, имеющими ограниченные возможности здоровья на уроках математики, мы применяем особые коррекционно-развивающие педагогические технологии, позволяющие добиваться положительной динамики в обучении и воспитании, при этом используем нетрадиционные формы его проведения: урок-творчество, урок-игра. Не ошибемся, если скажем, что ведущим видом деятельности в коррекционной педагогике является игра. Игра — одно из замечательных явлений жизни, деятельности, как будто бесполезная и вместе с тем необходимая. В отличие от игр вообще, педагогическая, коррекционная игра обладает существенным признаком — четкого обучения и соответствующим ей педагогическим результатом, которые могут быть обоснованны в явном виде и характеризуются учебно-познавательной направленностью. Игровая форма на уроках математики создается при помощи игровых приемов и ситуаций, выступающих как средство побуждения, стимулирования к учебной деятельности. Грамотно сочетая традиционные и инновационные технологии мы обеспечиваем развитие у обучающихся, воспитанников познавательной активности, творческих способностей, школьной мотивации в учебно- воспитательном процессе.
Реализация игровых приемов и ситуаций при урочной форме занятий математикой происходит по следующим основным направлениям:
дидактическая цель ставится перед учащимися в форме игровой задачи;
учебная деятельность подчиняется правилам игры;
учебный материал используется в качестве ее средств;
в учебную деятельность вводится элемент соревнования, который переводит дидактическую задачу в игровую;
успешное выполнение дидактического задания связывается с игровым результатом.
В настоящее время проблема активизации познавательной деятельности учащихся на уроке математики отражена в новой редакции “Программы специальных (коррекционных) общеобразовательных учреждений VIII вида”, а именно “...использовать процесс обучения математике для повышения уровня общего развития учащихся вспомогательных школ и коррекции недостатков их познавательной деятельности и личностных качеств” [2, с. 29].
Урок математики для детей с проблемами в развитии является одним из труднейших, и по этой причине многие дети не любят этот предмет.
В задачи учителя входит преодоление равнодушия, умственной инерции школьника. Вы все прекрасно знаете, как важно, чтобы урок с самого начала пошёл в нужном русле. Для математики начало урока — это устный счёт. Мы не один год занимаемся этой проблемой и можем сказать, что если хорошо, интересно проведён устный счёт, то и дальше урок пойдёт успешнее, дети будут активны, заинтересованы.
А чтобы заинтересовать детей, нужно подбирать разнообразные игровые задания. Это могут быть игры вычислительного характера, разгадывание ребусов, задания на внимание, геометрические задания.
Для воспитания творческой личности на уроках закрепления и систематизации изучаемого материала можно предложить учащимся целый ряд творческих заданий.
1. Составить задачу по теме “Десятичные дроби”, “Нахождение дроби от числа”, “Нахождение числа, по заданному значению его дроби”
2. Написать математическую сказку или стихотворение;
3. Составить кроссворд;
Обучение учащихся умению их выполнять является основной частью умения применять математические знания. Кроме того, в кабинете можно организовать выставку творческих работ учеников.
Учебная занимательность дает разные результаты в зависимости от места и времени, которые она занимает в процессе обучения. Поэтому, готовясь к уроку, мы определили для себя, с какой целью привносится в урок тот или иной занимательный элемент.
Например, учащимся 5–6 классов очень нравится игра “Ай, да я”. К доске выходит несколько учеников и выстраивается в шеренгу. По очереди ребята начинают счет (когда счет доходит до конца шеренги, его продолжает ученик стоящий первым). Числа, содержащие в записи цифру «3» и “7” произносить нельзя. Играющий, который должен был назвать это число, произносит фразу: “ай, да я”. Тот из учащихся кто произнесет запрещенное число или скажет не вовремя фразу, выходит из игры, а счет начинается снова.
Игра “Эстафета”
Эта форма работы очень эффективна в начале урока, когда надо быстро перестроить мысли ребят на рабочий лад, или повторить определенную тему, или занять ребят, пока кто-нибудь из учеников выносит на доску ключевые моменты домашней работы.
Задания эстафеты могут содержать не только материал, предусмотренный школьной программой, но и дополнительный, разного уровня сложности, а также включать вопросы не математического характера (это делает эстафету более привлекательной для ребят). Задания следует подбирать с увеличением уровня сложности, чтобы создать ситуацию успеха для слабых учащихся.
Игра «Дробный мозгодром»
-
Найдите
 от 6.
от 6.
-
Найдите
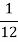 часа.
часа.
-
Было 2 килограмма конфет. На Новый год съели
 этих конфет. Сколько осталось?
этих конфет. Сколько осталось?
-
Найдите
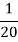 мин.
мин.
В создании интереса к учению большое значение имеют задачи-смекалки, арифметические и геометрические головоломки, задачи со сказочным сюжетом, а также задачи в стихах. Такие задания позволяют без особых усилий сконцентрировать внимание учащихся, включить весь класс в работу:
“Исключи лишнее”;
Назови число в правом верхнем углу;
Прочти число, записанное зеленым цветом;
Игра “Молчанка” — ученикам предлагается выполнять действия самостоятельно, а ответы показывать с помощью сигнальных карточек.
При проведении этих игр мы используем разработанные наглядные пособия. Это привлекает внимание учащихся к предъявленным играм, пробуждает интерес, а, следовательно, и активизирует их познавательную деятельность.
Разнообразие видов и форм устных упражнений привлекает внимание учащихся к заданиям, способствует формированию беглого счета, развивает интерес к математике, подготавливает учащихся к использованию полученных знаний по математике в повседневной жизни, при овладении профессией. Упражнения, выполняемые в классе, образуют определенную систему. Их цель не только закрепление изучаемого материала, но и формирование вводимых понятий, установление связи между вновь вводимыми и ранее изученными понятиями, развитие логического мышления:
Занимательные квадраты:
а) Определить сумму по диагонали;
б) Определить каждое число (заполнить все клетки).
Слуховой диктант. У учащихся трафареты геометрических фигур. Называются фигуры, учащиеся обводят данные фигуры в той последовательности, как они были названы.
Конфуций писал: «Учитель и ученик растут вместе». Игровые формы уроков позволяют расти как ученикам, так и учителю.
Как известно, у школьников со сложностями в обучении математики зачастую развитие мышления, памяти, внимания, восприятия, речи, эмоционально-волевой сферы личности зачастую происходит замедленно с отставанием от нормы; ведущей остается игровая мотивация, с трудом формируются учебные интересы; слабо развитая произвольная сфера: умение сосредотачиваться, переключать внимание, усидчивость, умение удерживать задание, работать по образцу; для детей типичны дезадаптивные формы поведения возбудимого или заторможенного характера.
Труд рабочих даже самых простых профессий требует умения обращаться с компьютерной техникой, разбираться в чертежах, спецификациях, умения самостоятельно производить расчеты, принимать самостоятельные решения. В связи с этим очевидно, что уроки математики в коррекционной школе должны носить глубокую практическую направленность. Включение в урок задач, содержание которых взято из жизни, позволяет расширить кругозор обучающихся, вести активную коррекционную работу на уроках. В таких условиях становится актуальным требование тесной связи обучения математике с профессионально — трудовым обучением, так как последнее занимает значительное место в учебном процессе коррекционной школы.
При изучении геометрического материала мы показываем учащимся на конкретных, доступных примерах, что знание мер, умение делать устные вычисления, решать задачи, производить измерения, помогут им успешнее сделать чертежи, разметки на уроках труда. А знание свойств геометрических фигур (квадрата, прямоугольника, треугольника) поможет в практической работе над столярными или швейными изделиями (при раскрое ткани).
Полезным является и составление задач, числовые данные для которых учащиеся добывают сами (например: цены на продукты и товары первой необходимости). При этом расширяется запас представлений умственно отсталых детей об окружающем мире, обогащается их жизненный опыт.
В последнее время школа обратила серьезное внимание на экономическое воспитание школьников. Процесс формирования экономических знаний в коррекционных школах идет очень медленно, хотя, как показывает опыт работы, многие умственно отсталые школьники способны усвоить некоторые экономические знания. Поэтому в практику поведения уроков математики мы широко включаем задачи, построенные по принципу простого экономического или хозяйственного расчета, повышению самостоятельности учеников путем работы по алгоритму, систематическому повышению трудности решаемых задач.
В качестве примеров можно привести следующие задания, применяемые в практической работе:
- «Минимальный месячный набор продуктов питания стоит 4500 рублей. Вы зарабатываете 8000 рублей. Сколько необходимо вам денег дополнительно для существования, если за квартиру вы платите 2 500 рублей, а за ремонт одежды и обуви 400 рублей?»
- «Мама получает 6 000 рублей в месяц, а папа 9000 рублей. В семье 3 человека. Сколько рублей в месяц в среднем приходится на каждого члена семьи? Прожиточный минимум составляет 4 350 рублей. Достаточно ли денег для проживания этой семьи?» (7 класс, тема «Среднее арифметическое»).
Предложенные задачи на наш взгляд формируют у учащихся экономическое мышление. При их решении происходит обучение элементарным расчетам, оценивается сравнительная выгода той или иной покупки, сделки. Вывод: практическая направленность преподавания математики в коррекционной школе, связь ее с производительным трудом, использование межпредметных связей, способствуют тому, что знания, полезные для жизненной практики и профессиональной деятельности, усваиваются учениками лучше и прочнее.
Обобщая используемые возможности жизненно практической ориентации, можно выделить 3 направления работы:
- Используя реальные ситуации школьной жизни, доводить до сознания школьников с ОВЗ включенные в них математические требования, стимулировать учащихся реально — практические выполнять эти требования.
- «Впускать жизнь в школу» — т. е. имитировать реальные жизненные ситуации в классе, решать возникающие в этих ситуациях задачи.
- Выносить школьные знания в реальную жизнь — т. е. решать жизненно-практические задачи в реальных жизненных ситуациях.
Уроки математики, на наш взгляд, играют также большую роль в системе реабилитационных мероприятий, направленных на решение основной задачи коррекционной школы. Совокупность образовательных, воспитательных, коррекционных мероприятий, а также комплексное воздействие школы, семьи на личность учащихся коррекционных школ является наиболее эффективным фактором, влияющим на социальную адаптацию и реабилитацию учащихся специальных (коррекционных) школ VIII вида, а также подготовки их к самостоятельной жизни и труду.
Овладение учащимися системой доступных математических знаний, умений и навыков, необходимых в повседневной жизни и в будущей профессии, так прочно, чтобы они стали достоянием учащихся на всю жизнь является на данный момент главной общеобразовательной задачей обучения математике в коррекционной школе.
Литература:
- М. В. Буланова-Топоркова, А. В. Духавнева. Педагогические технологии //учебное пособие для студентов педагогических специальностей. — Ростов-на Дону: Издательский центр «МарТ».-2010-с.5–7,35–36,50
- Т. Г. Никуленко, С. И. Самыгин. Коррекционная педагогика //учебное пособие,2-е издание., серия «высшее образование». — Ростов-на Дону: Издательский центр «Феникс».-2009.-с.364–370
- Перова М. Н. Методика преподавания математики во вспомогательной школе. — М.: Владос, 2008.
- Программа специальных общеобразовательных школ VIII вида. — М.: Владос, 2000.
- Гринько Л. А. Научно-методический журнал.//Дефектология. — 1993.–№ 2.
- Перова М. Н. Дидактические игры и упражнения по математике. — М.: Просвещение, 1996.

