Научно-технический прогресс вызывает усиление роли теоретических знаний и умственного труда различных областях человеческой деятельности. От образованного человека, от специалиста, от работника практически любой области требуется не только (и не столько) знание того, что было им ранее изучено, но и умение владеть общими идеями и понятиями и с этих позиций осмысливать новые факты, связи, идеи, обобщать результаты наблюдений, отделять существенное от несущественного и т. д. Эти качества могут быть приобретены учащимися при соответствующей организации учебного процесса, направленного на развитие творческих способностей молодого поколения.
Важную роль в развитии и реализации творческих способностей учащихся играет научно-исследовательская деятельность. Научно-исследовательская деятельность способствует формированию у учащихся таких навыков, как [1–2]:
1. умение вести практическую деятельность, т. е. умение правильно поставить цель своей работы, умение правильно планировать свои действия для достижения поставленной цели, анализ полученных данных и оценка своей работы;
2. умение правильно выдвигать гипотезы, формулировать проблемы, поиск аргументов;
3. развитие творческого мышления;
4. стремление к достижению цели, организованность, собранность при неординарных ситуациях.
Целью организации научно-исследовательской деятельности с учащимися в НИШ ХБН г. Караганды является создание условий для развития творческой личности, её самоопределения и самореализации.
В качестве примера рассмотрим, как можно организовать исследовательскую деятельность учащихся на уроке при изучении темы «Геометрическая прогрессия».
Цель урока: дать понятие геометрической прогрессии как числовой последовательности особого вида.
Предварительные знания. Учащиеся знают следующие понятия и свойства — последовательность, n-й член последовательности, способы задания последовательности (аналитический, рекуррентный, словесный и графический), прогрессия, арифметическая прогрессия и ее основные свойства.
Ход урока. Существуют различные способы введения понятия «геометрическая прогрессия». Традиционно на уроке сразу выдается определение рассматриваемого понятия. Иногда, перед тем, как объявить тему, учащимся предлагается несколько примеров геометрической прогрессии, с помощью которых учащиеся должны установить закономерность и дать определение прогрессии самим и т. д. Предлагается следующий вариант введения понятия «геометрическая прогрессия», который позволит учащимся не только самостоятельно прийти к определениям и свойствам прогрессии, но и создаст условия для развития исследовательских навыков и критического мышления. В момент, когда учащиеся знают определение арифметической прогрессии, ее основные свойства, понимают, что из определения следует, что прогрессия основана на арифметических действиях суммы или разности, в зависимости от значения шага прогрессии, учитель может задать следующий вопрос:
Существует ли прогрессия, которая основана на других арифметических действиях?
Данный вопрос учащиеся могут обсудить в группах или в парах. Исследование данной гипотезы можно разделить на три этапа.
Первый этап — это этап выявления уже имеющихся знаний и сбор необходимой информации, которые помогут изучить данный вопрос. При проведении данного этапа учитель может задавать ученикам следующие вопросы.
1. Что вы можете сказать по этому вопросу?
2. Что вы читали (слышали, изучали на предыдущих уроках, самостоятельно) по этой теме (темам), затрагивающий этот вопрос?
3. На каких арифметических действиях основана известная вам прогрессия?
4. Что, по-вашему, необходимо сделать, чтобы выявить нужную нам закономерность и определить прогрессию?
5. Что еще вы бы хотели изучить (понять), чтобы найти способ решения этой проблемы?
Следующий этап — обработка информации. На данном этапе учащиеся должны проанализировать структуру построения арифметической прогрессии. Для этого учащимся предлагается заполнить следующую таблицу.
Таблица 1
Таблица с предполагаемыми ответами учащихся по теме «Арифметическая прогрессия»
|
Арифметическая прогрессия | |
|
Описание закономерности |
|
|
Ограничение значения первого члена |
нет, |
|
Ограничение значения шага прогрессии |
есть, |
На следующем этапе — обобщение информации — учащиеся должны заполнить аналогичную таблицу. Информация, данной таблицы поможет ответить на исследуемый вопрос. Приведем предполагаемые ответы учащихся в следующей таблице.
Таблица 2
Таблица с предполагаемыми ответами учащихся на этапе обобщение информации
|
Искомая прогрессия | |
|
Описание закономерности |
для того, чтобы получить следующий член прогрессии нужно умножить (либо разделить) на число (шаг прогрессии) предыдущий член |
|
Ограничение значения первого члена |
Ограниченность есть, значение первого члена не равно нулю, в противном случае получится постоянная последовательность |
|
Ограничение значения шага прогрессии |
значение шага не равно нулю и не равно единице, в противном случае получится постоянная последовательность |
При изучении данного вопроса учащиеся:
- самостоятельно выявят закономерность;
- используя определение арифметической прогрессии, сформулируют определение рассматриваемой (геометрической) прогрессии;
- попробуют назвать ее отдельным термином, проявляя свои творческие навыки и т. д.
Таким образом, одновременно с изучением программного материала ведется работа по развитию у учащихся таких навыков, как самостоятельность, умение выдвигать свою точку зрения, развитие творческих и исследовательских навыков.
Один из важных моментов в изучении арифметической и геометрической прогрессий — это их характеристические свойства. Для выведения характеристического свойства можно использовать аналогию — метод исследования, основанный на изучении сходства или различий по ряду признаков предмета исследования и его аналога.
Характеристическое свойство арифметической прогрессии: каждый ее член, кроме первого, равен полусумме двух соседних с ним членов, т. е., если 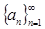 — арифметическая прогрессия, то для любого натурального
— арифметическая прогрессия, то для любого натурального 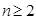 выполняется формула:
выполняется формула:
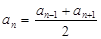 .
.
Преобразуем эту формулу.
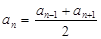
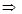
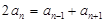 или
или 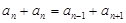
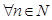 ,
, 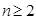 .
.
Последнее равенство говорит о том, что если сложить любой член арифметической прогрессии, начиная со второго, с самим собой, то получим сумму, равную сумме соседних двух членов.
Учащимся дается задание установить аналогичное свойство, которое будет выполняться только для геометрической прогрессии.
Из вышеуказанного учащиеся могут сделать правильное предположение:
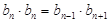
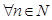 ,
, 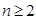
и вывести характеристическое свойство геометрической прогрессии.
Достаточно только использовать определение геометрической прогрессии и истинность данной формулы будет доказана.
Подобная организация исследовательской деятельности на уроках способствуют развитию умения учащихся заниматься научно-исследовательскими проектами, как на уроке, так и вне урока. Речь идет об одаренных детях. Для таких учащихся можно предложить исследовать следующую гипотезу.
Если арифметическая и геометрическая прогрессии основаны на арифметических действиях суммы (разности) и умножения (деления), то существует прогрессия, которая основана на действии возведение в степень число.
Данное исследование было проведено учащимися нашей школы. Изучая данный вопрос, учащиеся провели следующее построение искомой последовательности. Возьмем любое положительное действительное число, отличное от единицы, и возведем ее в некоторую положительную степень, не являющейся нулем и единицей. Полученное число снова возведем в ту же степень и т. д. Тогда полученные числа образуют новую прогрессию, которую назвали показательной. Например, следующая последовательность является показательной:
2, 4, 16, 256, 65536, ….
Результатом данной деятельности стал проект на тему «Показательная прогрессия и некоторые ее свойства». Цель проекта — определение нового вида прогрессии и доказательство некоторых ее свойств. Данная тема относится к разряду долгосрочных проектов, т. е. для достижения поставленной цели понадобиться несколько уроков, а также несколько дополнительных занятий.
Почему именно показательная прогрессия? Так как члены рассматриваемой прогрессии являются степенями и в них изменяются лишь показатели, было решено назвать данную числовую последовательность показательной прогрессией.
После того как была определена данная прогрессия, был поставлен вопрос о ее свойствах таких, как вывод общей формулы n-го члена, характеристического свойства и т. д. Формула n-го члена определяется и доказывается аналогичным способом как в арифметической и геометрической прогрессиях.
Изучая характеристические свойства арифметической и геометрической прогрессий, можно предположить, что характеристическое свойство показательной прогрессии будет связано со следующим равенством:
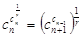 , для любого
, для любого 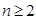 .
.
В данном проекте также доказаны небольшие теоремы, описывающие связь между рассматриваемой прогрессией и арифметической и геометрической прогрессиях.
Исследовательская деятельность на уроках математики — это прекрасное средство повышения учебной мотивации, творческого, личностного развития учащегося и формирование мировоззрения и компетенций через сотрудничество учителя и ученика.
Литература:
1. Арцев М. Н. Учебно-исследовательская работа учащихся // Завуч. — 2005. № 6. — С.4–29.
2. Барсуков, М. А. Ресурс образовательного процесса — проектная и исследовательская деятельность учащихся в дополнительном образовании // Исследовательская работа школьников. — 2008. — N 3. — С.113–117.
3. Сергеев И. Н., Олехник С. Н., Гашков С. Б. Примени математику. — М.: Наука. Гл. ред. Физ.-мат. лит., 1989. — С240
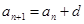 , для того, чтобы получить следующий член прогрессии нужно прибавить (либо отнять) число (шаг прогрессии) к предыдущему члену
, для того, чтобы получить следующий член прогрессии нужно прибавить (либо отнять) число (шаг прогрессии) к предыдущему члену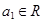 , любое значение
, любое значение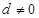 , значение шага не равно нулю, в противном случае получится постоянная последовательность
, значение шага не равно нулю, в противном случае получится постоянная последовательность
