В современном мире интеллектуальный и творческий потенциал подрастающего поколения любой страны можно рассматривать как основной её капитал. В связи с этим, работа с одаренными детьми является одним из приоритетных направлений в современном образовании.
Согласно теории психолога Дж.Рензулли, одаренность есть сочетание трех основных характеристик: интеллектуальных способностей (превышающих средний уровень), креативности и настойчивости (мотивация, ориентированная на задачу). [1] Разработанная Дж.Рензулли концепция предполагает, что контингент одаренных детей может быть значительно шире, чем при их идентификации по тестам интеллекта, креативности или достижений. Автор предлагает относить к категории одаренных тех детей, кто проявил высокие показатели хотя бы по одному из параметров.
Характерными чертами одаренного учащегося является повышенная познавательная деятельность, а также готовность по собственной инициативе выходить за пределы изучаемого. Эти дети критически оценивают любую информацию, не принимают стандартных, типичных заданий и готовых ответов. Признаки одаренности связаны с высоким уровнем выполнения деятельности. Такой ребенок стремиться завершить начатое дело. Причем он, не просто, выполняет задания, а создает что-то новое, меняет привычное. Он часто критичен к результатам своего труда, стремится к постоянному поиску.
Главной задачей современного учителя является создание благоприятных условий для развития одаренных детей через применение различных средств, форм и методов в урочное и внеурочное время.
Одним из эффективных подходов, способствующих развитию одаренности учащихся, наряду с дифференцированным обучением является проблемное обучение, которое обеспечивает организацию самостоятельной поисково-исследовательской деятельности учащихся. В дидактике Скаткиным М. Н. и в теории обучения математике В. И. Крупич установлено, что основой проблемного обучения являются проблемно-поисковые задачи, в процессе решения которых развивается исследовательская активность, формируются творческие умения учащихся. [2], [3]
Следует отметить, что любую математическую задачу можно рассматривать как проблему, но не каждая задача наталкивает учащихся на проблемно-поисковую деятельность. Лишь те задания, которые сформулированны особым образом, т. е. в проблемно-поисковом контексте, очень эффективны в развитии нестандартного мышления учащихся, так как при решении таких задач, необходимо сначала найти проблему, затем выполнить поиск и предложить варианты её решения, обосновывая свой ответ.
Например, при изучении темы «Нахождение наименьшего и наибольшего значения функции», предлагая учащимся решить следующую задачу: «Найдите наибольшее значение функции ![]() на отрезке [1;4]», в качестве результата можно получить лишь отработку навыка применения известного алгоритма. Этот тип задания необходимо применять на первых этапах изучения темы, так как в таких типичных заданиях проблема сформулирована очевидна и не требует дополнительных исследований.
на отрезке [1;4]», в качестве результата можно получить лишь отработку навыка применения известного алгоритма. Этот тип задания необходимо применять на первых этапах изучения темы, так как в таких типичных заданиях проблема сформулирована очевидна и не требует дополнительных исследований.
В рамках изучения этой же темы, учащимся полезно предложить следующую прикладную задачу: «В гостинице имеются два коридора шириной 4 м и 3 м. Они пересекаются под прямым углом. (см. рис. 1) Какой максимальной длины зеркало можно пронести по этим коридорам? Обоснуйте свой ответ».
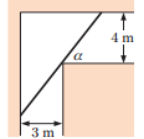
Рис. 1.
При решении данной задачи учащиеся сначала высказывают свои предположения о том, от чего зависит длина зеркала, затем составляют функцию, выражающую длину зеркала. Далее делают вывод о том, что при наименьшем значении ![]() , длина зеркала достигает наибольшего значения, обосновывая свой ответ через применение производной.
, длина зеркала достигает наибольшего значения, обосновывая свой ответ через применение производной.
Решение нестандартных задач на уроках математики дает возможность учителю создать условия для творческого применения знаний одаренными обучающимися. Работа может выстраиваться индивидуально или в группах однородного состава. Учитель предлагает классу перечень задач. Каждый учащийся самостоятельно выбирает какие задачи ему решать: типовые или нестандартные. Как показывает практика, одаренные дети всегда выбирают нестандартные задания.
Например, при изучении раздела «Объем многогранников и тел вращения» учащиеся с удовольствием решат следующую задачу: «36 солдат, находящихся на полевых сборах, размещены в палатке (см.рис.2). На каждого солдата приходится 11 ![]() воздуха в палатке. Найдите размеры палатки, если кровать каждого солдата занимает площадь 4
воздуха в палатке. Найдите размеры палатки, если кровать каждого солдата занимает площадь 4 ![]() . Какой можно сделать вывод об условиях размещения солдат? Ответ обоснуйте.
. Какой можно сделать вывод об условиях размещения солдат? Ответ обоснуйте.
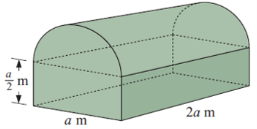
Рис. 2.
Предложенная задача ориентирована на видение проблемы, перенос знаний и умений в новую ситуацию, на комбинирование известных методов решения, при выполнении которых учащийся должен «открыть» подлежащие усвоению новые знания и действия. При этом ответ к задаче для учащихся окажется особо неожиданным, так как они сделают вывод о том, что солдаты размещены в палатку с двухъярусными кроватями.
Учитель также может предложить учащимся проблемно-поисковую задачу, столкнув их с противоречиями в ходе практической деятельности. Так, при изучении темы «Неравенство треугольника», до введения основной теоремы учащимся можно предложить задачу: «Построить треугольник со сторонами равными: а) 4см, 5см, 6см; б) 2см, 3см, 6см; в) 3см, 4см, 7см. В ходе решения и при последующем обсуждении учащиеся приходят к тому, что не всегда можно построить треугольник из трёх отрезков.
Решение таких задач в формате повторного открытия, а не простой передачи готовых знаний, приносят радость открытия, веру в себя, дает возможность одаренным детям работать на самом высоком уровне.
Учитель также может побуждать учащихся проводить аналогию с ранее изученным материалом. Например, повторяя тему «Арифметическая и геометрическая прогрессии», учащимся была сформулирована проблемно-поисковая задача: «Существует ли последовательность, обобщающая арифметическую и геометрическую прогрессии, т. е. сочетающая их свойства и признаки?» Этот вопрос побудил целый ряд проблемно-поисковых задач и натолкнул некоторых учащихся к самостоятельному исследованию, успешному написанию проектной работы и научной статьи, что несомненно является показателем их одаренности. Учащиеся по аналогии с ранее изученным материалом построили целую теорию арифметико-геометрической прогрессии.
Также полезно предложить учащимся одну задачу, которую можно решить различными методами. Это создаст условия для организации групповой учебно-исследовательской деятельности, развитию мышления учащихся. Группы лучше организовать смешанные, ведущая роль в которой отведена одаренному учащемуся. Например, рассматривается общеизвестная задача «Докажите, что средняя линия трапеции параллельна основаниям и равна их полусумме». Ее можно решить, как минимум пятью способами:
Решение 1. Пусть ABCD — данная трапеция, E и F — середины боковых сторон AD и ВС. Проведите прямую DF. Точку пересечения прямых DF и АВ обозначьте через К. Докажите, что EF — средняя линия треугольника АDК.
Решение 2. Середину М диагонали АС трапеции соедините с точками E и F. Примените свойство средней линии треугольника.
Решение 3. Через вершину С трапеции проведите прямую, параллельную стороне AD.
Решение 4. Через середину F стороны ВС трапеции проведите прямую, параллельную стороне AD.
Решение 5. Воспользуйтесь векторным равенством ![]() . [4]
. [4]
Сначала можно записать все идеи решения задачи, предложенные учащимися, при необходимости дополнив их ответы. Затем объединить учащихся в несколько творческих групп, каждая из которых решает задачу выбранным способом и на этапе защиты предоставляет полное решение. Следует отметить, что одаренные дети отдают предпочтение таким задачам и стремятся рассмотреть самостоятельно все способы решения.
Критически мыслить учащихся наталкивают проблемно-поисковые задачи с недостаточными или избыточными данными, с неопределённостью в постановке вопроса, с противоречивыми данными, заведомо допущенными ошибками. Например, в рамках изучения комбинаторики и теории вероятностей можно предложить ряд интересных нестандартных задач такого типа, одна из которых представлена ниже.
«На уроке была предложена задача: «У Вани есть 6 учебников по разным предметам, один из которых учебник алгебры. Он наугад кладет в портфель два учебника. Какова вероятность того, что один из них окажется учебником алгебры?
Школьник предложил такое решение: «Если Ваня положит в портфель только один учебник, то вероятность того, что это будет учебник алгебры, равна ![]() . А так как он кладет два учебника, то вероятность удваивается, следовательно, она равна
. А так как он кладет два учебника, то вероятность удваивается, следовательно, она равна ![]() .
.
Разгорелся спор. Одни считали предложенное решение, в целом, верным, хотя и недостаточно обоснованным. Другие утверждали, что решение ошибочно, хотя и приводит к верному ответу. На чьей Вы стороне и почему? Приведите еще пару примеров задач по комбинаторике или теории вероятностей, в которых верный ответ получается путем неверных или неполных рассуждений. Объясните, из каких соображений можно либо опровергнуть каждое из приведенных Вами «решений», либо довести его до верного». [5]
Данная задача поможет учащимся по-новому «взглянуть» на ранее ими изученное. Заставит осмыслить многие правила и законы комбинаторики и теории вероятностей, а также способствует развитию комбинаторного мышления учащихся, научит их критически оценивать различные суждения.
Исследования и практика показывают, что одаренные дети отличаются познавательной активностью. Они хотят учиться и добиваться успехов. Обучение доставляет им радость, они приобретают знания с большим удовольствием. Главной целью учителя является способствование развитию мыслительной деятельности учащихся, повышению познавательной активности и развитию их одаренности в процессе овладения знаниями.
Основным инструментом для достижения этой цели на уроках математики были и остаются проблемно-поисковые задачи, в ходе решения которых обучающиеся осваивают структуру учебного исследования: постановка проблемы, выдвижение гипотезы, проверка гипотезы, вывод; а также этапы его проведения: постановка проблемы исследования, анализ имеющейся информации по рассматриваемому вопросу, экспериментирование (проведение измерений, проб и т. д.), систематизация и анализ полученного фактического материала, выдвижение гипотезы, подтверждение или опровержение гипотезы.
Литература:
- Рензулли Дж.С., Рис С. М. Модель обогащенного школьного обучения: практическая программа стимулирования одаренных детей //Современные концепции одаренности и творчества /Под ред. Д. Б. Богоявленской. М., 1997.
- Скаткин М. Н. Проблемы современной дидактики. 2 –е изд. -- М.: Педагогика, 1984. — 96 с. (Воспитание и обучение. Б-ка учителя)
- Крупич В. И. Структура и логика процесса обучения математике в средней школе: Метод. разраб. по спецкурсу для слушателей ФПК. М.: МГПУ, 1985. 118 с.
- Готман Э. Г., Скопец З. А. Задача одна решения разные. Киев: Радянська школа, 1988. 174 с.
- https://www.mccme.ru/oluch/Zaoch_14_usl.htm (IX заочный тур творческого конкурса учителей)

