Использование проблемного обучения для активизации познавательной деятельности учащихся

Создание проблемной ситуации является началом мыслительного процесса. Когда у человека появляется потребность что-то понять, он начинает мыслить. Возникновение проблемы или вопроса, которые вызывают удивление, недоумение, противоречие, даёт толчок для вовлечения личности в мыслительный процесс. Одним из важных компонентов современной модели школьного образования является ориентация на практические навыки, на способность применять знания, реализовывать собственные проекты, уметь ориентироваться в любой ситуации и находить пути решения любой проблемы. Для того чтобы научить ребёнка решать жизненные задачи недостаточно одностороннего изучения готовой информации. Необходимо использовать на уроках такие способы, которые побуждали бы учеников к непосредственному познанию действительности, к самостоятельному разрешению теоретических проблем, то есть к мыслительной деятельности. Одним из таких способов, направленных на достижение такой мыслительной деятельности, и является проблемное обучение. Суть проблемного обучения состоит в том, что учитель не сообщает знания в готовом виде, а ставит перед учащимися проблемные задачи, заставляя их искать пути и средства решения. Это наиболее эффективное средство активизации мышления ученика. Для этого ученик должен научиться анализировать фактический материал и оперировать им так, чтобы самому получить из него новую информацию. Учитель не даёт нового применения прежних знаний, оно ищется и находится учеником, поставленным в соответствующую ситуацию. Одним из методов проблемного обучения является исследовательский, где учитель организует самостоятельную работу учащихся по изучению нового материала, предлагая им задания проблемного характера и разрабатывая совместно с ними цель и ход работы. Проблемные ситуации, как правило, возникают в ходе выполнения учащимися заданий, имеющих обычно не только теоретический, но и практический характер. На уроках математики созданием проблемной ситуации может служить решение «ключевых задач». Эти задачи можно использовать как при переходе от теории к практике, так и решение конкретной задачи подводит учащихся к необходимости рассмотреть новый теоритический материал. «Ключевые задачи» — это опора для решения других математических задач. Если учащиеся смогут овладеть методами решения «ключевых задач», то они решат любую задачу, разбив её на части. Где каждая часть — это тоже «ключевая задача». К решению таких задач приводит метод проб и ошибок. Эти поисковые пробы решения приводят к догадкам, которые представляют собой нахождение пути выхода из проблемной ситуации заданной этой задачей. Возникновение догадок говорит о том, что у детей развиваются такие качества умственной деятельности, как смекалка и сообразительность. Это заключается в умение обдумывать данную ситуацию, устанавливать взаимосвязи, приходить к выводам, обобщениям, умению оперировать знаниями. Такие качества умственной деятельности и надо развивать в процессе обучения. Решая «ключевые задачи» учителю необходимо направлять познавательную деятельность школьников. Учитель формулирует условие разбираемой задачи, далее совместно с учениками выбирается тот или иной подход к решению. Может быть, что выбранный путь не приводит к нужному решению. Возникшая ситуация учит учащихся гибкости мышления, умению отказываться от выбранного метода решения, переключению на другую идею. Использование «ключевых задач» в роли проблемной ситуации на уроке позволяют добиться решения двух целей: развитие мышления и творческих возможностей каждого ученика и умения решать математические задачи. Рассмотрим «ключевую задачу»: пусть ABCD — трапеция, M и N — середины оснований AB и CD, P=AN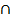DM, Q = CM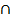BN. Доказать, что площадь четырёхугольника MQNP равна сумме площадей треугольников ADP и BCQ. Обобщить задачу. В ходе решения задачи учащиеся предложили провести отрезок MN. Получили два четырёхугольника AMND и BCNM. Используя теоритический материал, ученики приходят к решению задачи. Ну тут возникает проблема: учитель предлагает найти ошибку в решении задачи. В ходе рассуждения выясняется, учащиеся ошибочно утверждали, что оба четырёхугольника AMND и BCNM являются трапециями. Уроки, где используются проблемные ситуации, проходят интереснее, эмоциональнее, вырабатывается потребность анализировать, доказывать, спорить. А в спорах рождается истина. Приведём пример использования проблемной ситуации на уроках истории. При изучении темы «Освоение Западной Сибири в XVI веке» возникла проблемная ситуация: чем являлось освоение Западной Сибири — колониальным захватом её территории и насильственным порабощением проживающего на ней коренного населения или мирным освоением новых территорий и защитой государства от набегов хана Кучума. Анализируя исторические события, сопоставляя различные мнения, учащиеся делают собственные выводы, аргументированно отстаивают собственную точку зрения пытаясь решить историческую проблему: «Кто же Ермак со товарищами — завоеватель или освободитель?» Приводятся доказательства «за» и «против».

Завоеватель:

1.                  Северные монголы и татары не умели пользоваться изобретением пороха в конце XVI века, а казаки использовали огнестрельное оружие. Значит, на их стороне было преимущество.

2.                  За покорение Сибири Ермаку царём дарован титул «князь Сибирский». Поэтому Ермак имел личную выгоду из этого похода.

3.                  После присоединения к Российскому государству сибирские народы должны были платить дань — ясак.

Освободитель:

1.                  Этим походом Ермак обезопасил русские границы от нападения хана Кучума.

2.                  Коренным народам насаждалось мусульманство и сибирскому хану они платили ясак.

3.                  В эпосе сибирских народов, в русской литературе Ермак и казаки воспеваются как герои.

4.                  Западная Сибирь благодаря походу Ермака получила своё развитие. Были построены города.

Ученики делают вывод, что нельзя считать поход Ермака колониальным завоеванием Сибири, а его завоевателем. Можно сделать вывод: если знания добыты самостоятельно, то они удерживаются сознанием дольше, чем те, что получены в готовом виде. На уроках проблемную ситуацию можно использовать при следующих условиях:

1.                  Учащиеся должны обладать определённым минимумом знаний.

2.                  Активная познавательная деятельность у детей.

3.                  Очень хорошая эмоциональная атмосфера на уроке.

По мнению В. Оконь: «Решение учащимися проблемы, имеет огромное преимущество перед простым заучиванием готовой информации. Преимущество заключается в том, что при решении проблемы учащийся активно мыслит. А это приводит не только к прочности и глубине знаний, приобретенных самостоятельно, но и к ценнейшему качеству ума — умению ориентироваться в любой ситуации и самостоятельно находить пути решения любой проблемы». Основной целью проблемного обучения является создание условий, при которых учащиеся открывают новые знания, овладевают новыми способами поиска информации, развивают проблемное мышление. Используются различные формы продуктивной деятельности учащихся и их самоорганизации в процессе обучения. В связи с этим учитель призван действовать, как партнёр, организатор деятельности учащихся, консультант, но не служить источником новых знаний. Учитель должен чувствовать проблемную ситуацию и уметь ставить понятные для учеников реальные учебные задачи. На сегодняшний день все новые подходы и методы обучения, по сути, сводятся к одному — поиску таких форм организации занятий, в которых учащийся мог бы максимально проявить свои способности, овладеть соответствующими компетенциями в условиях самостоятельной работы. Использование проблемного обучения создаёт условия для учащихся, где им необходимо проанализировать, понять ситуацию, сформулировать проблемы и наметить пути и способы их решения. Кроме того, важной положительной стороной проблемного обучения является развивающий характер.

Литература:

1.                  Иванов Д. А. Компетентности и компетентностный подход в современном образовании — М.:НОУ Центр «Педагогический поиск». Научно-практический журнал для администрации школ. Управление современной школой. Завуч. 2008, № 1.- 144с.

2.                  Зимняя И. А. Компетентность человека — новое качество результата образования. http://www.bigpi.biysk.ru/wwwsite/source/no/barnaul/material-barnaul/aktual-vopros/2–3/kniga_2/knig_2.doc

3.                  Кудрявцева Н. Г. Проектная деятельность учащихся -М.: Информационный центр «Ресурсы образования». Справочник заместителя директора школы. 2008, № 8–110с.

4.                  Кудрявцев В. Т. Проблемное обучение: истоки, сущность, перспективы. — М.: «Знание», 1991. — 80с.

5.                  Лернер И. Я. Проблемное обучение. — М.: «Знание», 1974. — 64с.

6.                  Матюшкин А. М. Актуальные вопросы проблемного обучения. — М.: «Просвещение», 1968. -203с.

7.                  Махмутов М. И. Организация проблемного обучения в школе. Книга для учителей. — М.: «Просвещение», 1977. — 240с.

8.                  Оконь В. Основы проблемного обучения. Пер. с польск. — М.: «Просвещение», 1968. — 208с.

9.                  Полтавская Г. Б. Математика. 5 -11 классы: проблемно — развивающиеся задания, конспекты уроков, проекты. — Волгоград: Учитель, 2010. — 143 с.