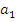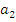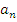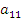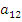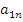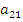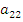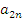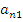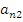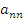В статье рассматривается вопрос об определении свойств бинарной операции (в частности, ассоциативность) некоторой конечной алгебры, заданной таблицей Кэли.
Ключевые слова: алгебра, таблица Кэли, тест ассоциативности.
The article discusses the issue of determining the properties of binary operations (in particular, associativity) of some finite algebra given by the Cayley table.
Keywords: algebra, Cayley table, test of associativity
В данной статье рассмотрим вопрос, касающийся свойств бинарной операции некоторой конечной алгебры [4], заданной так называемой таблицей Кэли [1, 3]. По этой таблице требуется определить, ассоциативна ли данная бинарная операция или нет. Для определения ассоциативности бинарной операции можно воспользоваться тестом ассоциативности по Лайту [3]. В дальнейшем покажем, как работает данный метод.
Рассмотрим алгебру с одной бинарной операцией 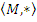 . Такую алгебру называют группоидом [2, 3].
. Такую алгебру называют группоидом [2, 3].
Помимо замкнутости (то есть отображения 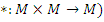 группоид может обладать и другими свойствами, например (в скобках указаны принятые названия полученных алгебр):
группоид может обладать и другими свойствами, например (в скобках указаны принятые названия полученных алгебр):
- наличие симметричных элементов (квазигруппа);
- наличие нейтрального и симметричных элементов (лупа);
- ассоциативность (полугруппа);
- ассоциативность с нейтральным элементом (моноид);
- ассоциативность с нейтральным и симметричными элементами (группа или ассоциативная петля);
- коммутативность, ассоциативность с нейтральным и симметричными элементами (абелева группа) [1, 4].
Пусть дана полугруппа 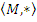 . Сформулируем теорему, которая обобщает закон ассоциативности. Суть этого обобщенного закона в том, что если рассмотреть композицию любой конечной последовательности элементов полугруппы, то скобки в выражении можно расставлять любым образом или вовсе их убрать, то есть, например, будет иметь место:
. Сформулируем теорему, которая обобщает закон ассоциативности. Суть этого обобщенного закона в том, что если рассмотреть композицию любой конечной последовательности элементов полугруппы, то скобки в выражении можно расставлять любым образом или вовсе их убрать, то есть, например, будет иметь место: 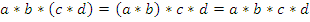 и т. д.
и т. д.
Теорема: Пусть 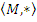 — полугруппа и
— полугруппа и  — последовательность элементов из
— последовательность элементов из 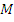 . Пусть
. Пусть 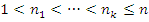 , где
, где 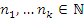 , и
, и 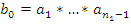 ,
, 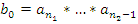 ,…,
,…, 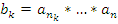 , тогда
, тогда 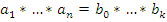 [4].
[4].
Таблица Кэли [1, 3] — это таблица, которая используется для описания структуры конечного группоида 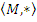 . Пусть
. Пусть 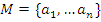 , тогда таблица Кэли имеет следующий вид (таблица 1):
, тогда таблица Кэли имеет следующий вид (таблица 1):
Таблица 1
|
* |
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
... |
… |
|
|
|
|
… |
|
Где на пересечении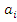 -строки и
-строки и 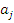 -столбца находится элемент
-столбца находится элемент 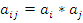 . При этом следует иметь ввиду, что в общем случае
. При этом следует иметь ввиду, что в общем случае 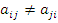 , так как свойство коммутативности бинарной операции группоида не требуется.
, так как свойство коммутативности бинарной операции группоида не требуется.
Таблицы Кэли впервые появились в статье Кэли «On The Theory of Groups, as depending on the symbolic equation 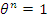 " [5] в 1854 году. В этой статье это были просто таблицы, используемые в иллюстративных целях. Называть таблицами Кэли их стали позже в честь их создателя.
" [5] в 1854 году. В этой статье это были просто таблицы, используемые в иллюстративных целях. Называть таблицами Кэли их стали позже в честь их создателя.
По таблице Кэли можно определить коммутативность, ассоциативность, идемпотентность бинарной операции и минимальное порождающее множество конечного группоида. А также нейтральный, обратимые, симметричные элементы и идемпотенты.
Приведем способ определения ассоциативности бинарной операции, используя тест ассоциативности по Лайту. Пусть дан конечный группоид 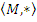 и фиксированный элемент
и фиксированный элемент 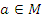 . Введем на
. Введем на 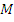 две новые бинарные операции
две новые бинарные операции 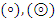 следующим образом:
следующим образом: 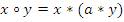 и
и 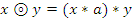 , получим группоиды
, получим группоиды 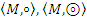 . Строим таблицы Кэли данных группоидов и сравниваем их соответствующие компоненты. Если
. Строим таблицы Кэли данных группоидов и сравниваем их соответствующие компоненты. Если 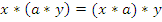 , то повторяем это для другого элемента и т. д. И если для любого
, то повторяем это для другого элемента и т. д. И если для любого 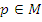 выполняется
выполняется 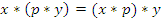 , то бинарная операция ассоциативна.
, то бинарная операция ассоциативна.
Прежде чем определять ассоциативность конечного группоида 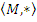 , желательно выяснить, имеет ли группоид минимальное порождающее множество. Если имеется порождающее множество
, желательно выяснить, имеет ли группоид минимальное порождающее множество. Если имеется порождающее множество 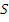 , отличное от множества
, отличное от множества 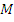 , то достаточно применить тест ассоциативности по Лайту к элементам множества
, то достаточно применить тест ассоциативности по Лайту к элементам множества 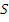 , так как все остальные элементы из
, так как все остальные элементы из 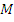 есть композиция элементов из
есть композиция элементов из 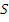 .
.
Рассмотрим пример:
Пусть дан группоид 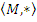 и
и 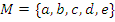 . Структура данного группоида определяется следующей таблицей Кэли:
. Структура данного группоида определяется следующей таблицей Кэли:
Таблица 2
|
* |
a |
b |
c |
d |
e |
|
a |
a |
a |
a |
d |
d |
|
b |
a |
b |
c |
d |
d |
|
c |
a |
c |
b |
d |
d |
|
d |
d |
d |
d |
a |
a |
|
e |
d |
e |
e |
a |
a |
Видно, что 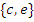 — порождающее множество группоида
— порождающее множество группоида 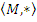 , так как
, так как 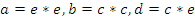
Проверим ассоциативность для элемента 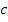 , используя тест ассоциативности по Лайту. Рассмотрим группоиды
, используя тест ассоциативности по Лайту. Рассмотрим группоиды 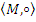 и
и 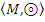 , причем
, причем 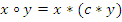 ,
, 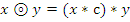 . Построим для них таблицы Кэли.
. Построим для них таблицы Кэли.
Строку 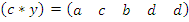 из таблицы 2 заносим в новую таблицу 3 в заглавную строку, и заполняем в соответствии с таблицей 2, причем заглавный столбец такой же как и в таблице 2. Затем заглавную строку
из таблицы 2 заносим в новую таблицу 3 в заглавную строку, и заполняем в соответствии с таблицей 2, причем заглавный столбец такой же как и в таблице 2. Затем заглавную строку 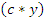 в таблице 3 меняем на строку
в таблице 3 меняем на строку 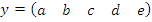 , а также меняем операцию
, а также меняем операцию 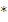 на
на 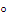 . В итоге получим таблицу Кэли для группоида
. В итоге получим таблицу Кэли для группоида 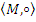 (таблица 4):
(таблица 4):
Таблица 3
|
|
a |
c |
b |
d |
d |
|
a |
a |
a |
a |
d |
d |
|
b |
a |
c |
b |
d |
d |
|
c |
a |
b |
c |
d |
d |
|
d |
d |
d |
d |
a |
a |
|
e |
d |
e |
e |
a |
a |
Таблица 4
|
|
a |
b |
c |
d |
e |
|
a |
a |
a |
a |
d |
d |
|
b |
a |
c |
b |
d |
d |
|
c |
a |
b |
c |
d |
d |
|
d |
d |
d |
d |
a |
a |
|
e |
d |
e |
e |
a |
a |
Столбец 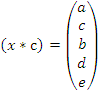 из таблицы 2 заносим в новую таблицу 5 в заглавный столбец, и заполняем в соответствии с таблицей 2, причем заглавная строка такая же как и в таблице 2. Затем заглавный столбец
из таблицы 2 заносим в новую таблицу 5 в заглавный столбец, и заполняем в соответствии с таблицей 2, причем заглавная строка такая же как и в таблице 2. Затем заглавный столбец 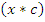 в таблице 5 меняем на столбец
в таблице 5 меняем на столбец 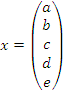 , а также меняем операцию
, а также меняем операцию 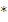 на
на 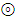 . В итоге получим таблицу Кэли для группоида
. В итоге получим таблицу Кэли для группоида 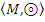 (таблица 6):
(таблица 6):
Таблица 5
|
|
a |
b |
c |
d |
e |
|
a |
a |
a |
a |
d |
d |
|
c |
a |
c |
b |
d |
d |
|
b |
a |
b |
c |
d |
d |
|
d |
d |
d |
d |
a |
a |
|
e |
d |
e |
e |
a |
a |
Таблица 6
|
|
a |
b |
c |
d |
e |
|
a |
a |
a |
a |
d |
d |
|
b |
a |
c |
b |
d |
d |
|
c |
a |
b |
c |
d |
d |
|
d |
d |
d |
d |
a |
a |
|
e |
d |
e |
e |
a |
a |
Сравнивая таблицы 4 и 6, видно, что их соответствующие компоненты совпадают, то есть 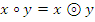 . Это и означает, что
. Это и означает, что 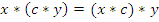 , то есть операция ассоциативна относительно элемента
, то есть операция ассоциативна относительно элемента 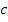 .
.
Аналогично можно показать, что 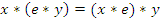 .
.
Таким образом, группоид 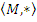 есть полугруппа. И для нее, в силу теоремы, выполняется также обобщенный закон ассоциативности.
есть полугруппа. И для нее, в силу теоремы, выполняется также обобщенный закон ассоциативности.
Можно, однако, при установлении ассоциативности группоида при помощи теста ассоциативности по Лайту, использовать немного упрощенный вариант, который уже не предполагает построение группоидов 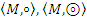 [3]. Вернемся к рассмотренному ранее примеру. В таблице 3 вместо заглавного столбца
[3]. Вернемся к рассмотренному ранее примеру. В таблице 3 вместо заглавного столбца 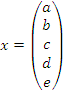 запишем столбец
запишем столбец 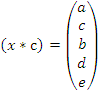 из таблицы 2. Получим таблицу 7:
из таблицы 2. Получим таблицу 7:
Таблица 7
|
|
a |
c |
b |
d |
d |
|
a |
a |
a |
a |
d |
d |
|
c |
a |
c |
b |
d |
d |
|
b |
a |
b |
c |
d |
d |
|
d |
d |
d |
d |
a |
a |
|
e |
d |
e |
e |
a |
a |
И проверяем, совпадают ли строки таблицы 7 со строками таблицы 2 (совпадение столбцов следует из построения таблицы 3), то есть проверяем совпадение, например, строки 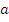 в таблице 7 со строкой
в таблице 7 со строкой 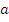 в таблице 2 и т. д. Если все строки совпадают, то группоид ассоциативен относительно элемента
в таблице 2 и т. д. Если все строки совпадают, то группоид ассоциативен относительно элемента 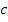 . Аналогичное проделывает для элемента
. Аналогичное проделывает для элемента 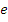 .
.
Таким образом, для проверки ассоциативности бинарной операции любого конечного группоида достаточно построить таблицу, аналогичную таблице 7, и сравнить соответствующие строки полученной таблицы и исходной таблицы Кэли группоида. Тест ассоциативности по Лайту позволяет просто и быстро (в отличие от обычного перебора всех возможных вариантов) проверить ассоциативность бинарной операции данного конечного группоида с заданной таблицей Кэли. Нетрудно заметить, что этот тест применим для квазигруппы и лупы, так как эти алгебры есть частный случай группоида.
Литература:
1. Белоусов В. Д. Основы теории квазигрупп и луп — М.: Наука, 1967. — 225 с.
2. Глухов М. М. Елизаров В. П. Нечаев А. А. Алгебра Учебник в 2-х т. Т1 — М.: Гелиос АРВ, 2003–336 с.
3. Клиффорд А. Престон Г. Алгебраическая теория полугрупп том 1. Пер. с англ. — М.: Мир, 1972. — 286 с.
4. Куликов Л. Я. Алгебра и теория чисел: Учебное пособие для педагогических институтов — М.: Высшая школа, 1979. — 559 с.
5. Cayley, Arthur. «On the theory of groups, as depending on the symbolic equation 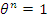 ", Philosophical Magazine, Vol. 7 (1854), pp. 40–47.
", Philosophical Magazine, Vol. 7 (1854), pp. 40–47.