Каждый инновационный процесс, независимо от сферы деятельности, непосредственно связан с финансированием, то есть с привлечением инвестиционных средств. Безусловно, каждый инвестор заинтересован в перспективности абсолютного использования имеющихся финансовых ресурсов с максимальной доходностью и минимальными рисками. Потенциальный инвестор оценивает хозяйственную систему, с которой желает взаимодействовать, по следующим направлениям [5, с. 31]:
– исследование элементов входящих в систему;
– определение существующего положения по наличию всех необходимых ресурсов;
– наличие рисков;
– устойчивость развития хозяйственной системы;
– мониторинг развития и экономические показатели;
– инфраструктура хозяйственной системы;
– коммуникационное развитие.
Моделирование процесса планирования сбалансированного развития инновационной и инвестиционной деятельности хозяйственных систем предполагает оценку состояния, прогнозирование, планирование. Применение моделирования как процесса планирования сбалансированного развития инновационной и инвестиционной деятельности хозяйственных систем связано с отсутствием полной и достоверной информации о деятельности и с невозможностью оценки имеющейся в распоряжении руководителя информации, прежде всего из-за ее огромного объема.
Необходимыми и взаимосвязанными условиями инновационной деятельности хозяйственных систем макро-, мезо- и микроуровней являются наличие капитала у потенциального инвестора, а также его желание разместить свой капитал на поставленных условиях в конкретных секторах экономики. Наличие прибыльных, динамично развивающихся секторов экономики, способствует эффективному размещению и передвижению капитала в прямом и обратном направлениях [10, с. 85].
Инвесторы, инвестиционные посредники, хозяйственные системы микроуровней, государство и его отдельные регионы выступают сторонами, обеспечивающими этапы инвестиционной деятельности. Все вышеперечисленные стороны осуществляют свою деятельность на различных этапах инвестиционного процесса, преследуют собственные цели и показывают личные интересы, что характеризует многомерность инвестиционно-инновационной деятельности [7, с. 57].
Согласование и координация интересов инвесторов и хозяйственных систем, позволяет избежать всевозможных противоречий. Хозяйственные системы в макро-, мезо- и микроуровней выступают субъектом интереса в моделировании. Отличные интересы имеет инвестор, его интересы не всегда совпадают с мотивациями хозяйственных систем. Интересы между инвесторами и хозяйственными системами принимают различные значения, в зависимости от уровня хозяйствования (макро-, мезо- и микро-).
Модели, применяемые для плановых расчетов, используются на разнообразных этапах планирования. Наиболее часто они применяются для прогноза развития производственных сил страны. При построении моделей для нашего диссертационного исследования необходимо исходить из соответствия оптимального решения реализация, которых предоставит требуемый вариант планирования сбалансированности. Моделирование данных процессов необходимо строить по блокам, для чего формируется система моделей [6, с. 58].
При постановке задач в системе моделей применяются разные типы согласования: вертикальный - при постановке задач (задачи развития макро-, мезо-, микроуровней); горизонтальный – для задач одного уровня и смешанного (каждый уровень рассматривается отдельно либо макро- и мезо-; макро- и микро-; мезо- и микроуровень) [8, с. 115].
В источниках рассматриваются, различные по сложности модели, а мы же придерживаемся наиболее простой (рисунок 1).
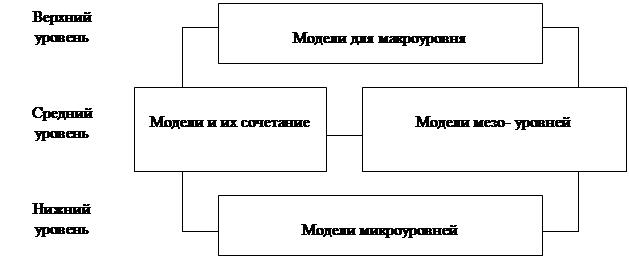
Рис. 1 Модели макро-, мезо-, микроуровней и их сочетание
Сибирская Е.В. считает, что процесс согласования призван обеспечить содержательную корректировку параметров, уменьшающую расхождение между экзо- и эндогенными одноименными параметрами отдельных блоков: например, между агрегированным выпуском продукции и суммой выпусков по составляющим продуктам в детализированной классификации, рассчитанным по разным задачам; между значениями объемов потребления ресурсов отраслями, определяемыми по решениям изолированных задач с общим наличием ресурса, и т.д. Конечной целью согласования является получение приближенного решения исходной задачи в детализированной номенклатуре при наибольшем значении конечного показателя целевой функции. В качестве последнего обычно берется фонд конечного потребления в целом по стране [3, с. 124].
Основные прикладные результаты работ по системам моделей относятся в основном к реализации только отдельных блоков системы. Согласование же решений между отдельными блоками все еще остается наиболее трудной проблемой для практической реализации. Это связано с тем, что, во-первых, процессы согласования решений задач разных уровней формируются по нестрогим в математическом отношении алгоритмам и потому сложны и трудоемки. Они больше похожи на эвристические, особенности их зависят от вида реализуемой задачи и ее свойств [11, с. 20].
В связи с этим при работе с прикладными схемами решения задач чаще используют термин «увязка решений», подчеркивая этим не строгость применяемых вычислительных схем в сравнении со строгими, где используются термины «согласование». Во-вторых, изменяется и расширяется класс реализуемых задач. Это приводит к изменениям как в самих моделях, так и в схемах их взаимодействия. В частности, решение народнохозяйственных и районных задач на основе укрупненной информации межотраслевых балансов при одинаковой затратной и временной структуре исходных данных (без выделения условий действующих и вновь вводимых мощностей, без привлечения информации отраслевых проектов и т. п.) приводило к простым схемам обмена информацией. Привлечение же в настоящее время на локальном уровне детализированной информации отраслевых и территориальных задач, более адекватно отражающих действительность, требует существенного изменения принципов взаимосвязи [4, с. 243]..
Существо излагаемого ниже подхода состоит во «вписании» («встраивании») информации локальной задачи сбалансированного развития инновационной и инвестиционной деятельности хозяйственных систем (средний уровень) в задачу развития страны (верхний уровень) в форме технологического способа (вектора с компонентами затрат). В данном технологическом способе (или нескольких способах) в разрезе действующей продуктовой номенклатуры инновационной деятельности задачи верхнего уровня отражаются как затраты, так и выпуск нескольких видов инновационной продукции. Информация для этих способов получается агрегированием информации по результатам решения локальных задач.
Предполагается, что для задач обоих уровней информация строится в стоимостном виде в одной системе цен, и выдерживается принцип разделения целевых установок для задач разных уровней: на верхнем осуществляется укрупненная оценка народнохозяйственной эффективности и сбалансированности прогноза развития инновационной и инвестиционной деятельности хозяйственных систем, на локальном - построение детализированного прогноза развития при выделенных инвесторами ресурсах. На локальном уровне осуществляется корректировка информации для задачи верхнего уровня с учетом изменившихся конкретных условий хозяйственных систем.
Рассмотрим только схему увязки решений задач развития хозяйственных систем с соответствующими условиями межрегиональной межотраслевой задачи. В качестве примера возьмем модели, в которых представлен временной разрез создаваемых производственных мощностей по годам ввода [2, с. 84] - для задачи верхнего уровня и многопериодный вариант мезо- модели [1, с. 46] - для задачи среднего уровня. Выбор типа моделей, позволяющих выделять приросты производства в форме вариантов ввода новых предприятий или расширения действующих, определен тем, что они более приспособлены для оценки новых технологий, представляемых в форме как действующих и вновь вводимых предприятий, так и соответствующих направлений капитальных вложений.
В расчетах на народнохозяйственном уровне в ИЭиОПП используются обычно две модели: межотраслевая межрегиональная модель в полудинамической постановке и межрегиональная модель в полностью динамической постановке. С их помощью рассчитываются варианты развития производительных сил в временном разрезах с укрупненными показателями межотраслевых и территориальных пропорций. Первая строится на последний год планового периода, по ней рассчитываются стратегические направления развития производительных сил с указанием экономических показателей последнего года планового периода. Уточнение динамики по временным отрезкам между базовым и последним годом периода осуществляется с помощью динамической модели. Из полудинамической в динамическую модель поступает информация об области («конусе») возможной вариации уровней производства в периоде, в частности о минимально необходимом уровне роста продукции в последнем году периода, объеме основных фондов на конец периода. Обратный поток составляет нормативная информация по материальным и трудовым затратам для условий последнего года и нормативам капиталовложений в целом за период [4, с. 98].
В нашем случае многопериодный вариант модели хозяйственной системы непосредственно взаимодействует с народнохозяйственной задачей в динамической постановке как с задачей адекватной структуры (по крайней мере, в отношении представления динамики). Как известно, межрегиональные межотраслевые модели предназначены для расчетов показателей территориальных пропорций. Основное внимание уделяется обоснованию прогнозов развития отраслей общесоюзной специализации. Информация по этим отраслям представлена в межрегиональной модели в более детализированном виде, чем по отраслям районной специализации, а также локальным ресурсам [9, с. 84].
Модели предназначены для расчетов детализированных показателей по элементам хозяйства в пределах исследуемой территории. Здесь уже более детально представлены отрасли внутрирайонной специализации, условия по охране среды, балансы продукции ограниченной транспортабельности; конкретизируются пункты размещения новых предприятий; достигается адресность показателей развития конкретных предприятий, что составляет основу для разработки ряда предплановых и проектных документов.
Динамическая межрегиональная модель включает следующие условия и ограничения:
1) балансы производства и распределения продукции
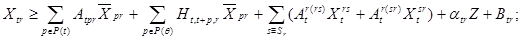(1)
2) балансы трудовых ресурсов
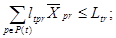(2)
3) баланс, основных фондов на конец периода
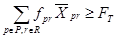; (3)
4) ограничения на выпуск продукции на отдельных мощностях
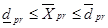(для некоторых p,r); (4)
5) неотрицательность переменных
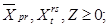(5)
6) целевая функция
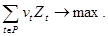(6)
Модель определена на период в T лет и приведена в упрощенном виде. При записи модели использовались следующие условные обозначения.
Индексы:
t, p – годы планового периода (p = 0 соответствует доплановому периоду);
P (t) – множество индексов лет,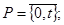 
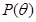- множество индексов лет, определяемых сроками строительства объектов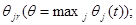 
r,s,m – индексы районов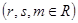 
;
R и Sr – соответственно множество всех индексов районов и районов, смежных с районом r;
i,j – продукты (отрасли);
I – множество продуктов (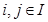
); для отраслей транспорта I принимает номер 
;
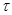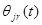- период строительства объектов в j-й отрасли в r-м районе в году t.
Неизвестные для района r:
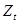- объем непроизводственного потребления в целом по стране за год t;
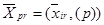- объем выпуска i-й продукции с мощностей, введенных в году p;
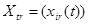- выпуск продукции i-го вида в году t на мощностях действующих в году t; 
;
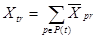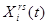- объем поставок i-й продукции в году из района r в район s.
Параметры для района r года t:
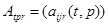- затраты продукции i-го вида на единицу производства продукции j-й отрасли в году t на мощностях, введенных в году p, а также капитальные вложения в действующие мощности;
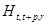- затраты капитальных вложений i-го вида, осуществляемые в t-м году по j-й отрасли на мощностях, вводимых в (t+p)-м году;
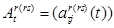- коэффициенты затрат транспорта и направлений межрегиональных поставок: для строк отрасли транспорт 
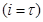они отрицательные и обозначают транспортные затраты организации r-го региона на доставку продукции вида j из r-го района в s-й; для строк транспортабельной продукции 
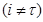они равны (-1) для района вывоза и (+1) – для района ввоза, остальные коэффициенты нулевые;
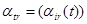- доля в общем фонде непроизводственного потребления страны фонда t-го года, приходящаяся на i-ю продукцию;
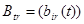- фиксированная часть конечного пользования продукции i-го вида (капитальных вложений в мощности, вводимые за пределами рассматриваемого периода, продукция оборотного значения, сальдо экспорта и импорта для пограничных районов и др.);
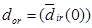- мощность по выпуску i-й продукции на начало планового периода;
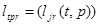- затраты в t-м году на производство единицы j-й продукции на мощностях, введенных в году p; vt – коэффициент предпочтения благ конечного использования года t перед соответствующими благами последующих лет.
Задача модели хозяйственной систем формулируется следующим образом: определить вариант размещения и формирования объектов отраслей специализации системы, комплексирующих производств и элементов производственной инфраструктуры межрайонного и общерайонного значения при условии минимизации суммарных приведенных затрат на выполнение заданной репрограммы с учетом достижения намечаемого на перспективу уровня жизни населения. Приводимая ниже модель представлена в чрезвычайно сжатом виде, максимально приближенном к форме записи динамической межрегиональной модели народнохозяйственного уровня.
Она включает:
1) балансы производства и распределения продукции
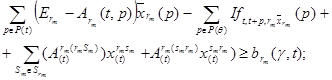(7)
2) балансы локальных ресурсов
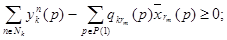(8)
3) ограничения на возможный масштаб использования ресурсов
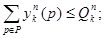(9)
4) неотрицательность переменных
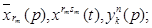(10)
5) целевая функция
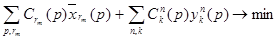(11)
При записи модели хозяйственной системы использованы обозначения межрегиональной модели, их содержательные трактовки аналогичны межрегиональной модели. В качестве дополнительных взяты:
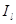- множество индексов j;
il, jl – индексы продукции, входящие в отрасль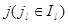 
;
rm – индексы m локальной территории, входящих в район r;
R(r) – множество индексов подрайонов r-го района. (В целях упрощения изложения самого метода встраивания под районом будем понимать хозяйственную систему в задаче народнохозяйственного уровня);
K – множество индексов ресурсов,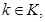 
k – индекс вида локальных ресурсов;
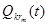- наличие k-го ресурса в подрайоне rm;
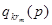- расход k-го вида ресурса на единицу выпуска продукции ji;
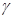- номер шага процесса решения данных задач (параметры с индексом 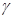изменяются по интеграции процесса обмена информацией между двумя задачами, в целях упрощения записи индекс 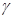при переменных опущен);
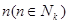- индекс категории ресурса вида k;
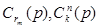- дисконтированные затраты на функционирование
соответствующих элементов хозяйства.
Таким образом, рассматриваемая схема увязки решений задач является лишь отдельным элементом системы моделей. Схема, например, не охватывает связей с задачами других районов и отраслевых комплексов. Внешние связи исследуемой экономической системы с другими территориальными единицами и отраслями считаются фиксированными. Другой посылкой является формирование на основе решения задачи уровня II лишь одного способа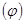 
. Он «представляется» как дополнительный к условиям блока межрегиональной модели, который отражает соответствующий район.
Литература:
1. Бандман, М.К. Территориально-производственные комплексы: теория и практика предплановых исследований [Текст] / М.Б. Бандман. – Новосибирск: Наука Сиб. отделение, 1980.
2. Гранберг, А.Г. Оптимизация территориальных пропорций народного хозяйства [Текст] / А.Г. Гранберг. – М.: Экономика, 1973; Мелентьев, Б.В. Экспериментальные расчеты по оптимизационной динамической региональной модели [Текст] // Исследование межотраслевых территориальных пропорций. Новосибирск: Наука. Сиб. отделение, 1980. – С. 71-92
3. Сибирская, Е.В. Стратегия развития региональных промышленно-производственных комплексов на основе интеграции экономических процессов [Текст]: монография / Е.В. Сибирская. – Орел: Издательство ОГТУ, 2004.
4. Сибирская, Е.В. Стратегия развития региональных промышленно-производственных комплексов на основе интеграции экономических процессов [Текст] : дис… доктора экономических наук: 080005 / Е.В. Сибирская; [Место защиты: Воронеж. гос. техн. ун-т]. – Воронеж, 2004. – 435 с.
5. Серебрякова Н.А., Пахомова Т.А. Мониторинг инновационной и инвестиционной деятельности хозяйственных систем [Текст] / Н.А. Серебрякова, Т.А. Пахомова // Теоретические и прикладные вопросы экономики сферы услуг. 2014. № 2. С. 27-42.
6. Серебрякова Н.А., Грищенко Н.В. Прогнозирование экономических показателей на основе трендовых моделей [Текст] / Н.А.Серебрякова, Н.В. Грищенко // ФЭС: Финансы, Экономика. Стратегия. 2012. № 3. С. 55-59.
7. Серебрякова Н.А., Смольянова Е.Л. Основные проблемы развития инновационно-инвестиционного потенциала Воронежской области [Текст] / Н.А.Серебрякова, Е.Л. Смольянова // Региональная экономика: теория и практика. 2009. № 2. С. 52-60.
8. Серебрякова Н.А. Основные проблемы планирования инновационного развития хозяйственных систем [Текст] / Н.А.Серебрякова // Экономика. Инновации. Управление качеством. 2014. № 4 (9). С. 115-116.
9. Серебрякова Н.А. Теоретические аспекты планирования сбалансированного развития инновационно-инвестиционной деятельности предприятия [Текст] / Н.А.Серебрякова // Экономика. Инновации. Управление качеством. 2014. № 4 (9). С. 83-84.
10. Серебрякова Н.А. Государственное регулирование развития региональной инновационной системы [Текст] / Н.А.Серебрякова // Экономика. Инновации. Управление качеством. 2014. № 4 (9). С. 85.
11. Серебрякова Н.А. Перспективные направления развития инновационной активности предприятий пищевой промышленности [Текст] / Н.А. Серебрякова // Теоретические и прикладные вопросы экономики сферы услуг. 2014. № 8. С. 19-22.
