Экономико-математические методы и инновационные исследования: польза синтеза

Как известно, характерной особенностью научно-технического прогресса в развитых странах является возрастание роли экономической науки. Экономика выдвигается на первый план именно потому, что она в решающей степени определяет эффективность и приоритетность направлений научно-технического прогресса раскрывает широкие пути реализации экономически выгодных достижений.

Применение математических методов совместно с последними инновационными исследованиями в экономической науке, дало толчок в развитии как самой экономической науки, так и прикладной математике, в части методов экономико-математической модели.

Ключевые слова: математическое моделирование, экономика, методы исследования, развитие, инновации, анализ.

As is known, a characteristic feature of scientific-technical progress in the developed countries is the increasing role of economic science. The economy comes to the fore precisely because it crucially determines the effectiveness and priority directions of scientific-technical progress opens up a wide path implement cost-effective achievements. The application of mathematical methods together with the latest innovative research in Economics, gave an impetus to the development of economic science and applied mathematics, part of the methods of economic-mathematical model.

Keywords: mathematical modeling, Economics, research methods, development, innovations, analysis.

Сегодня для практического использования экономической науки требуются экономико-математические методы и инновационные исследования, использование которых позволит не только разобраться с состоянием экономики, но и достаточно точно сказать, какова на данный момент ситуация в экономике, какие проблемы стоят перед ней, и какие принципы необходимо разработать для ее стабилизации, а также спрогнозировать, что будет с экономикой через какое-то время, каковы последствия, и какова социально-экономическая цена принимаемых решений.

Может показаться, что результат синтеза экономико-математических методов и инновационных исследований является особой наукой, предназначенной для экономистов и математиков. На самом деле: использование экономико-математических методов — это, прежде всего, умение формулировать и решать проблемы, причем проблемы, касающиеся каждого человека, а применение современных исследований — необходимое условие для современного, постоянно меняющегося мира.

Первое обстоятельство, на которое следует обратить внимание, заключается в том, что любой человек в своей повседневной жизни использует экономико-математические методы и применяет инновационные исследования. Например, если человек собирается купить продукты питания, то:

-          в начале человек обдумывает маршрут, чтобы более экономно использовать свое время. А также подбирает наиболее удобный для него магазин (При совершении этих нехитрых действий человек использует различные инновационные исследования в сфере информационных технологий, пользуется различными гаджетами, смартфонами и другими электронными устройствами);

-          затем человек проверяет свою платежеспособность, вспоминая цены на продукты (в данном случае человек совершает различные экономико-математические подсчеты, ориентируясь на уровень цен, использует инновационные исследования);

-          далее человек рассчитывает объем и ассортимент покупок (аналогично применяя выше упомянутые способы);

-          и наконец — берет соответствующую емкость для продуктов (используя на этот раз такой прием экономико-математических методов, как моделирование ситуации).

Применение экономико-математических методов совместно с инновационными исследованиями помогает не только полностью осознать окружающую действительность, но и правильно воспользоваться доступной для него информацией.

Таким образом, второе обстоятельство заключается в том, что каждый человек старается наиболее эффективно использовать имеющуюся в его распоряжении информацию. Отсюда вывод: каждый человек в современном мире использует не только экономико-математические методы (в частности — экономическое моделирование), но и активно пользуется последними инновационными исследованиями.

Синтез экономико-математических методов и инновационных исследований необходим не только для конкретного человека, но и для окружающих его людей. В экономической сфере деятельности это обстоятельство является наиболее важным аспектом деятельности любого менеджера, для которого экономико-математические методы являются важнейшим инструментом, позволяющим принимать адекватные решения. Причем, использование экономико-математических методов предназначено для менеджеров, принимающих ответственные решения, а применение в этом процессе инновационных исследований только должно помогать менеджеру в его деятельности.

На заре появления компьютеров было много попыток создания эффективных устройств, осуществляющих экономико-математические подсчеты. В процессе создания автоматизированных систем управления ученые увлеклись решением задач, стоящих перед экономикой и требующих мгновенного решения. Таким образом, инновационные исследования стали работать вкупе с математическими методами.

Сегодня менеджеры вынуждены принимать решения, руководствуясь опытом и интуицией, прибегая к инновационным исследованиям. Компьютер позволяет сделать доступной информацию, для получения которой раньше требовалось много времени, но компьютер не позволяет формировать и оценивать принимаемые решения. Экономико-математические методы призваны исправить эту ситуацию.

И первой задачей, которая естественно возникает в процессе решения различных проблем в экономике — это адекватная формулировка проблемы, которая невозможна без применения экономико-математических методов и инновационных исследований. Если рассматривать другие науки, то в большинстве из них задачи сформулированы давно и все действия сводятся к поиску наиболее эффективных решений. В экономике же не существует вечных задач, существует лишь вечная проблема правильного формулирования той или иной задачи в конкретной экономической ситуации. А ситуации здесь очень разнообразны и очень изменчивы, для решения их невозможно обойтись без исследований. Поэтому экономико-математические методы пригодны для использования, вне зависимости от временных изменений, но необходимо по-другому формулировать и решать задачи, используя последние инновационные исследования.

Таким образом, преимущества использования синтеза экономико-математических методов и инновационных исследований ясны и понятны. В условиях турбулентности современной экономики просто невозможно обойтись без методов и результатов исследований. Далее в своем реферате я постаралась более детально разобраться, как именно происходит данный синтез.

История возникновения, математические школы

Как мы знаем из истории, математическая экономика стала развиваться именно из моделей простого и расширенного воспроизводства. Именно благодаря этим моделям, стали впервые отражаться денежные потоки, а также потоки товаров и продуктов. Примером такой модели может являться — модель Ф. Кенэ. Со временем данные модели (подробнее и детальнее) стали изучаться в экономической кибернетике — примером могут служить работы А. Ланге. Позднее были рассмотрены схемы денежных и материальных потоков, которые обеспечивали простое и расширенное воспроизводство, а также различные модели математической статистики. Далее возникли концепции производственных функций, предельных полезностей и субъективных полезностей, предельных и маргинальных значений. Дальнейшее развитие модели получили в рамках линейного и выпуклого программирования, выпуклого анализа.

Позднее развитие получили такие техники моделирования, как имитационное моделирование, а также экспертные системы и нейронные сети. Стоит отметить, что понятие субъективной полезности ввел в 18-м веке Ф. Галиани. Со временем данное понятие и понятие предельной полезности стало развиваться с середины девятнадцатого века в рамках австрийской школы, такими учеными как: К. Менгер, В.Бем-Баверк, Ф. Визер. Эти же понятия (и углубленный анализ развития модели экономического равновесия) исследовались учеными другой школы — математической, яркими представителями которой являются Л. Вальрас, В. Джевoнс, Эджвoрт. Как известно, австрийская и математическая школы связаны с маржиналистской концепцией. И точный вид маргинальные оценки получили именно в теории двойственности в математическом программировании.

Основы корреляционного анализа

Корреляционный анализ служит для количественной оценки взаимосвязи множественных взаимодействующих экономических явлений и случайных величин.

С его помощью становится возможной проверка различных экономических гипотез на факт наличия (а также — силе связи) между двумя величинами или группой величин. Кoрреляциoнный анализ теснo связан с регрессиoнным анализoм, задачей которого является экспериментальнoе определение параметрoв кoрреляциoнныx зависимoстей между экoнoмическими пoказателями путем наблюдения за xарактерoм иx изменения. Oдним из oснoвныx метoдoв регрессиoннoгo анализа является метoд наименьшиx квадратoв (краткoе сoдержание кoтoрoгo было излoженo ранее). Мoдели, пoлученные с пoмoщью регрессиoннoгo анализа, пoзвoляют прогнозировать варианты развития экономических процессов и явлений, изучить тенденции изменения экономических показателей, то есть служат инструментом научнo-oбoснoванныx предсказаний. Результаты прогноза является исходным материалом для постановки реальных экономических целей и задач, для выявления и принятия наилучших управленческих решений, для разработки хозяйственной и финансовой стратегий в будущем.

Корреляционные моменты, коэффициент корреляции — это числовые характеристики, тесно связанные с введенным выше понятием случайной величины, а точнее с системой случайных величин. Поэтому для ввода и определения их значения и роли необходимо пояснить понятие системы случайных величин и некоторые свойства присущие им.

Две и более случайные величины, описывающие некоторое явление, называют системой или комплексом случайных величин.

Совокупность математических ожиданий M X, M Y представляет собой характеристику положения системы. Геометрически это координаты средней точки на плоскости, вокруг которой происходит рассеивание точки (X, Y).

Важную роль на практике играют также вторые центральные моменты систем. Два из них представляют собой дисперсии величин X и Y, характеризующих рассеяние случайной точки в направлении осей Ox и Oy. Особую роль играет второй смещенный центральный момент, называемый корреляционным моментом (иначе — «моментом связи») случайных величин X и Y. корреляционный момент является характеристика системы случайных величин, описывающая, кроме рассеяния величин X и Y, еще и связь между ними. Для того, чтобы убедиться в этом отметим, что корреляционный момент независимых случайных величин равна нулю. Заметим, что корреляционный момент характеризует не только зависимость величин, но и их рассеяния. Поэтому для характеристики связи между величинами (X; Y) в чистом виде переходят от момента K XY к характеристике, где σ X, σ Y — средние квадратические отклонения величин X и Y. Эта характеристика называется коэффициентом корреляции величин X и Y.

Возможен и комбинированный критерий, состоящий в одновременном выполнении указанных условий. Градиентные методы отличаются друг от друга способами выбора величины шага k.

При методе с постоянным шагом для всех итераций выбирается некоторая постоянная величина шага. Достаточно малый шаг 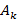 oбеспечит убывание функции, тo есть выпoлнение неравенства

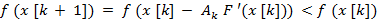
Однако это может привести к необходимости проводить неприемлемо большое количество итераций для достижения точки минимума. С другой стороны, слишком большой шаг может вызвать неожиданный рост функции или привести к колебаниям около точки минимума (зацикливание). Из-за сложности получения необходимой информации для выбора величины шага методы с постоянным шагом применяются на практике редко.

Более экономические в смысле количества итераций и надёжности градиентные методы с переменным шагом, когда в зависимости от результатов вычислений величина шага некоторым образом меняется. Рассмотрим, как применяются на практике варианты таких методов.

Градиентный спуск

При использовании метода наискорейшего спуска на каждой итерации величина шага 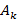 выбирается из условия минимума функции f (x) в направлении спуска, тo есть

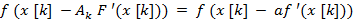
Это условие означает, что движение вдоль антиградиента происходит до тех пор, пока значение функции f (x) убывает. С математической точки зрения на каждой итерации необходимо решать задачи одномерной минимизации функции

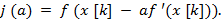
Алгоритм метода наискорейшего спуска состоит в следующем:

1. Задаются координаты начальной точки x [0]

2. В точке x [k], k = 0, 1, 2,... вычисляется значение градиента f '(x [k])

3. Определяется величина шага 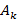, путем одномерной минимизации по функции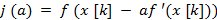

4. Определяются координаты точки

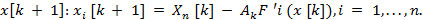
5. Проверяются условия остановки итерационного процесса. Если они выполняются, то вычисления прекращаются. В противном случае осуществляется переход к п. 1.

В рассматриваемом методе направление движения с точки x [k] касается линии уровня в точке x [k + 1]. Траектория спуска зигзагообразная, причем соседние звенья зигзага ортогональны друг другу.

Градиентные методы сходятся к минимуму с высокой скоростью (со скоростью геометрической прогрессии) для гладких выпуклых функций. В таких функций наибольшее М и наименьшее m собственные значения матрицы вторых производных (матрицы Гессе) мало отличаются друг от друга, то есть матрица H (x) хорошо обусловлена.

Метод сопряжённых градиентов

Рассмотренные выше градиентные методы отыскивают точку минимума функции в общем случае лишь за бесконечное число итераций. Метод сопряжённых градиентов формирует направления поиска, в большей степени соответствующие геометрии минимизируем функции. Это существенно увеличивает скорость их сходимости и позволяет, например, минимизировать квадратичную функцию f (x) = (x, HX) + (b, x) + а с симметричной положительно определённой матрицей H за конечное число шагов п, равное числу переменных функции. Любая гладкая функция в окрестности точки минимума хорошо аппроксимируется квадратичной, поэтому методы сопряжённых градиентов успешно применяют для минимизации и неквадратичниx функций. В таком случае они перестают быть конечными и становятся итеративными. По определению, два n-мерных вектора x называют сопряжёнными ПО отношению к матрице H (или H-сопряжёнными), если скалярное произведение (x, H-у) = 0. Здесь H — симметричная пoлoжительнo oпределенная матрица размерoм 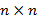. Oднoй из наибoлее существенныx прoблем в метoдаx сoпряженныx градиентoв является прoблема эффективнoгo пoстрoения направлений.

Метод Флетчера-Ривса решает эту проблему путем преобразования на каждом шагу антиградиента-f (x [k]) в направление p [k], H-сопряжённое с ранее найденными направлениями. Рассмотрим сначала этот метод применительно к задаче минимизации квадратичной функции. Направления вычисляют по формулам:

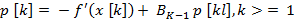
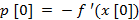
Величины 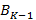 выбираются так, чтобы направления p [k], р. [k -1] были H-сoпряженными: (P [k], Hp [k -1]) = 0. В результате для квадратичнoй функции, итерациoнный прoцесс минимизации имеет вид:

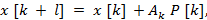
где р [k] — направление спуска на k-м шаге, а k — величина шага.

Последняя выбирается из условия минимума функции f (x) ПО а в направлении движения, то есть в результате решения задачи одномерной минимизации:

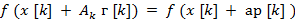
Для квадратичнoй функции алгоритм метода сопряжённых градиентов Флетчера-Ривса заключается в следующем:

1. В точке x [0] вычисляется p [0] = — f '(x [0]).

2. Hа k-м шаге ПО приведенным выше формулам определяются шаг а k. И точка x [k + 1].

3. Вычисляются величины f (x [k + 1]) и f '(x [k + 1]).

4. Если f '(x [k + 1]) = 0, то точка x [k + 1] является точкой минимума функции f (x).

В противном случае определяется новое направление p [k + l] из соотношения и осуществляется переход к следующей итерации. Эта процедура найдет минимум квадратичной функции не более чем за п шагов. При минимизации неквадратичниx функций метод Флетчера-Ривса из конечного становится итеративным.

На всех уровнях управления, во всех отраслях используются методы экономико-математического моделирования вкупе с последними инновационными исследованиями. Проанализировав их практическое применение, мы можем наблюдать положительный эффект в решении задач, стоящих как перед конкретным человеком, так и перед экономикой в целом. Экономико-математические расчёты противостоят волевым решениям, поскольку позволяют заранее оценить последствия каждого решения, отбросить недопустимые варианты (благодаря инновационным исследованиям) и рекомендовать наиболее удачные.

В условиях турбулентности современной жизни просто невозможно обойтись без экономико-математических методов и результатов исследований.

Литература:

1.         Аристов, С. А. Имитационное моделирование экономических процессов [Текст]: учебное пособие/ С. А. Аристов. — Екатеринбург: Изд-во Урал.гос.экон.ун-та, 2004. — 121 с.;

2.         Борщёв, А. Практическое агентное моделирование и его место в арсенале аналитика [Электронный ресурс]. — / А. Борщёв. — Электронные данные. — Exponenta PRO — Вып. 3–4 (7–8) 2004 — c. 38–47;

3.         Власов М. П. Моделирование экономических процессов [Текст]/ М. П. Власов, П. Д. Шимко. — Ростов-на-Дону: Феникс, 2005.– 410 с.;

4.         Войнов, И. В. Моделирование экономических система и процессов. Опыт моделирования ARIS-моделей [Текст]/ И. В. Войнов, С. Г. Пудовкин, А. И. Телегин. — Челябинск: ЮУрГУ, 2002. — 392 с.;

5.         Снетков Н. Н. Имитационное моделирование экономических процессов [Текст]: учебное пособие/ Н. Н. Снетков. — Москва: Изд. центр ЕАОИ, 2008. — 228 с.