Задача автоматического управления технологическими процессами предполагает широкое использование ЭВМ с целью обработки текущей измерительной информации о состоянии конкретного процесса и выработки оптимальных оперативных управляющих воздействий по этой информации. Поэтому важной составной частью задачи управления является идентификация процессов по принятой модели и наблюдаемой информации. В статье на примере линейной модели управления нагревом массивного тела (I) рассматривается задача восстановления распределения температуры по телу на основе измерения ее в отдельных точках поверхности тела. Применением принципа дуальности задач управления и наблюдения вопрос сводится к решению задач об условном экстремуме.
1. Задача об определении распределения температуры в нагреваемом «стержне» по наблюдению изменения температуры в отдельной его точке.
Рассмотрим нагрев бесконечной однородной пластины конечной толщины 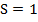 в предположении, что начальная температура пластины и процесс нагрева проходят идентично по толщине. Тогда достаточно анализировать ход процесса в некотором «стержне», распложенном в пластине ортогонально ее боковой поверхности (1). Пусть распределение температуры по толщине пластины
в предположении, что начальная температура пластины и процесс нагрева проходят идентично по толщине. Тогда достаточно анализировать ход процесса в некотором «стержне», распложенном в пластине ортогонально ее боковой поверхности (1). Пусть распределение температуры по толщине пластины 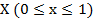 и во времени
и во времени 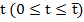 описывается функцией
описывается функцией 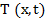 определяемой в прямоугольнике
определяемой в прямоугольнике 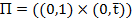 , где
, где 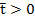 — фиксированное число. Внутри отрезка
— фиксированное число. Внутри отрезка 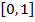 и при
и при 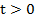 распределение температуры
распределение температуры 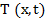 подчиняется уравнению теплопроводности.
подчиняется уравнению теплопроводности.
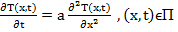 (1)
(1)
Здесь 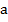 - коэффитциент температуропроводности. На концах «стержня» приняты следующие условия теплопередачи:
- коэффитциент температуропроводности. На концах «стержня» приняты следующие условия теплопередачи:
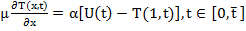
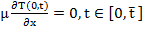 (2)
(2)
где 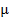 - коэффициент теплопроводности,
- коэффициент теплопроводности, 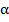 — коэффициент теплообмена между греющей средой, соответственно с одной стороны, плитой, левый конец пластины
— коэффициент теплообмена между греющей средой, соответственно с одной стороны, плитой, левый конец пластины 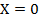 -теплоизолирован. Температуру греющей среды
-теплоизолирован. Температуру греющей среды 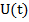 назовем управляющим воздействием или просто управлением. Для того, чтобы решение уравнения (1), (2) было однозначно определено, достаточно еще задать конечное или начальное распределение температуры
назовем управляющим воздействием или просто управлением. Для того, чтобы решение уравнения (1), (2) было однозначно определено, достаточно еще задать конечное или начальное распределение температуры 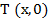 или
или 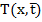 .
.
Однако, непосредственно приборами такое распределение температуры точно определить можно далеко не всегда. В процессе нагрева имеется возможность измерять изменения температуры в некоторых точках нагреваемого тела 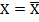 . Задача определения распределения температуры «стержня» на данный момент
. Задача определения распределения температуры «стержня» на данный момент 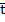 по известному изменению температуры
по известному изменению температуры 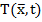 в точке
в точке 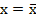 и законом теплопередачи (1)-(2) составляет предмет задачи идентификации (определения) процесса нагрева, рассматриваемой ниже.
и законом теплопередачи (1)-(2) составляет предмет задачи идентификации (определения) процесса нагрева, рассматриваемой ниже.
Функцию 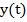 , связанную с распределением температуры
, связанную с распределением температуры 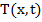 соотношением
соотношением
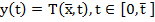 (3)
(3)
назовем измеряемой величиной процесса нагрева.
Задача 1. По функции 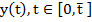 , константам
, константам 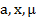 и соотношениям (1)-(3) определить
и соотношениям (1)-(3) определить 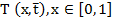 . Пуст
. Пуст 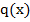 — некоторая заданная функция
— некоторая заданная функция 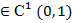 .
.
Задача 2. В условиях задачи 1 найти величину (проекцию).
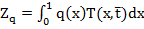 (4)
(4)
Понятно, что решение задачи 2 при различных функциях 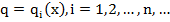 составляющих базис пространства
составляющих базис пространства 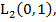 позволит найти функцию
позволит найти функцию 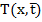 по проекциям (4) как элемент
по проекциям (4) как элемент 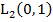 . По этому далее будем рассматривать только задачу 2.
. По этому далее будем рассматривать только задачу 2.
2. Условия идентифицируемости проекции.
Будем искать величину (4) в виде
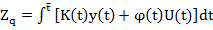 (5)
(5)
где 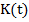 и
и 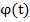 искомые функции из
искомые функции из 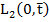 . Следуя известной технике теории наблюдаемости в линейных задачах (2, 3), выберем линейный функционал
. Следуя известной технике теории наблюдаемости в линейных задачах (2, 3), выберем линейный функционал 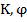 , так, чтобы при связи (1)-(3) выполнялось тождество
, так, чтобы при связи (1)-(3) выполнялось тождество
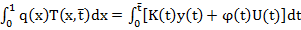 (6)
(6)
На решениях уравнения (1) образуем тождество
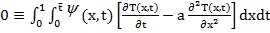 (7)
(7)
Здесь 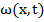 произвольная функция,
произвольная функция, 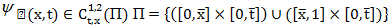 . Добавим гипотетическое тождество (6) к соотношению (7) и, пользуясь интегрированием по частям с учетом (2), (3), преобразуем полученное равенство к виду
. Добавим гипотетическое тождество (6) к соотношению (7) и, пользуясь интегрированием по частям с учетом (2), (3), преобразуем полученное равенство к виду
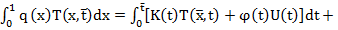
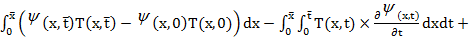
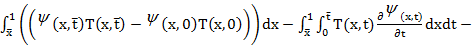
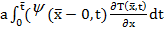
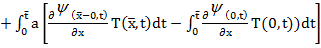 -
-
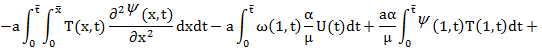
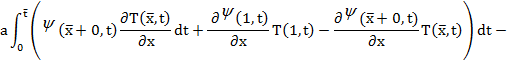
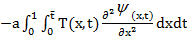 (8)
(8)
Теперь в (8) приравняем коэффициенты при 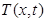 в левой и правой части. Это дает соотношение для
в левой и правой части. Это дает соотношение для 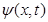 :
:
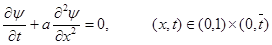 (9)
(9)
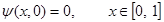 (10)
(10)
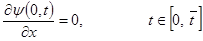 (11)
(11)
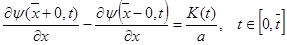 (12)
(12)
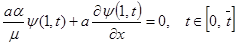 (13)
(13)
 (14)
(14)
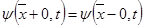 (14’)
(14’)
Итак, для функции 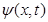 получена краевая задача (9)-(14’). Пусть она имеет решение при некоторой функции
получена краевая задача (9)-(14’). Пусть она имеет решение при некоторой функции 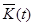 . Тогда в тождестве (8) остается
. Тогда в тождестве (8) остается
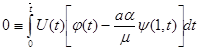
Отсюда заключаем: для того, чтобы выполнялось соотношение (6) при связях (1)-(3) и любом управлении 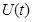 достаточно
достаточно
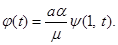 (1)
(1)
Итак, установлена теорема:
Для того, чтобы имело место тождество (6) при связях (1)-(3) достаточно, чтобы существовало решение краевой задачи (9)-(14’). При этом функции 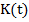 и
и 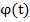 в (6) определяются решением этой задачи по связям (12)-(15).
в (6) определяются решением этой задачи по связям (12)-(15).
3. Вычислительные аспекты.
Решим задачу (9)-(14’) в случае 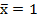 . Тогда равенства (12) и (13) преобразуются в условие
. Тогда равенства (12) и (13) преобразуются в условие
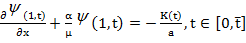 (15)
(15)
Теперь решим краевую задачу
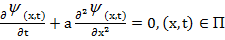 (9)
(9)
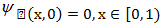 (10)
(10)
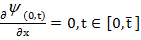 (11)
(11)
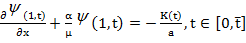 (14)
(14)
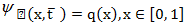 (15)
(15)
Пусть известно, что решение 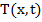 системы (1), (2) принадлежит множеству
системы (1), (2) принадлежит множеству 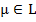 , где
, где 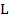 — линейное множество в
— линейное множество в 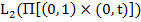 . Пусть управление
. Пусть управление 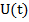 — известная функция. Возьмем некоторую функцию
— известная функция. Возьмем некоторую функцию 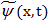 и
и 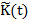 , приближенно удовлетворяющую условиям граничной задачи (9)-(11), (14), (15), т. е. возможны ненулевые невязки:
, приближенно удовлетворяющую условиям граничной задачи (9)-(11), (14), (15), т. е. возможны ненулевые невязки:
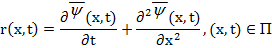
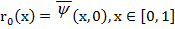
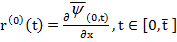 (16)
(16)
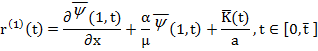
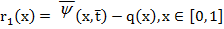 .
.
При таких 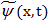 ,
, 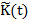 формула (6) имеет, согласно (8) погрешность
формула (6) имеет, согласно (8) погрешность
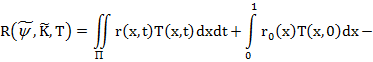
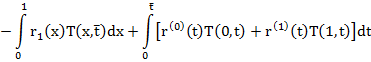
и оценку погрешности
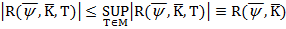
Таким образом, для повышения точности формулы (6) необходимо минимизировать величину 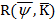 за счет выбора
за счет выбора 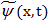 и
и 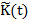 . Практический способ минимизации этой оценки можно выбрать в зависимости от множеств
. Практический способ минимизации этой оценки можно выбрать в зависимости от множеств 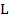 и
и 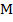 .
.
Пусть, например, 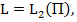 a
a 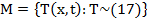 — множество непрерывных функций в
— множество непрерывных функций в 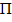 , удовлетворяющими неравенству.
, удовлетворяющими неравенству.
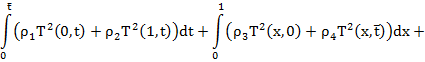
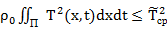 . (17)
. (17)
Тогда 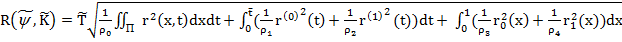
Минимизируем этот функционал по 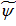 и
и 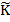 . Поскольку
. Поскольку 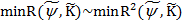 , то найдем
, то найдем
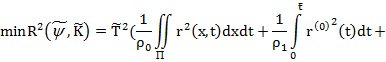
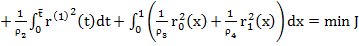 (17)
(17)
Прежде чем минимизировать 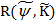 , положим
, положим
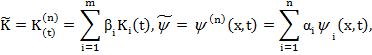
где 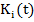 и
и 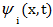 заданные системы базисных функций и обобщенные полиномы.
заданные системы базисных функций и обобщенные полиномы. 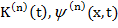 в (16), задачу минимума оценки (17) заменим задачей об экстремуме функций
в (16), задачу минимума оценки (17) заменим задачей об экстремуме функций 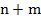 вещественных переменных
вещественных переменных 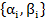 .
.
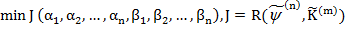
следуя методу разделения переменных (метод Фурье) в решении уравнения (9), построим функции
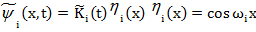 (18)
(18)
Функции (18) удовлетворяют условиям (9), (11) и будут удовлетворять (12) при
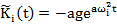 , где
, где 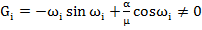 (19)
(19)
Теперь решение задачи (9), (11), (14), (15), в которой искомыми являются  и
и 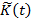 , можно строить в виде ряда по функциям (18):
, можно строить в виде ряда по функциям (18):
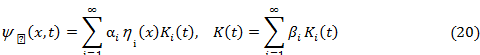
Заметим, что здесь можно выбрать коэффициенты 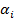 и частоты
и частоты 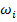 при соблюдении условия (19). Для функции (20)
при соблюдении условия (19). Для функции (20)
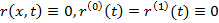 .
.
и оценка (17) принимает вид
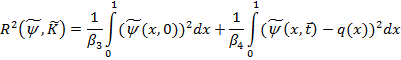
Ограничиваясь здесь отрезками 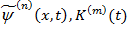 рядов (20) получим
рядов (20) получим
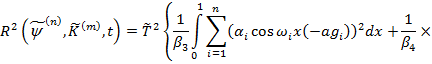
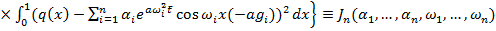 (21)
(21)
Теперь необходимо отыскивать минимум функции (21) по величинам 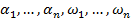 при условии (19). Найденное значение минимума будет давать оценку погрешности формулы (5).
при условии (19). Найденное значение минимума будет давать оценку погрешности формулы (5).
Считая число 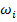 фиксированным, обозначим
фиксированным, обозначим
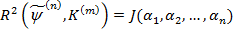
Необходимое условие экстремума этой функции 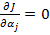 , т. е.
, т. е.
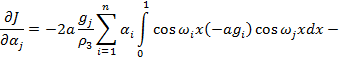
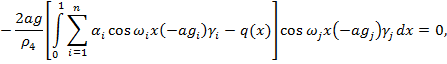
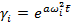 (18)
(18)
Примем
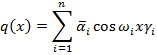
наложим условия
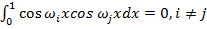 ,
,
которая очевидно выполняется при 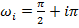 .
.
Тогда последнее равенство принимает вид
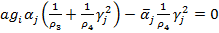 ,
,
отсюда
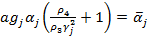 .
.
Итак  , где
, где 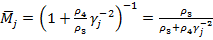
Представляя эти 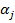 в (20) можем определить
в (20) можем определить 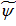 и
и 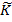 которые
которые
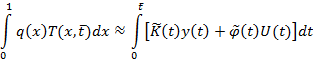
при связях (1)-(3) и функций 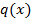 вида (18) обеспечивает приближенное равенство.
вида (18) обеспечивает приближенное равенство.
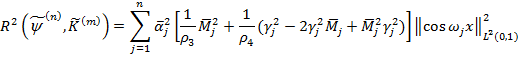
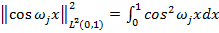 .
.
Таким образом, рассмотрели частный способ построения формулы (6). Если не требовать ортогональность системы 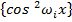 функции
функции 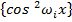 , то, как сказано выше, выбор
, то, как сказано выше, выбор 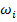 можно направить также как и коэффициент
можно направить также как и коэффициент 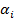 на минимизацию оценки (21). В этом случае следует ожидать существенно меньшего значения оценки. Такие задачи, подобно задаче построения квадратных формул типа Гаусса, если ограничиться подходящим классом функций
на минимизацию оценки (21). В этом случае следует ожидать существенно меньшего значения оценки. Такие задачи, подобно задаче построения квадратных формул типа Гаусса, если ограничиться подходящим классом функций 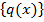 . Они, могут решаться численно. Заслуживает также внимания использование идеи метода максимизации проекций (3–5) для решения задачи 1.
. Они, могут решаться численно. Заслуживает также внимания использование идеи метода максимизации проекций (3–5) для решения задачи 1.
Литература:
1. Бутковский А. Т. Теория оптимального управления системами с распределенными параметрами. — М.: Наука, 1965. — 474 с.
2. Красовский Н. Н. Теория управления движением. — М.: Наука, 1968. — 476 с.
3. Кирин Н. Е. Методы последовательных оценок в задачах оптимизации управляемых систем. — Л.: изд-во ЛГУ, 1975. –160 с.
4. Иванов А. П., Кирин Н. Е. К методам наблюдения линейных возмущаемых систем. Дифференциальные уравнения. — 1974. — 10. — № 5. — С. 788–791.
5. Иванов А. П., Кирин Н. Е. Сопряжение задачи теории управления. — Л.: изд-во ЛГУ, 1988. — 88 с.

