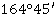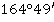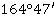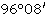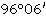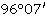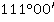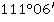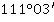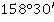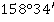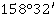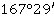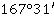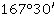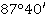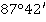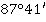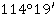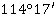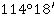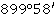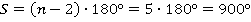Любые измерения сопровождаются неизбежными погрешностями. На примере теодолитной съёмки, проведенной студентами ПГУАС во время учебной геодезической практики и обработки полученных результатов, рассмотрим применение теории погрешностей в геодезических работах.
Изначально с помощью теодолита студенты измеряли внутренние углы в два приёма (при левом и правом круге теодолита). Затем с помощью среднего арифметического были получены окончательные значения углов (с помощью среднего арифметического получают наиболее надёжный результат из совокупности измерений одной и той же величины). Предположим, что было произведено n число равноточных измерений. Равноточными называются измерения, проведенные в одинаковых условиях, однотипными инструментами, одинаковое число раз, наблюдателями равной квалификации. Имеем:
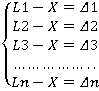
Просуммировав эти равенства, получим:
L1 + L2 + L3….. + Ln — nX = Δ1 + Δ2 + Δ3 …. + Δn (1)
Выразим
Х = 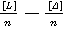
Допустим, что число измерений неограниченно велико (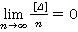 ):
):
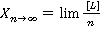 (2)
(2)
Из формулы (2) следует, что предел среднего арифметического при неограниченном числе измерений стремится к истинному значению величины. Но количество измерений всегда ограничено и вместо равенства мы имеем неравенство Х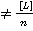 , отличающееся от равенства на очень малую величину, имеющую своим пределом 0.
, отличающееся от равенства на очень малую величину, имеющую своим пределом 0.
Введем понятие х — среднее арифметическое, тогда
х = 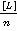 (3)
(3)
На основании формулы (3) можно утверждать, что среднее арифметическое из одинаково точных измерений, является наиболее точным результатом при любом числе измерений, если n> 1.
Таблица 1
Определение горизонтальных углов
|
№ точек теодолитного хода |
Значение угла при круге право |
Значение угла при круге лево |
Полученные углы, βu |
|
I |
|
|
|
|
II |
|
|
|
|
III |
|
|
|
|
IV |
|
|
|
|
V |
|
|
|
|
VI |
|
|
|
|
VII |
|
|
|
|
Сумма |
|
|
|
|
Теоретическая сумма |
|
|
|
Исходя из этих данных, погрешность измерений равна: 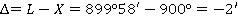 . Эта величина является угловой невязкой полигона. Данная невязка сравнивается с допустимой невязкой, которая определяется по формуле:
. Эта величина является угловой невязкой полигона. Данная невязка сравнивается с допустимой невязкой, которая определяется по формуле: 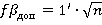 , где n–число углов полигона:
, где n–число углов полигона: 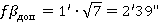 (
(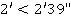 ). Полученная невязка, разносится равномерно на все углы полигона, с обратным знаком. Невязка отрицательная, значит она вносится со знаком +. Для удобства (чтобы не было значений углов с секундами) по
). Полученная невязка, разносится равномерно на все углы полигона, с обратным знаком. Невязка отрицательная, значит она вносится со знаком +. Для удобства (чтобы не было значений углов с секундами) по 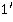 было добавлено в первый и четвёртый значения углов.
было добавлено в первый и четвёртый значения углов.
Далее студенты с помощью рулетки измеряли длины сторон полигона (т. е. горизонтальные проложения). Измерения производились дважды: в прямом и обратном направлении. Затем с помощью среднего арифметического рассчитывались итоговые значения.
Таблица 2
Расчёт значений длин сторон полигона
|
Обозначение линии |
Длина стороны в прямом направлении |
Длина стороны в обратном направлении |
Полученное горизонтальное проложение линии, di-k |
|
I-II |
74.70 |
74.10 |
74.40 |
|
II-III |
62.00 |
62.00 |
62.00 |
|
III-IV |
26.50 |
26.70 |
26.60 |
|
IV-V |
49.90 |
50.50 |
50.20 |
|
V-VI |
78.80 |
78.00 |
78.40 |
|
VI-VII |
54.00 |
52.60 |
53.30 |
|
VII-I |
64.10 |
64.50 |
64.30 |
На следующем этапе теодолитной съёмки студенты рассчитывали приращения координат с помощью горизонтальных проложений и дирекционных углов αi-k(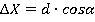 ,
, 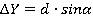 ). Сумма вычисленных приращений должна равняться 0.
). Сумма вычисленных приращений должна равняться 0.
В результате расчётов получились линейные невязки полигона по осям X и Y:
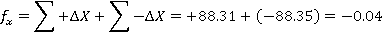
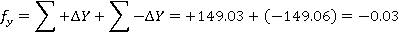
Абсолютная невязка полигона была определена по следующей формуле:
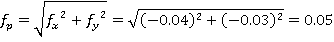
Для контроля правильности измерения полигона определим относительную невязку:
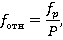
где 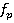 - абсолютная невязка полигона,
- абсолютная невязка полигона,
Р — периметр полигона (сумма горизонтальных проложений).
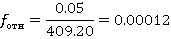
Для сравнения относительной невязки с допустимой, ее значение удобно преобразовать в простую дробь, числителем которой является 1: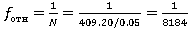 (для этого числитель и знаменатель делим на
(для этого числитель и знаменатель делим на 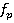 ). Сравниваем полученную относительную невязку, с допустимой (допустимая относительная невязка задается исходя из рельефа местности). В нашем случае 1/N =1/2000 (принимается как для твердой поверхности со спокойным рельефом). Сравнивая относительные невязки 1/Nпол=1/8184<1/Nдоп=1/2000 можно сделать вывод, что полученная невязка допустима,а значит измерения проведены правильно.
). Сравниваем полученную относительную невязку, с допустимой (допустимая относительная невязка задается исходя из рельефа местности). В нашем случае 1/N =1/2000 (принимается как для твердой поверхности со спокойным рельефом). Сравнивая относительные невязки 1/Nпол=1/8184<1/Nдоп=1/2000 можно сделать вывод, что полученная невязка допустима,а значит измерения проведены правильно.
Для того чтобы избавиться от полученных невязок в значения приращений координат вносятся поправки σx и σy(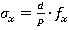 ,
, 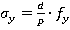 ). Суммы поправок равны невязкам и вносятся с обратным знаком (таблица 3).
). Суммы поправок равны невязкам и вносятся с обратным знаком (таблица 3).
Таблица 3
Результаты расчетов приращения координат
|
Обозначение линии |
Вычисленные приращения координат |
Поправки в приращении координат |
Исправленные приращения координат | |||
|
|
±∆Xb |
±∆Yb |
±σx |
±σy |
±∆Xур |
±∆Yур |
|
I-II |
9.99 |
-73.73 |
0.007 |
0.005 |
9.997 |
-73.725 |
|
II-III |
-60.20 |
-14.82 |
0.006 |
0.004 |
-60.194 |
-14.816 |
|
III-IV |
-15.21 |
21.82 |
0.003 |
0.002 |
-15.207 |
21.822 |
|
IV-V |
-11.66 |
48.83 |
0.005 |
0.004 |
-11.655 |
48.834 |
|
V-VI |
-1.28 |
78.38 |
0.008 |
0.006 |
-1.272 |
78.386 |
|
VI-VII |
53.28 |
-1.29 |
0.005 |
0.004 |
53.285 |
-1.286 |
|
VII-I |
25.04 |
-59.22 |
0.006 |
0.005 |
25.046 |
-59.215 |
|
|
∑+88.31 |
+149.03 |
|
|
∑+88.328 |
+149.042 |
|
|
∑-88.35 |
-149.06 |
|
|
∑-88.328 |
-149.042 |
|
|
fx =-0.04 |
fy =-0,03 |
|
|
|
|
После этого находим координаты всех точек теодолитного хода, прибавляя к исходной координате значения приращений координат с учетом их знака.
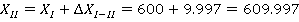
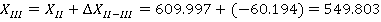
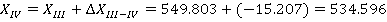
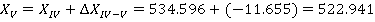
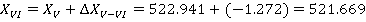
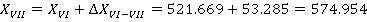
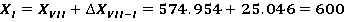
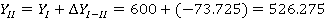
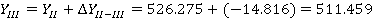
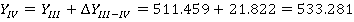
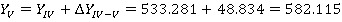
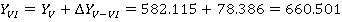
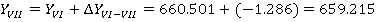
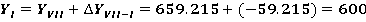
Так как полученные значения координат первой точки совпадают с исходными, то координаты точек полигона рассчитаны правильно.
Итак, при расчёте ведомости вычисления координат теодолитного хода использовались различные приёмы определения погрешностей измерений, оценки точности результатов измерений, уменьшения и устранения погрешностей измерений. Это нахождение вероятнейшего значения с помощью среднего арифметического, нахождение среднеквадратической погрешности, нахождение относительной погрешности, оценка точности функций измеренных величин. Таким образом, можно утверждать, что теория погрешностей имеет большое применение при осуществлении геодезических работ.
Литература:
1. Быкова Ю. С., Гафарова Д. З., Снежкина О. В. Прикладная математика в задачах геодезии // Современные научные исследования и инновации. 2014. № 12 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/12/42283