Технология выращивания квантовых проволок может сопровождаться возникновением дефектов упаковки и краевых дислокаций. Последние играют существенную роль в рассеянии носителей заряда при достаточно низких температурах, а следовательно, оказывают значительное влияние на транспортные свойства квантовых проволок. Во внешнем продольном магнитном поле появляются новые возможности для управления подвижностью носителей заряда в квантовой проволоке, что важно для приложений в полупроводниковой наноэлектронике.
Цель работы заключается в теоретическом исследовании влияния краевой дислокации на подвижность электронов в квантовой проволоке во внешнем продольном магнитном поле, а также в сравнении с влиянием другим механизмом рассеяния, рассмотренных ранее в работах [1, 2].
Рассмотрим полупроводниковую квантовую проволоку (КП) находящуюся в продольном по отношению к ее оси магнитном поле. Будем считать, что КП имеет форму круглого цилиндра, радиус основания 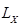 которого значительно меньше его длины
которого значительно меньше его длины 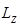 (
(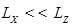 ). Предположим, что дислокация ориентирована вдоль оси y в плоскости поперечного сечения КП, а рассеяние электронов происходит в плоскости xz (рис. 1).
). Предположим, что дислокация ориентирована вдоль оси y в плоскости поперечного сечения КП, а рассеяние электронов происходит в плоскости xz (рис. 1).
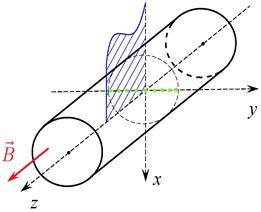
Рис. 1. КП с краевой дислокацией во внешнем магнитном поле
Векторный потенциал магнитного поля 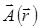 выберем в симметричной калибровке
выберем в симметричной калибровке 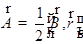 , так что
, так что 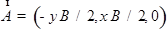 ,
, 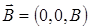 .
.
Потенциал конфайнмента КП моделируется потенциалом двумерного гармонического осциллятора:
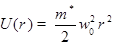 , (1)
, (1)
где 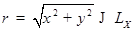 ;
; 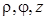 — цилиндрические координаты;
— цилиндрические координаты; 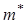 — эффективная масса электрона;
— эффективная масса электрона; 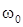 — характерная частота удерживающего потенциала.
— характерная частота удерживающего потенциала.
Как известно [3], краевые дислокации в полупроводниках с долей ковалентной связи действуют как акцепторные центры, поэтому в кристаллах n-типа дислокационная линия становится отрицательно заряженной и вокруг нее образуется область положительного заряда. Налетающие на дислокацию электроны испытывают с ее стороны отталкивание, приводящее к их рассеянию и тем самым уменьшению подвижности.
Согласно модели Бонч-Бруевича и Когана, экранированный потенциал заряженной дислокации имеет вид [3]
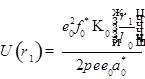 , (2)
, (2)
где 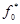 — вероятность заполнения акцепторного центра в дислокационной линии;
— вероятность заполнения акцепторного центра в дислокационной линии; 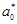 — расстояние между акцепторными центрами в дислокационной линии; ε — диэлектрическая проницаемость материала КП;
— расстояние между акцепторными центрами в дислокационной линии; ε — диэлектрическая проницаемость материала КП; 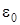 — электрическая постоянная;
— электрическая постоянная; 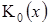 — функция Макдональда;
— функция Макдональда; 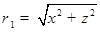 ,
, 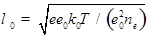 — длина экранирования Дебая,
— длина экранирования Дебая, 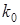 — постоянная Больцмана, Т — температура,
— постоянная Больцмана, Т — температура, 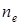 — концентрация электронов в КП.
— концентрация электронов в КП.
Ограничиваясь вкладом основной подзоны размерного квантования для подвижности носителей тока в КП получим [4]
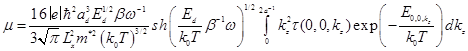 , (3)
, (3)
где 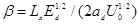 ;
; 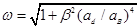 ;
; 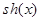 — гиперболический синус;
— гиперболический синус; 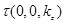 — время релаксации носителей заряда в КП;
— время релаксации носителей заряда в КП; 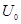 — амплитуда потенциала конфайнмента;
— амплитуда потенциала конфайнмента; 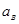 — магнитная длина;
— магнитная длина; 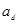 и
и 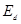 — эффективный боровский радиус и энергия соответственно;
— эффективный боровский радиус и энергия соответственно; 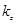 — проекция квазиволнового вектора электрона в КП на ось Оz.
— проекция квазиволнового вектора электрона в КП на ось Оz.
На рис. 2 представлены температурные зависимости подвижности электронов в GaAs КП при рассеянии на LA-фононах [1] (кривая 1), на флуктуациях толщины КП [2] (кривая 2) и на краевой дислокации согласно (3) для параметров GaAs [2]: плотность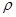 = 5.3·103 кг/м3, продольная скорость звука v = 5.2·103 м/с, константа деформационного потенциала С = 2.2·10–18 Дж, корреляционный радиус
= 5.3·103 кг/м3, продольная скорость звука v = 5.2·103 м/с, константа деформационного потенциала С = 2.2·10–18 Дж, корреляционный радиус 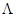 =1·10–8 м [2].
=1·10–8 м [2].
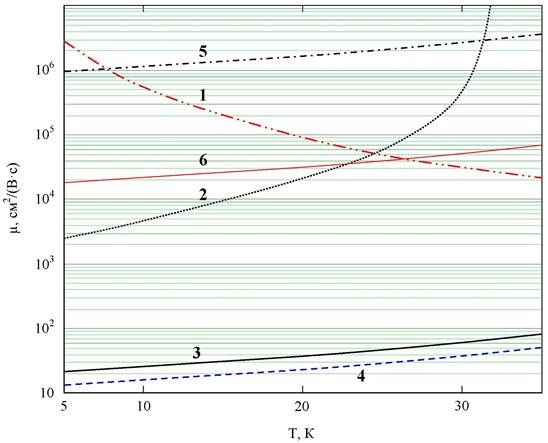
Рис. 2. Температурная зависимость подвижности электронов в GaAs КП при 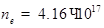 см–3; 2LX = 7 нм; LZ = 1 мкм;
см–3; 2LX = 7 нм; LZ = 1 мкм; 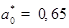 нм;
нм; 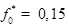 , для различных механизмов рассеяния: 1 — рассеяние на LA-фононах [1]; 2 — рассеяние на флуктуациях толщины КП [2]; 3–6 — рассеяние на краевой дислокации (кривые 1–3, 5–6 построены при В = 0 Тл; кривая 4 при В = 2 Тл, кривая 5 построена при
, для различных механизмов рассеяния: 1 — рассеяние на LA-фононах [1]; 2 — рассеяние на флуктуациях толщины КП [2]; 3–6 — рассеяние на краевой дислокации (кривые 1–3, 5–6 построены при В = 0 Тл; кривая 4 при В = 2 Тл, кривая 5 построена при 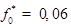 , кривая 6 при
, кривая 6 при 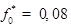 )
)
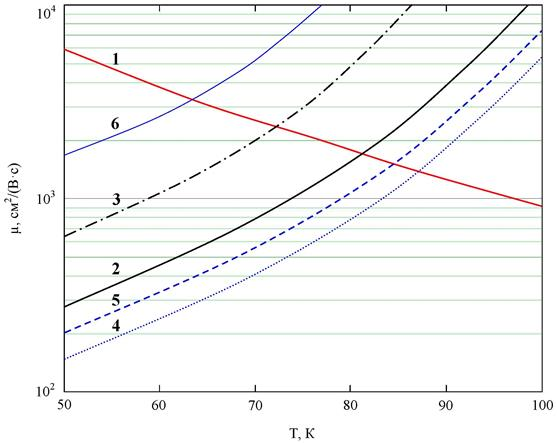
Рис. 3. Температурная зависимость подвижности электронов в GaAs КП при 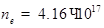 см–3; 2LX = 7 нм; LZ = 1 мкм: 1 — рассеяние на LA-фононах [1]; 2–6 — рассеяние на краевой дислокации (кривые 1–3, 6 построены при В = 0 Тл; кривая 5 при В = 2 Тл) для различных значений параметров дислокационной линии
см–3; 2LX = 7 нм; LZ = 1 мкм: 1 — рассеяние на LA-фононах [1]; 2–6 — рассеяние на краевой дислокации (кривые 1–3, 6 построены при В = 0 Тл; кривая 5 при В = 2 Тл) для различных значений параметров дислокационной линии 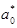 и
и 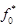 :
:
2 — 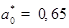 нм;
нм; 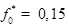 ;
;
3 — 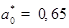 нм;
нм; 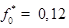 ;
;
4 — 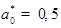 нм;
нм; 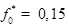 ;
;
5 — 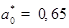 нм;
нм; 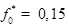 ;
;
6 — 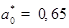 нм;
нм; 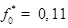
Из рис. 2 следует, что вклад механизма релаксации связанного с рассеянием электронов на краевой дислокации зависит от величины параметра 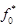 — вероятности заполнения акцепторных центров в дислокационной линии (сравн. кривые 5 и 3). При
— вероятности заполнения акцепторных центров в дислокационной линии (сравн. кривые 5 и 3). При 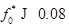 данный механизм в области температур от 5 до 30 К может быть существенным в сравнении с рассеянием на акустических фононах и на случайных неровностях границ КП (сравн. кривые 1, 2 и 3). В области температур от 50 до 100 К рассмотренный механизм становится эффективным по сравнению с рассеянием на LA-фононах при
данный механизм в области температур от 5 до 30 К может быть существенным в сравнении с рассеянием на акустических фононах и на случайных неровностях границ КП (сравн. кривые 1, 2 и 3). В области температур от 50 до 100 К рассмотренный механизм становится эффективным по сравнению с рассеянием на LA-фононах при 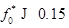 (сравн. кривые 1 и 4 на рис. 3). В магнитном поле подвижность электронов уменьшается за счёт сжатия электронной волновой функции в радиальной плоскости КП (сравн. кривые 3 и 4 на рис. 2 и кривые 5 и 4 на рис. 2).
(сравн. кривые 1 и 4 на рис. 3). В магнитном поле подвижность электронов уменьшается за счёт сжатия электронной волновой функции в радиальной плоскости КП (сравн. кривые 3 и 4 на рис. 2 и кривые 5 и 4 на рис. 2).
Литература:
1. Поклонский, Н. А. О температурной зависимости статической электропроводности полупроводниковой квантовой проволоки в изоляторе. / Н. А. Поклонский, Е. Ф. Кисляков, С. А. Вырко // ФТП. — 2003. — Т. 37. — Вып. 6. — С. 735
2. Рувинский, М. А. О влиянии флуктуаций толщины на статическую электропроводность квантовой полупроводниковой проволоки. / М. А. Рувинский, Б. М. Рувинский // ФТП. — 2005. — Т. 39. — Вып. 2. — С. 247.
3. Бонч-Бруевич, В. Л. К теории электронной плазмы в полупроводниках. / В. Л. Бонч-Бруевич, С. М. Коган // ФТТ. — 1959. — Т.1 — Вып. 8. — С. 1221.
4. Кревчик, В. Д. Подвижность электронов в квантовой проволоке с краевой дислокацией во внешнем магнитном поле. / В. Д. Кревчик, В. Н. Калинин, Е. Н. Калинин // Известия высших учебных заведений. Поволжский регион. Физико-математические науки. — 2014. — № 1 (29). — С. 70–84.

