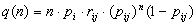Рассмотрено стохастическое представление процесса цепной сополимеризации с учетом инициирования и обрыва, который подчиняется марковской статистике. Получены зависимости среднечисленного молекулярно-массового распределения от степени полимеризации и переходных вероятностей при росте макроцепи.

Ключевые слова: сополимеризация, стохастическая модель роста макроцепи, молекулярно-массовое распределение.

Реакционная способность активных центров на концах макроцепи, при рассмотрении процесса ее формирования, в большинстве случаев определяется природой последнего звена. С точки зрения классической кинетической модели это представляется следующим образом 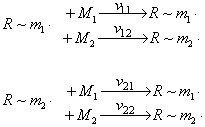[1]:

                                                                                                (1)

где R ~ m₁· и R ~ m₂· – активные центры макромолекулы, оканчивающиеся мономерами М₁ и М₂. Каждый акт присоединения мономера характеризуется скоростью протекания реакции v_ij (i, j = 1, 2).

 При этом составы сополимера и мономерной смеси связаны известным уравнением Майо-Льюиса [2]:

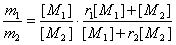
где [М₁] и [М₂] – концентрации мономеров М₁ и М₂, m₁ и m₂ – концентрации звеньев в сополимере, r₁ и r₂ – относительные активности мономеров.

Модель построения цепи может быть представлена в стохастическом виде [3, 4, 5]. В этом случае вместо скоростей элементарных актов роста рассматриваются вероятности перехода активного центра из i-го состояния в j-ое – p_ij. При этом мы нивелируем принятые по умолчанию приближения относительно первого порядка протекания реакций роста цепи по активному центру и по мономеру, а также условие стационарности. Также существенным отличием стохастического описания от кинетического является то, что его модельные параметры инвариантны относительно реального времени. То есть время в этом подходе измеряется не секундами или каким-либо другими периодами гармонического колебания, а числом актов присоединения.

В случае стохастического описания последовательности актов присоединения описываются показательной функцией (p_ij)ⁿ. Для учета инициирования и обрыва цепи необходимо ввести во множество событий присоединений соизмеримую оценку процессов возникновения радикалов и их гибели.

Будем считать, что после присоединения второго мономера к инициатору мы уже не различаем структуры макрорадикала дальше концевого звена. Гибель радикала может происходить на стадиях инициирования, первоначального и последующего роста цепи. Общую схему процесса инициирования, роста и обрыва цепи в концевой модели сополимеризации можно представить в виде набора уравнений следующих переходов:

-       инициирование

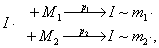
-       рост цепи

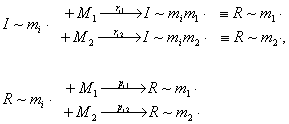
-       обрыв цепи

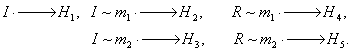
Здесь I× – инициирующий активный центр, p_i – вероятности присоединения к I× мономера М_i; r_ij – вероятность присоединения второго мономерного звена, p_ij – вероятность перехода состояния R~m_i в R~m_j·, или вероятность присоединения мономера M_j к R~m_i (i ,j = 1, 2); H₁, H₂, H₃, H₄, H₅ – состояния гибели радикала на различных стадиях роста макроцепи.

То же самое можно изобразить в виде дерева событий, на котором выделен путь образования цепи Im₂m₁m₂m₁m₂m₂m₁H₄ (рис. 1).

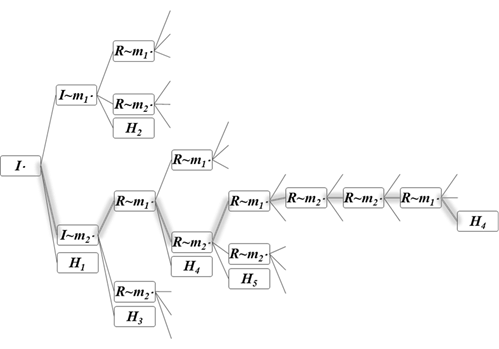
Рис. 1. Дерево событий при росте полимерной цепи

В теории конечных цепей Маркова полный процесс представляется с помощью канонической формы матрицы переходных вероятностей [5, 6]. Каноническая форма матрицы на примере сополимеризации m₁ и m₂ имеет следующий вид (рис. 2).

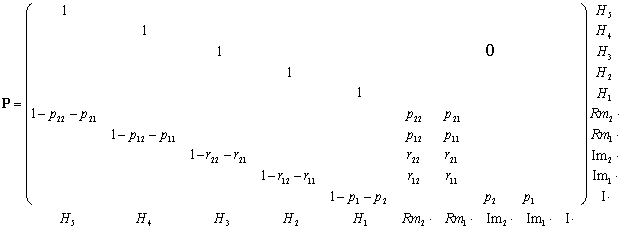
Рис. 2. Каноническая форма матрицы переходных вероятностей при сополимеризации m₁ и m₂ с учетом инициирования и обрыва

В данной матрице справа указаны начальные состояния элементарных актов процесса сополимеризации, а внизу – состояния, в которые он в результате попадает.

В этом случае есть возможность представить стохастическое описание среднечисленного молекулярно-массового распределения q(n) в зависимости от степени полимеризации n.

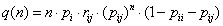
Если не рассматривать суперпозицию процессов роста по отношению к актам инициирования и различным вариантам гибели макрорадикала, то вид этой зависимости достаточно сложен. Результатом может быть молекулярно-массовое распределение с некоторым количеством экстремумов.

Рассмотрим возможность укрупнения (объединения, свёртки) процессов инициирования, роста и обрыва.

В этом случае общая зависимость будет описываться функцией:

Если считать, что инициирование привело к образованию состояний более чем с двумя звеньями, т.е. p_i = r_ij = 1, то выражение преобразуется в:

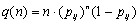
Графически данная зависимость при различных вероятностях роста цепи показана на рис. 3.

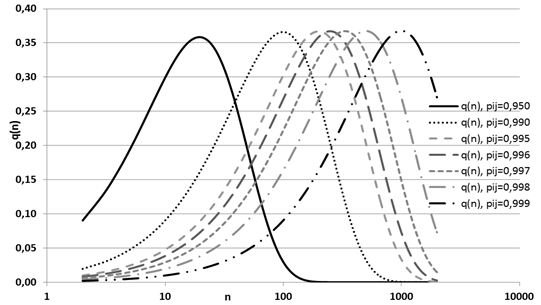
Рис. 3. Рассчитанное молекулярно-массовое распределение сополимера в зависимости от степени полимеризации и переходных вероятностей при росте макроцепи

Полученные зависимости очень похожи на классические функции молекулярно-массового распределения [7], что говорит о возможности применения канонической формы матрицы переходных вероятностей для описания цепных полимеризационных процессов с учетом инициирования, роста, обрыва цепи и других факторов.

Литература:

1.      Шур А.М. Высокомолекулярные соединения. 3 изд. М.: Высшая школа, 1981. – 656 с.

2.      Mayo F.R., Lewis F.M. Copolymerization. I. A Basis for Comparing the Behavior of Monomers in Copolymerization; The Copolymerization of Styrene and Methyl Methacrylate // J. Am. Chem. Soc. 1944. V. 66. № 9. P. 1594–1601.

3.      Price F.P. Copolymerization Mathematics and the Description of Stereoregular Polymers // J. Chem. Phys. 1962. V. 36. № 1. P. 209–218.

4.      Koenig J.L. Chemical Microstructure of Polymer Chains. New York: Wiley, 1982. 414 p.

5.      Ловчиков В.А. Автореф. … канд. хим. наук. Л.: ВНИИСК, 1982.

6.      Кемени Д.Д., Снелл Д.Л. Конечные цепи Маркова. М.: Наука, 1970. – 272 с.

7.      Flory P.J. Molecular size distribution in linear condensation polymers // J. Am. Chem. Soc. 1936. V. 58. № 10. P. 1877–1885.