В работе рассматривается неразрушающий контроль теплофизических свойств твердых материалов с использованием периодического нагрева. Обоснованы два варианта задания теплового воздействия, подчиняющихся гармоническим законам изменения плотности теплового потока.
Ключевые слова: неразрушающий контроль, периодический нагрев, тепловой анализ, теплофизические свойства, твердые материалы.
Одним из приоритетных направлений развития экономики страны является энергосбережение. Оно в 2...5 раз выгоднее, чем строительство новых мощностей по производству тепловой и электрической энергии [1]. Напрямую с энергосбережением связана разработка методов и средств определения комплекса теплофизических свойств (ТФС) материалов.
В случае неразрушающего контроля (НК) активными тепловыми методами искомые ТФС проявляются через температурный отклик (термограмму) исследуемого объекта на тепловое воздействие, которому он подвергается в специально организованном эксперименте [2, 3].
Тепловые воздействия постоянной мощности от плоского и от импульсного линейного нагревателя источников тепла широко используются в методах НК теплофизических свойств твердых материалов [4–7].
Метод периодического нагрева позволяет исследовать широкий класс явлений, проявляющихся в особенностях тепловых свойств веществ [8]. Моделирование теплопереноса в системе двух тел при гармоническом тепловом воздействии детально представлено в работе [9].
В данной работе рассмотрены два варианта задания теплового воздействия, подчиняющегося гармоническим законам изменения плотности теплового потока. Первый случай — тепловой поток содержит только периодическую составляющую. Во втором варианте тепловой поток содержит периодическую и постоянную составляющие.
Первый случай. На поверхность полуограниченного тела, которое представляет собой исследуемое изделие из твердого материала, действует тепловой источник, плотность теплового потока (q) которого изменяется по гармоническому закону:
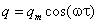(1)
Изменение температуры Tобщот времени τ в любой точке может быть записано в виде:
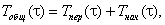(2)
где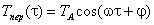 
– периодическая составляющая, Tнач(τ) — монотонная, стремящаяся к нулю функция, зависящая от начальных условий, TA — амплитуда изменения температуры.
Рассмотрим определенный интеграл за один период изменения Tобщ.
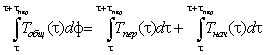(3)
Здесь: τпер — период гармонических колебаний. Значение интеграла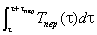 
будет равно нулю, т. к.
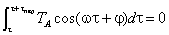. Значение интеграла
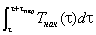будет стремиться к нулю при 
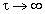, так как с течением времени влияние начального распределения температуры перестает проявляться.
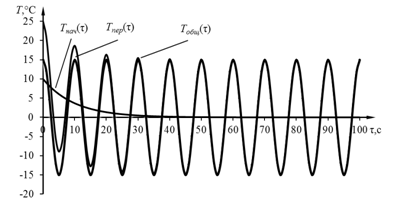
Рис. 1. Изменение температуры во времени для первого случая задания теплового воздействия
В реальном эксперименте значения температуры Ti измеряются через заданный промежуток времени Δτ. В связи с этим значение интеграла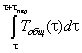 
рассчитываем численным способом по методу трапеций. Площадь под участком кривой за период
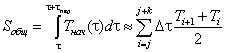(4)
Здесь: j=1..., n — k; n — число экспериментально полученных значений температуры,
k — число экспериментальных значений температуры в периоде.
При Sобщ= 0 начальное распределение температуры перестает влиять на изменение температурного поля, т. е. система выходит на квазистационарный режим.
Второй случай. Для создания гармонического теплового воздействия предлагается использовать элемент Пельтье, который позволяет проводить эксперименты при температуре выше или ниже температуры термостатирования. В этом случае кроме периодической составляющей будет присутствовать постоянная составляющая теплового потока. Зависимость плотности теплового потока от времени будет иметь вид: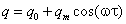 
. В этом случае изменение температуры:
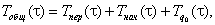(5)
где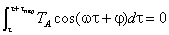 
— периодическая составляющая; Tнач(τ) — монотонная, стремящаяся к нулю функция, зависящая от начальных условий, 
– монотонно изменяющаяся функция, зависящая от начального теплового потока q0. Функция монотонно возрастает при q0 > 0 и монотонно убывает при q0 < 0.
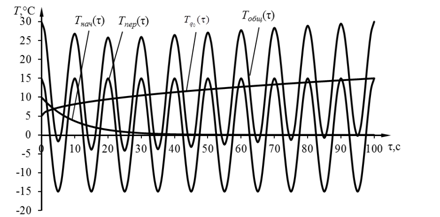
Рис. 2. Изменение температуры во времени для второго случая задания теплового воздействия
Рассмотрим определенный интеграл:
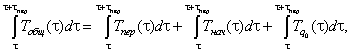(6)
Значение интеграла 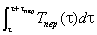будет равно нулю, т. к. 
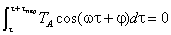. Значение интеграла 
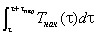будет стремиться к нулю при 
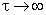. Значение интеграла 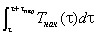будет монотонно изменяться с течением времени, уменьшаясь или увеличиваясь в зависимости от знака q0.
В соответствии с теоремой о среднем, если функция f(τ) непрерывна на отрезке [с;p], то на этом отрезке найдется хотя бы одна точка m, для которой справедливо равенство:
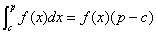. (7)
Если изменение монотонно возрастающей или убывающей функции на отрезке [c; p] незначительно, то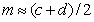 
. Для нашего случая условием выполнения равенства будет 
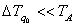, где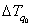 
– изменение 
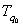за период τпер. Тогда в соответствии с уравнением (7) получим:
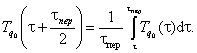(8)
В реальном эксперименте температура измеряется через заданный промежуток времени Δτ. В связи с этим интеграл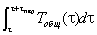 
рассчитываем численным способом по методу трапеций:
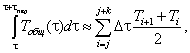(9)
где j=l..., n — k, n — число всех экспериментальных значений температуры, k — число экспериментальных значений температуры в периоде, l — номер точки, с которой начинается квазистационарная стадия и выполняется условие .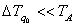
Уравнение (8) примет вид:
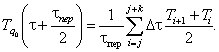(10)
Для выделения периодической составляющей из Tобщ(τ) вычитаем 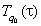. На начальном участке (до значения τl) не выполняется условие 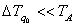, влияние начального распределения температуры существенно. Процедура нахождения квазистационарной стадии аналогична процедуре, рассмотренной в первом случае.
Таким образом, алгоритм определения периодической составляющей состоит из:
- построения зависимости 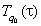в соответствии с выражением (9);
- вычитания из Tобщ(τ) зависимости;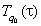
- определения начала квазистационарной стадии по условию Sобщ=0.
Литература:
1. Рудобашта С. П. Теплотехника — М.:КолосС, 2010. — 599 с.
2. Жуков Н. П., Майникова Н. Ф. Многомодельные методы и средства не-разрушающего контроля теплофизических свойств твердых материалов и изделий. М.: Изд-во Машиностроение-1. 2004. 288 с.
3. Многомодельные методы в микропроцессорных системах неразрушающего контроля теплофизических характеристик материалов: учебное пособие/ С. В. Мищенко, Ю. Л. Муромцев, Н. П. Жуков, Н. Ф. Майникова, И. В. Рогов, О. Н. Попов; под ред. С. В. Мищенко. — Тамбов: изд-во ФГБОУ ВПО «ТГТУ», 2012. –112 с.
4. Моделирование процесса теплопереноса от плоского источника тепла постоянной мощности при теплофизических измерениях/ Н. П. Жуков, Н. Ф. Майникова. — Инженерно-физический журнал, 2005. — Т. 78, № 6, с. 5–63.
5. Определение условий адекватности модели распределения тепла в плоском полупространстве реальному процессу при теплофизическом контроле/ Н. Ф. Майникова, Н. П. Жуков, А. А. Балашов, С. С. Никулин. — Вестник Тамбовского государственного технического университета, 2006.–Т. 12, № 3–1. — с. 610–616.
6. Моделирование процесса теплопереноса от импульсного линейного источника тепла при теплофизических измерениях/ Н. П. Жуков, Ю. Л. Муромцев, Н. Ф. Майникова, И. В. Рогов, — Вестник Тамбовского государственного технического университета, 2002.–Т. 8, № 2. — с. 182–189.
7. Теоретическое обоснование метода неразрушающего контроля теплофизических свойств материалов/ Н. П. Жуков, Н. Ф. Майникова, И. В. Рогов, О. Н. Попов, — Вестник Тамбовского государственного технического университета, 2010.–Т. 16, № 2. — с. 296–302.
8. Рожков А. В. Измерительная система для определения теплофизических свойств материалов методом периодического нагрева / Проблемы техногенной безопасности и устойчивого развития. Сборник научных статей молодых ученых, аспирантов и студентов /ФГБОУ ВПО «ТГТУ». — Тамбов: Изд-во ФГБОУ ВПО «ТГТУ», 2013. — Вып.IV — c. 26–29.
9. Моделирование теплопереноса в системе двух тел при гармоническом тепловом воздействии / И. В. Рогов, Н. Ф. Майникова, С. В. Молодов, О. Н. Попов // Вестник Тамбовского государственного технического университета. — 2011. — Т. 17, № 2. — С. 360–364.
