Испытание материалов локальным деформированием



Рассматривается метод испытания материалов локальным деформированием на основе теории механики деформируемого твердого тела.

Ключевые слова:метод испытаний, локальное деформирование, модель материала, напряженное состояние

Введение. Метод локального деформирования (МЛД) есть квазистатический метод испытаний материалов механическим воздействием на участок поверхности, значительно меньший размеров всего тела, с измерением силового контактного взаимодействия и перемещений границы контакта вплоть до разрушения материала. Такое деформирование материала позволяет получить о материале большую информацию, чем испытание по методу твердости.

Подобные методы давно нашли практическое применение благодаря простой реализации без сложного и громоздкого оборудования [1]. Актуальность заключается в необходимости дальнейшей разработки таких безобразцовых испытаний деформационно-прочностных характеристик материалов изделий в процессе изготовления, хранения и эксплуатации (всего жизненного цикла изделия). Основной проблемой при этом является повышение точности методик, применяемых в подобных испытаниях материалов.

Практическая значимость этого метода заключается в уменьшении затрат на изготовление образцов-спутников, на которых традиционно определяются деформационно-прочностные характеристики материала изделий, так как само изделие является образцом, а также возможность оценки напряженного состояния элементов конструкций.

Основные требования кметодикам подобного типа заключаются вследующем:

следуемого материала; стям измерений и вычислений;

возможность простой технической реализации методики.

Новизна данного подхода состоит в методологии, позволяющей из множества схем нагружения участка поверхности выбрать такие, которые при наименьшем количестве измеряемых с приемлемой точностью величин позволяют реализовать наиболее устойчивый алгоритм вычислений значений требуемых характеристик.

Подход основывается на физико-механической модели материала, предполагающей нелинейную функциональную связь напряжений и деформаций, материальные функции и константы которой определяются для испытуемого изделия. Постановка задачи. Задача формулируется с позиций механики деформируемого твердого тела. Предполагается, что процесс деформирования квазистатический, поэтому время t входит параметром. Деформирование производится при постоянной температуре Т. Система уравнений включает уравнение равновесия для испытуемого материала

связь перемещений с деформациями

Напряжения и деформации представляются функциональной зависимостью из-за возможной сложности физической модели материала

где учитывается анизотропия деформационных характеристик материала, наличие начальных напряжений в материале, неоднородность механических свойств в разных точках тела, возможность влияния предшествующей истории нагружения (вязкоупругое поведение материала), влияние температуры и других параметров (физических, геометрических и др.) на связь σ ~ ε.

Зависимость σ ~ ε’ является определяющей для формирования способа испытаний и соответственно для граничных условий, замыкающих математическую постановку задачи. Так, для испытания изотропных материалов можно использовать осесимметричные инденторы, тогда как для анизотропных материалов более подходят инденторы, имеющие в сечении эллипсоидальную форму. Для испытания массивного тела можно использовать аналитические решения контактных задач для полупространства, тогда как для испытаний материалов пластинчатых изделий нужно учитывать их толщину.

Важным моментом является неоднородность материала у разных областей поверхности тела и в зависимости от глубины залегания под поверхностью. Это влияние проявляется по разной реакции материала в различных зонах поверхности тела. Отличие физико-механических характеристик поверхностных слоев от глубинных проявляется в нарушении подобия зависимости силы сопротивления от глубины вдавливания при испытаниях вдавливанием жестких инденторов.

МЛД применим также для определения напряженности элементов конструкций.

3. Граничные условия. Приведенная выше система уравнений механики деформируемого твердого тела дополняется граничными условиями. Для МЛД предпочтительным является такая форма наконечника индентора при вдавливании, для которой в «отклике материала» на деформирование поверхности вклад напряженной зоны был определяющим. Это важно для корректности обратной задачи и алгоритма определения материальных параметров моделей, описывающих нелинейные эффекты деформирования, проявляющиеся в наиболее напряженной зоне. Для МЛД также желательным является неизменность размеров области контакта с поверхностью материала в процессе испытания, чтобы начальный этап зависимости сопротивления от деформирования был линейным.

Предполагается, что контактная область S поверхности материала при испытании остается постоянной. В этой зоне точкам поверхности задаются перемещения.

В остальных точках поверхности задается нормальное давление и отсутствие касательных поверхностных нагрузок

4. Вариационная постановка задачи. Система уравнений (1) — (5) эквивалентна функциональному уравнению на основе принципа виртуальных работ

где δω иδu вариации перемещений точек контактной поверхности, соответствующие перемещениям индентора сцепленного с поверхностью материала в поверхности контакта; σ_п и τ — нормальное и касательное напряжения на контактной поверхности.

Говоря о граничных условиях, следует учитывать случай испытания листовых материалов. В этом случае нужно учитывать тыльную граничную поверхность листового материала, в точках которой следует задать нулевые перемещения при полном сцеплении с жестким опорным телом или учесть проскальзывание.

Для определения конкретных значений материальных констант физико-математической модели материала нужно иметь такое же количество независимых испытаний. То есть, выбирая физико-математическую модель, нужно планировать такое количество независимых способов деформирования материала, сколько материальных констант и параметров модели нам нужно получить в итоге. При этом для каждого способа испытаний желательно иметь аналитическое решение соответствующей краевой задачи. Полученная система должна иметь хорошо обусловленную матрицу, иначе погрешности экспериментальных измерений не позволят получить искомые значения с требуемой точностью.

5. Пример реализации МЛД. Рассмотрим реализациюМЛД для определения упругих констант эластичного резиноподобного материала. В этом случае связь напряжений с деформациями имеет вид

где G и v — модуль сдвига и коэффициент Пуассона.

Общеизвестным является метод вдавливания индентора в поверхность исследуемого материала. При этом можно рассматривать различные условия сцепления в зоне контактного взаимодействия. Использование только этого вида деформирования поверхностного слоя материала позволяет построить методику определения упругих характеристик материалов: модуля упругости и коэффициента Пуассона [2]. Однако эта методика неэффективна, например, для малосжимаемых материалов [3], у которых значение коэффициента Пуассона близко к 0.5. Тогда как достаточно точное определение величины коэффициента Пуассона таких материалов важно для прикладных задач.

Стремление разработать способ локального деформирования устойчивый к погрешностям испытаний привело к совмещению вдавливания и закручивания контактной поверхности. Использование закручивания площадки контакта исследуемого материала индентором предполагает соответствующее решения задачи теории упругости[3]. Это решение дает зависимость закручивающего момента, действующего на цилиндрический индентор радиусаα,от модуля упругости материала полупространства и угла закручивания

Дополнив это соотношение зависимостью силы, вдавливающей цилиндрический индентор в упругое полупространство, от глубины вдавливания

и зависимостью между упругими константами

получим систему уравнений для определения упругих констант материала.

Решив систему, получим следующие выражения для коэффициента Пуассона и модуля упругости

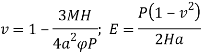
Экспериментальная проверка этого способа показала [3] следующее. В отличие от других методик не возникает затруднений при вычислении значений коэффициентов Пуассона слабосжимаемых материалов. Кроме этого точность определения коэффициента Пуассона оказалась на порядок выше, чем при одноосном растяжении.

Таким образом, видно, что учет всех требований подхода и, прежде всего, сочетание двух существенно различных видов деформирования позволяет получить устойчивый алгоритм и эффективную методику определения упругих констант МЛД.

6. Применение МЛД для определения основных деформационных свойств материалов. В приведенном выше подходе предполагается, что выбор модели материала сделан заранее на основе информации о деформационных свойствах материала. Однако практический интерес представляет подход, когда конкретный вид модели заранее не определен и выявляется в процессе испытаний материала изделий. При этом предполагается, что имеются достаточные участки свободной поверхности твердого тела, на которые можно осуществлять контактное силовое воздействие, и что размер зоны контакта значительно меньше размеров свободной поверхности.

Возможен следующий алгоритм применения МЛД:

1. Проверка изотропности деформационных свойств вдоль поверхностных слоев вдавливанием по нормали к поверхности инденторов с плоским эллиптическим вытянутым в плане основанием. Для близких значений глубины вдавливания с постоянной силой (в пределах погрешности измерений) при различных углах поворота индентора делается заключение об изотропности поверхностного слоя тела. В противном случае дальнейшие испытания следует проводить только с эллиптическим индентором.
2. Проверка однородности деформационных свойств материала по глубине. Производится вдавливанием кольцевых или сплошных с плоским основанием инденторов различного диаметра, с последующим определением упругих постоянных материала изделия. Изменение (увеличение или уменьшение) получаемых значений модуля упругости при увеличении диаметров инденторов показывает, что деформационные свойства глубинных слоев материала отличаются от поверхностных. Для определения параметров функции неоднородности по глубине следует использовать решения соответствующих контактных задач при переменных по глубине деформационных свойствах материала (прежде всего модуля упругости).
3. Постоянство глубины вдавливания во времени при постоянной нагрузке служит основанием для построения модели материала, ограничиваясь упругими деформациями. В противном случае необходимо строить вязкоупругую модель материала.
4. Используя кольцевой индентор, сцепленный с поверхностью материала, строим обобщенную зависимость интенсивности напряжений от интенсивности деформаций вплоть до отрыва (среза) кольцевого слоя. Таким образом, получаем экспериментальную зависимость, которой можно затем сопоставить обобщенную математическую зависимость интенсивности напряжений от интенсивности деформаций вплоть до разрушения материала. Такие зависимости можно получить для различных значений среднего напряжения, которое может создаваться в поверхностном слое материала с помощью составного индентора [1].

В случае актуальности неразрушающего контактного испытательного воздействия на поверхность изделий более подходящими являются инденторы со сфероидальной или эллипсоидальной формой наконечника. Результатом подобных испытаний будет нелинейная зависимость силы сопротивления от глубины вдавливания, что несколько затрудняет обработку результатов испытаний, но основная методика испытаний сохраняется.

Литература:

1. Галынский Ю. А., Пономарев С. В. Определение упругих постоянных эластичного материала методом локального деформирования. Механика деформируемого твердого тела. — Томск: Изд-во Том. Ун-та, 1968.- с.34–38.
2. Reissner А., Sagoci H. F. Foreed Forsional Oscillatios of an Elastic Half Space. — Journal of applied Phisics, 1994, v.15, p.652–662.
3. Пономарев С. В. А.с.717619 на изобретение «Устройство для определения механических характеристик материалов».