В статье автор проводит исследование понижающих коэффициентов к модулю упругости бетона при квазинелинейном расчете железобетонного балочного перекрытия.
Ключевые слова: понижающий коэффициент, модуль упругости, железобетон, нелинейный расчет, балочное перекрытие.
В данной статье было произведено исследование по анализу понижающего коэффициента модуля упругости балки в зависимости от изменения отношение высот плиты к балке. Расчетная модель представлена на рис. 1.
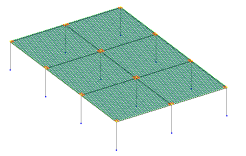
Рис. 1. Расчетная схема
Было выдвинуто предположение, что некорректно предполагать, что для предварительного расчета системы, в которую входят плита и балка, принимать одинаковый понижающий коэффициент модуля упругости в обеих конструкциях. Поэтому для представления более близкой к реальной работы конструкций, кроме расчетов в упругой постановке и квазинелинейной постановке с учетом коэффициентов по СП430 [2], был произведен расчет с учетом нелинейной работы материалов по диаграмме деформирования по СП 63 [1].
Цель расчетов состояла в том, чтобы экспериментально определить изгибную жесткость балки в составе плиты перекрытия в зависимости от соотношения высоты плитной части к высоте балочной части. Кроме этого также проследить зависимость изменения значения, понижающего коэффициент начального модуля упругости при расчете в первом приближении.
В качестве численно-экспериментальной модели принята каркасная система, которая состоит из колонн и балочного перекрытия. Для исследования зависимости были выбраны различные высоты плиты (от 140, 200 и 250 мм) без изменения высоты балки (400 мм). Это было принято, чтобы понять, как влияет отношение плитной части к балочной части на перераспределение усилий в перекрытие. Размер колонн — 400х400 мм, шаг колонн — 6 м. Класс бетона — B25, класс арматуры — А400.
При выполнении физического нелинейного расчета необходимо задать диаграммы деформирования материалов.
На рис. 2 представлены принятые линейно-кусочные диаграммы деформирования для бетона и стали согласно СП 63.13330.2018 [1]. Параметры диаграмм назначаются в зависимости от класса бетона и арматуры и длительности нагружения.
![Линейно-кусочные диаграммы деформирования материалов по СП 63.13330.2018 [1]](https://articles-static-cdn.moluch.org/articles/j/103849/images/103849.002.png)
![Линейно-кусочные диаграммы деформирования материалов по СП 63.13330.2018 [1]](https://articles-static-cdn.moluch.org/articles/j/103849/images/103849.003.png)
Рис. 2. Линейно-кусочные диаграммы деформирования материалов по СП 63.13330.2018 [1]
Таблица 1
Результаты расчета
|
В пролете |
На опоре |
В пролете |
На опоре |
В пролете |
На опоре |
В пролете |
На опоре | |||||||||
|
Расчет в упругой поставке |
Квазинелинейный расчет |
Нелинейный расчет |
Квазинелинейный расчет с уточн. жесткостями балки | |||||||||||||
|
М, кН м |
Площадь арматуры, мм 2 |
М, кН м |
Площадь арматуры, мм 2 |
М, кН м |
Площадь арматуры, мм 2 |
М, кН м |
Площадь арматуры, мм 2 |
М, кН м |
Площадь арматуры, мм 2 |
М, кН м |
Площадь арматуры, мм 2 |
М, кН м |
Площадь арматуры, мм 2 |
М, кН м |
Площадь арматуры, мм 2 | |
|
h пл / h пл =0,35 |
52,3 |
7,04 |
-113,4 |
7,07 |
54,75 |
7,52 |
-107,2 |
6,71 |
60,67 |
9,76 |
-125,2 |
9,52 |
55,3 |
9,01 |
130,2 |
8,96 |
|
10 % |
23 % |
14,4 % |
29,5 % |
9,3 % |
7,6 % |
3,9 % |
5,9 % | |||||||||
|
h пл / h пл =0,5 |
32,6 |
6,48 |
-78,8 |
5,6 |
33,4 |
6,64 |
-73,3 |
5,2 |
42 |
8,48 |
-94,2 |
7,35 |
40,7 |
8,1 |
-93,7 |
7,34 |
|
20,5 % |
21,7 % |
22 % |
29,3 % |
3,1 % |
4,5 % |
0,5 % |
0,2 % | |||||||||
|
h пл / h пл =0,625 |
19,1 |
3,92 |
-51,35 |
4,16 |
19,5 |
4,0 |
-47,5 |
4,4 |
20,3 |
4,64 |
-59,5 |
5,28 |
19,7 |
4,3 |
-60,6 |
5,04 |
|
4 % |
13,8 % |
20,2 % |
16,7 % |
2,9 % |
7,3 % |
1,8 % |
4,5 % | |||||||||
Примечание: 4,8 % — разница между значением, полученным при нелинейном расчете, и значениями, полученными при квазинелинейными расчетами
Подбор жесткостных характеристик производился таким образом, чтобы при квазинелинейном и нелинейном расчетов происходило схождение изгибающих моментов.
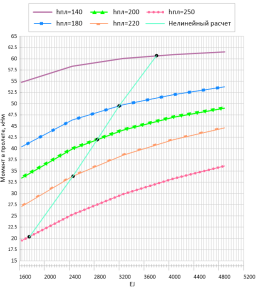
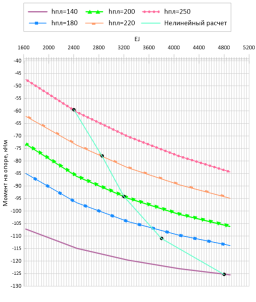
Рис. 3. Зависимость моментов в пролете и на опоре балки (кНм) от жесткости балки
Таким образом, при подборе понижающего коэффициента отдельно, на опоре и в пролете балки, были получены значения изгибающим моментов, разница которых составила: менее 10 % в пролете и менее 4 % на опоре, по сравнению с результатами, полученным в нелинейном расчете. Так же разница в площади арматуры составила менее 10 %, что меньше, по сравнению с результатами, полученными при квазилинейном расчете с понижающими коэффициентами по нормам.
При анализе табл. 1 можно сделать вывод о том, что при уточнение понижающего коэффициента при первом приближении, при этом задавая разные жесткостные характеристики в пролете и на опоре балки, можно получить более точные значения, как и усилий, деформаций, так и требуемую площадь арматурования участков, как получается при расчете в нелинейной постановке.
Что касается влияния отношения балочной и плитной части на значение модуль упругости, принимаемого для расчета, то исследование показало, что чем меньше высота плитной части, тем больше усилий на себя перетягивает балка. По сути, в опорной части балки ничего не изменяется, за счет учета понижающего коэффициента, часть изгибающего момента и переходит в балки, но в суммарной составляющей значения усилий в этой части остаются неизменными, так же, как и требуемое значение суммарной площади арматуры в данной зоне остается постоянной. Но в пролетной части перераспределение усилий более значимое явление, так как происходит перераспределение усилий из растяной зоны плиты в растянутую зону балки, что находится конструктивно гораздо ниже нижней грани плиты. И поэтому количество требуемой арматуры в растянутой части балки увеличивается, а в плитной части наоборот, уменьшается.
Литература:
- СП 63.13330.2018. Бетонные и железобетонные конструкции. Основные положения. СНиП 52–01–2003 (с Изменением № 1)
- СП 430.1325800.2018 Монолитные конструктивные системы. Правила проектирования (с Изменением N 1)

