Гравитационное поле является основой существования множества устойчивых систем, образуемых относительно большой центральной массой и малыми массами, вращающимися вокруг нее. В поле Солнца расположение орбит образует закономерную последовательность, в которой характеристики движения внешних соседних планет (средние расстояния, напряженности, периоды и др.) примерно в 2 раза больше, чем внутренних. Это обстоятельство отражено закономерностью Тициуса-Боде, которая до настоящего времени не имеет удовлетворительного объяснения. Закономерности соответствуют период Галактического года (около 200 миллионов лет) и геологический период (около 80 миллионов лет). Структурно-функциональные изменения живых организмов и биологических сообществ составляют иерархическую последовательность, в которой, кроме палеонтологических и многолетних, существуют колебания с окологодовыми и околополугодовыми, около-14-дневными и около-7-дневными, околосуточными и около-12-часовыми, около-3-часовыми и около-1,5-часовыми и другими периодами [1]. Поскольку закономерность Тициуса-Боде связана с гравитационным полем, то ее проявления в других объектах и процессах могут свидетельствовать об участии в них гравитационных полей.
Установленное Галилеем одинаковое ускорение свободного падения тел разной массы в вакууме, в результате которого они проходят одинаковое расстояние за одинаковое время, показывает, что в поле тяготеющей массы они проявляют себя как «пробные частицы». Поэтому было сделано предположение, что планеты, как «пробные частицы», своим положением и движением отражают строение и динамику пространственно-временных интервалов гравитационного поля Солнца. Интервал напряженностей гравитационного поля связан с центральной массой (М) [2]:
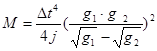
∆ t - интервал времени изменения напряженности g t от g t-1 до g t+1 , соответствующий ∆R на расстоянии R от геометрического центра М, j – гравитационная постоянная. В этом же интервале можно описать геометрические свойства поля с помощью кривизны (К) – как относительного ускорения (а) изменения расстояния в 1 м:
в формулу которой входит удвоенный эксцентриситет (е):
,
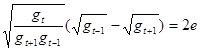связанный с относительным расстоянием между апогелием и перигелием орбиты.
Любая орбита при максимальном эксцентриситете представляет собой эллипс с длинной полуосью - расстоянием апогелия (А) до геометрического центра Солнца, и короткой – расстоянием перигелия (П). Перпендикулярно к полуосям можно выделить горизонтальные плоскости орбиты, проходящие через диаметр Солнца и представляющие собой эллипсы, длинные оси которых лежат в плоскости эклиптики (вертикальной). Тогда большая часть пространства гравитационного поля Солнца для каждой орбиты делится горизонтальными плоскостями на 2 несимметричных полупространства эллипсоида – больший объем стороны апогелия и меньший - стороны перигелия. Если планета своим движением вокруг Солнца отражает изменения гравитационного поля, то в области орбиты за период обращения планеты величины напряженностей в противоположных полупространствах изменяются постепенно и одновременно, начиная со среднего расстояния (е=0) до установления максимальных эксцентриситетов разного знака в А и П, а затем снижаются до среднего радиуса. В одном полупространстве находится планета, а другое свободно. Неравенство всех характеристик полупространств А и П означает поляризацию гравитационного поля Солнца в границах каждой орбиты за полупериод достижения максимального эксцентриситета.
В выражение эксцентриситета орбиты входит множитель 
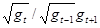, который определяет его величину, обратно зависящую от напряженности. Поэтому величина эксцентриситета в П - полупространстве будет тем больше, чем ближе к среднему R, а в А –полупространстве – чем ближе к его полуоси. Это означает, что максимумы эксцентриситета в А и П полупространствах орбит по отношению к геометрическому центру Солнца не лежат на одной прямой и возникают не одновременно - сначала в П-, а затем в А-полупространстве. Другой множитель 
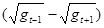определяет скорость изменения напряженности (очевидно, обратную производную) и задает знак эксцентриситета. При возрастании напряженности эксцентриситет не только уменьшается, но и имеет отрицательное значение, а при уменьшении напряженности эксцентриситет возрастает и имеет положительное значение. Эти знаки соответствуют процессу изменения относительных расстояний с относительными ускорениями в полупространствах орбиты. Тогда полупространство апогелия (А-полупространство), имеющее меньшую энергию, будет иметь знак минус «-», а полупространство перигелия (П-полупространство), имеющего большую энергию, будет иметь «+». Параллельно и однонаправленно будет изменяться и квадрат интервала времени:
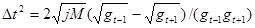
Как е, так и ∆t 2 имеют ход производных, абсолютные величины которых изменяются с периодом примерно в 2 раза меньшим периода орбиты, что практически и соответствует периоду соседней внутренней орбиты. Являясь производной поля переменной напряженности в области орбиты, эксцентриситет будет иметь нулевые значения (е=0) в экстремальных точках орбиты, а максимумы абсолютной величины скорости изменения напряженности (е = ± максимум) могут определять А и П соседней внутренней орбиты.
За полупериод в полупространстве П орбиты возрастание напряженности до максимума обусловит А-полупространство внутренней орбиты, а на противоположной А-стороне орбиты - одновременное уменьшение напряженности - П-полупространство внутренней орбиты. За следующий полупериод на стороне П орбиты напряженность начинает уменьшаться, что определит П-полупространство внутренней орбиты на этой же стороне Солнца и А полупространство – на противоположной стороне. Т.о., на одной стороне Солнца знаки полупространств внешней и внутренней орбит противоположны при возрастании напряженности и совпадают при ее уменьшении. Это создает разные по величине и направлению геометрические изменения в полупространствах, т.е. несимметричные приливные волны, периферические интервалы которых содержат орбиты, отражающие приливное неравенство.
При смене направления изменения напряженностей полупространств орбиты происходит закономерное изменение поляризации ближайшей внутренней орбиты («переворот»). Изменение кривизны происходит по всему объему, поэтому относительно осей должны возникать 2 симметричные орбиты, пересекающиеся в области их средних радиусов. Из таблицы 1 видны отличия эксцентриситетов, интервалов времени и величин кривизны полупериодов пространств апогелия (от А до R, где RA – среднее расстояние между R и A) и перигелия ( от П до R, где RП – среднее расстояние между R и П) орбит планет. В П-полупространстве скорость изменения напряженности реально больше, чем в А-полупространстве, поэтому и геометрические изменения и их скорости также больше (табл.1).
Таблица 1.
Некоторые характеристики полупространств орбит планет.
Марс Земля Венера
е ∆t 106 c К10-14 c-2 е ∆t 106 c К10-14 c-2 е ∆t 106 c К10-14 c-2
А П А
RA -0,0523 4,53 1,018 RП 0,0070 0,82 4,103 RА -0,0028 0,33 10,397
R -0,0932 5,66 1,162 R 0,0167 1,29 3,996 R -0,0067 0,51 10,514
RП -0,0397 3,43 1,345 RА 0,0970 1,00 3,912 RП -0,0040 0,39 10,641
П А П
Если движение планеты отражает изменения эксцентриситета орбиты, то в полупериоде изменения е сначала возникают А и П внутренней орбиты в П-полупространстве вблизи ее средних радиусов R, а затем в А вблизи ее оси. Можно предположить, что траектория движения планеты на внутренней орбите будет проходить примерно как на рис. 1. Сам процесс вращения, очевидно, возможен вследствие «переворота» полярности внутренней орбиты за счет смены направления изменения напряженности орбиты: возрастания на снижение или наоборот. В области 1R и 5R находятся средние радиусы орбиты, к которым близки по времени и расположению средние радиусы внутренней орбиты, а в 3R, 7R –средние радиусы внутренней орбиты, соответствующие е=0 в А и П орбиты. При возрастании кривизны (слева) в П-полупространстве орбиты должны возникнуть максимумы эксцентриситета (2А и 4А), в одном из которых может находиться планета. Максимум 2А предположительно находится вблизи 1R и возникает быстрее, чем 6П и П около оси в А-полупространстве. При уменьшении е после 2А в 3R, 4П, 5R (рис.2в, нанп, дадп, см стр.6) возникает средний радиус внутренней орбиты, затем планета попадает в 6П, а при достижении е=0 - в 7R. После изменения направления возрастания кривизны на уменьшение в 7R период заканчивается в 8А. Однако, реальная картина может быть сложнее, т.к. в плоскости эклиптики как «производные» орбиты, так и орбиты, тоже, в свою очередь, «производные, и т.д., должны быть двойными.
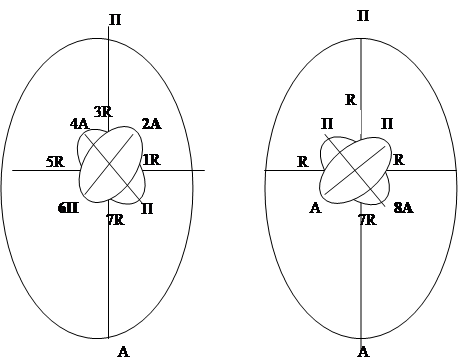
Рис.1
Предполагаемая орбита при возрастании (слева) и уменьшении (справа) абсолютной величины кривизны и соответствующие пары внутренних орбит. Цифрами показана возможная траектория движения планеты по внутренней орбите.
Поскольку в поставленной задаче необходимо выявить предполагаемую связь внешних и внутренних орбит, то необходимы расстояния, даты и гелиоцентрические долготы А и П последовательности планет. Для этого использовали данные Марса, Земли, Венеры и Меркурия из Астрономических ежегодников 1991-1993 г.г.[3,4,5], которые были экстраполированы на каждые сутки. Алгоритм расчетов по датам и интервалам: расстояние – напряженность – эксцентриситет (шаг оценки е составляет 1 сутки, диапазон напряженностей - 9 суток)– квадрат интервала времени – кривизна. В зависимости от направления изменения напряженности на орбите, А и П внутренней орбиты могут находиться либо на А-, либо на П-стороне планеты. Если планета внутренней орбиты находится со стороны положения планеты внешней орбиты, то считаем эту сторону дневной (д), а противоположную – ночной (н). В определенном диапазоне координат (дат) дневную сторону А можно считать ночной стороной П и наоборот. Так, перигелий Марса 18.07.92 имеет долготу 14,56о, тогда его полупространство ограничено горизонтальной плоскостью с двух сторон примерно углами (14,56 о± 90о), которые соответствуют датам 25.07.92 и 1.01.93. Эллиптичность орбит обуславливает неточность в определении координат, т.к. в П-полупространстве дуга окружности уменьшается, а в А-полупространстве увеличивается на угол α, который связан с эксцентриситетом: е = sin α, поэтому углы на стороне П будут меньше 90о, а на стороне А больше.
Для анализа предполагаемой обусловленности знаков полупространств внутренних орбит изменением кривизны полупространств орбит были рассчитаны величины эксцентриситетов по датам. Чтобы показать две стороны орбиты, ход абсолютных значений ее эксцентриситета представлен двойным графиком (с отображением в отрицательной части графика умножением на (-1)). На рис. 2а вверху по датам показаны два апогелия, перигелий и средние радиусы Марса: 1А, R, П, R 2А. Согласно реальным датам и координатам по отношению к А и П- полупространствам Марса, на графиках е отметили положения А и П Земли и в соответствии с ними определили знаки (±). Положение средних радиусов орбиты Земли – это е=0 и примерные даты между ее А и П, которые показаны на кривых
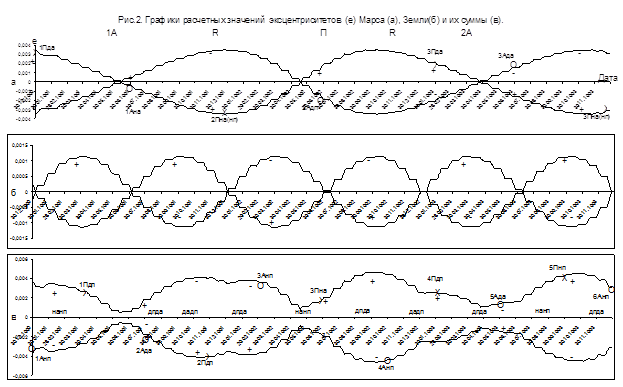
эксцентриситета. В выбранном интервале времени на графике эксцентриситета Марса положение (2Адп) означает второй апогелий (2А) Земли и его дневное (д) расположение по отношению к П (п) Марса. Расположение А и П внутренних орбит на графиках обозначены согласно д и н сторонам орбит: например (рис.2 в), 3Пна – это 3 перигелий Венеры ночной стороны апогелия Земли (2А). Поскольку А и П не лежат на одной прямой с геометрическим центром Солнца, то иногда положению А и П планет внутренних орбит, а чаще их средних радиусов (где, возможно, относительные ускорения компенсируют, друг друга) соответствуют стороны как П, так и А орбит (ночные - нпна) или (дневные - дадп), на рисунке они показаны значками (Х-перигелий и О –апогелий) как нп(на); да(дп) (рис.2в).
На графике видно, что перигелии Земли, кроме 3Пда, находятся примерно в максимумах е орбиты Марса в области средних радиусов его орбиты, но на разных сторонах, а все А расположены около оси времени близко к его А и П. Кроме 1Ана, предположение об ожидаемой обусловленности знаков полупространств орбиты Земли изменением эксцентриситета орбиты Марса находит подтверждение.
Второй график на рис.2(б) – ход эксцентриситета Земли, рассчитанный из ее расстояний на орбите, где знаками (±) отмечена предполагаемая полярность пространства орбиты Венеры. Однако, реальное положение А и П Венеры (рис. 2в) во многих случаях не согласуется с предполагаемыми знаками (сторонами) хода эксцентриситета Земли. Согласно периодам е Марса, знаки объединяют примерно по два последовательных периода, а положения А и П Венеры согласуются со знаками е Марса, кроме 5Пнп. После суммирования абсолютных величин эксцентриситетов Марса и Земли положение и знаки экстремальных точек Венеры были показаны на графике (рис.2в).
Это значит, что в создании орбит планет суммарно участвуют эксцентриситеты не только ближайших, но и других орбит поля Солнца.
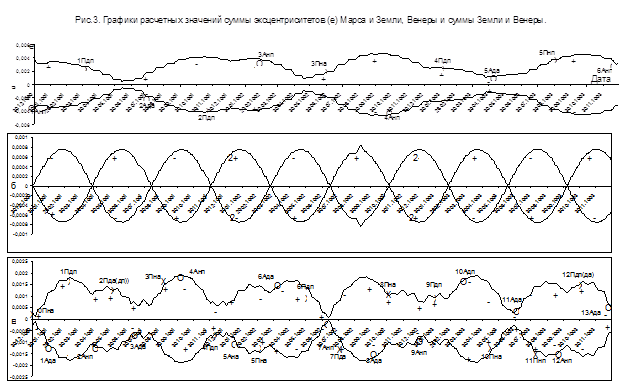
На рис.3а показана динамика суммы эксцентриситетов орбиты Марса и Земли для орбиты Венеры (как на рис. 2в). На рис. 3б - график эксцентриситета Венеры, рассчитанного из ее расстояний от Солнца. Количество полученных колебаний эксцентриситета меньше, чем количество реальных орбит Меркурия за это же время. Если рассчитать е Меркурия из е Земли (а не из орбиты Венеры), то эти количества совпадают. Знаками показана предполагаемая полярность, где с 30.11.91 по 30.03.92 и с 30.10.92 по 28.02.93 показаны (2+ и 2-), т.к. в эти интервалы времени предположительно должны находиться по 2 орбиты с одинаковыми полярностями ( как на рис.2б). Возможно, эти противоречия связаны с усреднением параметров орбиты планет при расчете их расстояний от Солнца. На рис. 3в - показан ход суммы абсолютных значений эксцентриситетов Венеры и Земли, на графике которой показаны положения А и П Меркурия. Здесь также очевидно влияние суммы эксцентриситетов орбит Марса и Земли на положения А и П Меркурия и закономерную смену знаков по сторонам Солнца в области их орбит. Таким образом, орбиты Венеры и Меркурия с периодами, близкими к эксцентриситету Марса, группируются и чередуются относительно соседних внешних орбит преимущественно либо А-, либо П-сторонами.
Расчетные значения эксцентриситетов и интервалов времени ∆t максимальны у орбиты Марса, меньше у Земли и еще меньше у Венеры. Однако, эксцентриситеты показывают направления и величины изменений расстояний, которые являются результатом относительных ускорений (а) изменения средних радиусов орбит (∆R), обусловленных кривизной: K = 4е /∆t2
Величины кривизны, наоборот минимальны у Марса, а максимальны у Венеры, поэтому в колебаниях суммы относительных ускорений будут лучше всего выражены высокочастотные составляющие. В таблице 2 показаны связи орбит с собственными значениями кривизны. Однако, в них не выражены знаки и периоды абсолютных значений е, с которыми могут быть связаны внутренние соседние орбиты, поэтому для анализа и был использован ход эксцентриситетов.
Таблица 2.
Экстремальные и средние величины кривизны (К10-14с-2) орбит
и коэффициенты их корреляции (к/к) с расстоянием от Солнца.
Орбита К макс К мин К сред. к/к
Марс 1,51 0,86 1,08 -0,99
Земля 4,18 3,78 3,98 -0,99
Венера 10,71 10,29 10,50 -0,99
Меркурий 134,10 39,29 72,68 -0,98
Если относительные расстояния, связанные с изменением среднего радиуса, «производных» внутренних орбиты обусловлены динамикой эксцентриситета, то они
Таблица 3.
Корреляции расстояний АП орбиты Земли и абсолютных значений эксцентриситета Марса; расстояний АП орбиты Венеры и суммы абсолютных значений эксцентриситета Земли и Марса в 1991-1993 г.г.
орбиты Земли к/к орбиты Венеры к/к
1Пда – 1Ана -0,99 1Анп – 1 Пдп -0,78
1Ана – 2Пнпна -0,97 1Пдп - 2Ада 0,12*
2Пнпна – 2Ада - 0,90 2Ада - 2Пдп 0,93
2Ада – 3Пда -0,31* 2Пдп - 3Анп 0,32*
3Пда – 3Ада -0,62 3Анп - 3Пна -0,54
3Ада – 4Пнанп -0,82 3Пна - 4Анп -0,88
4Анп - 4Пдп -0,93
4Пдп- 5Ада 0,79
5Ада – 5Пнп 0,99
5Пнп – 6Анп 0,92
должны коррелировать. Коэффициенты корреляции (к/к) одновременных среднесуточных расстояний АП (ПА) внутренних орбит с динамикой эксцентриситетов орбит представлены в таблицах 3 и 4. Знаки к/к здесь не существенны, они зависят от расположения А и П и хода эксцентриситета относительно оси времени. Достоверные (P<0,01) корреляции подтверждают возможность участия эксцентриситетов орбит в формировании положения и динамики внутренних соседних орбит.
Таблица 4.
Корреляции расстояний А – П орбит Меркурия и суммы абсолютных
значений эксцентриситетов Земли и Венеры в 1991-1993 г.г.
орбиты Меркурия к/к орбиты Меркурия к/к
0Пна – 1Ада 0,94 7Анп – 7Пдп -0,97
1Ада – 1Пдп -0,81 7Пдп – 8Ада -0,27*
1Пдп – 2Адп -0,95 8Ада– 8Пна 0,75
2Адп – 2Пдпда 0,50 8Пна – 9Анп -0,89
2Пдпда – 3Ада -0,79 9Анп – 9Пдп -0,19*
3Ада – 3Пна -0,97 9Пдп – 10Адп 0,99
3Пна – 4Анп 0,64 10Адп – 10Пна 0,93
4Анп - 4Пдп 0,98 10Пна – 11Ада -0,97
4Пдп– 5Ана 0,71 11Ада- 11Пнп - 0,96
5Ана – 5Пна -0,68 11Пна – 12Анп -0,59
5Пна – 6Ада 0,55 12Анп - 12Пдп -0,95
6Ада – 6Пдп 0,87 12Пдпда – 13 -0,87
6Пдп – 7Анп -0,98
*Р>0,05
Из вышеизложенного следует, что эксцентриситет и квадрат интервала времени изменяются практически как производные напряженности и задают знак полупространства внутренней орбиты. Поэтому расположение экстремальных величин эксцентриситетов внутренних соседних орбит по отношению к орбитам должно иметь сходство с положениями экстремумов производных относительно их периодических функций. Несмотря на незначительные изменения координат А и П орбит в последовательных уменьшающихся периодах, очевидно их спиральное расположение вокруг Солнца (табл.5).
Таблица 5.
Значения гелиоцентрических долгот П и А орбит Марса, Земли, Венеры и Меркурия.
Орбиты Дата По Дата Ао
Марса 18.07.92 14,6 23.04.93 154,7
Земли 3.01.92 102,0 3.07.92 281,4
Венеры 17.07.92 137,0 4.11.92 313,1
Меркурия 4.03.92 66,1 18.04.92 235,2
Поскольку А и П орбит заняты планетами поочередно, то симметрия полупространств относительно осей обуславливает существование в пространстве спирального вращения энергии гравитационного поля вокруг Солнца. Вследствие суммирования относительных ускорений разных периодов и знаков, спиральность должна быть изменчивой и более сложной. Это дает основание считать, что гравитационное поле – это градиент потенциала, который последовательно и спирально усиливается и ускоряется от периферии к центральной массе, представляя вихревое движение энергии.
Неоднородное в пространстве поле центральной массы при изменении во времени создает геометрические (приливные) изменения силовых линий и эквипотенциальных поверхностей, обуславливая переменную поляризацию определенных интервалов гравитационного поля. Колебания энергии гравитационного поля делает интервалы орбит взаимно обуславливающими друг друга по направлению от периферии поля Солнца к его центру, представляя единую систему, в которой по периодам выделяются разные геометрические изменения (R ± ∆ R). Связанный с центральной массой градиент энергии при ее постепенном и непрерывном колебательном изменении происходит по всему объему гравитационного поля, поэтому геометрические изменения должны обуславливаться периодическими изменениями суммарных относительных (приливных) ускорений в любой его точке. Интервалы расстояний орбит планет выделяются тем, что периоды их изменения связаны с центральной массой Солнца, а на других расстояниях они соотносятся с фиктивными массами. Зависимость от расстояния (диаметра орбиты) показывает, что относительные ускорения (а) приливной волны любого периода усиливаются с возрастанием расстояния от центральной массы и должны иметь место на любых орбитах:
a = КR= ± 4еR/∆ t2 = ± 4 ∆R/∆ t2,
Массы планет не имеют отношения к возникновению этого каскада последовательных, обуславливающих друг друга приливных волн, а лишь отражают своим движением сложнопериодическое поле Солнца. По-видимому, энергия гравитационного поля существует как система закономерно обусловленных приливных волн иерархической последовательности периодов, которые на определенных расстояниях в интервалах их геометрических изменений относительно массы Солнца могут быть заселены планетами. Поэтому такие волны должны иметь место и за пределами заселенной планетами части солнечной системы. Тогда закономерность возникновения более короткопериодных приливных волн будет реализовываться в направлении к Солнцу. Внутри Солнца и на его поверхности это может отражаться сложнопериодическими геометрическими изменениями: вращательными, поступательными разного направления и спиральными движениями областей его подвижной массы и изменениями ее локальных плотностей. Амплитуды и периоды этих движений должны отражать суммарные приливные ускорения, влияющие на его активность, и одновременно и непрерывно изменяться по всему спектру составляющих сложного колебания. Такую природу может иметь и 11-летний цикл его активности (по-видимому, периода орбиты Юпитера, примерно 12 лет), который в определенные годы может суммироваться в последовательных циклах, давая усредненную около-25-летнюю периодичность. При этом амплитуды и периоды этого цикла будут изменяться по более долгопериодным колебаниям, обуславливая разную его активность в соответствии с ними. В активности Солнца должны присутствовать периоды, соответствующие не только обращению планет, но и незаселенных приливных волн, начиная, как минимум, с Галактического года. Можно ожидать, что периоды обращения и расстояния планет от Солнца будут также меняться в зависимости от всех составляющих сложнопериодического колебания кривизны, что скажется на динамике внутри масс планет и условий на них. Следствием долгопериодных изменений направления напряженности, независимо от ее величины, могут быть хорошо известные геологические, климатические и палеонтологические «перевороты» условий в Солнечной системе, которые охватывают всю иерархическую лестницу периодических изменений условий и на Земле. Предложенная гипотеза, возможно, позволит оптимизировать прогнозы природных процессов и явлений на Земле в их долгопериодной и короткопериодной динамике.
Литература
- Биологические ритмы. В двух томах. Т.2. /Пер. с англ. Под ред. Ю. Ашоффа/, М.: Мир,1984, 262 с.
- Бортникова Г.И. К механизму взаимодействия гравитации и массы// Журнал Молодой ученый, 2009, № 3, с. 5-9.
- Астрономический ежегодник СССР на 1991 г., т 70 /Л.,ЛО: Наука, 1989, 693 с.
4. Астрономический ежегодник СССР на 1992 г., т 71 / Л.,ЛО: Наука, 1990, 691 с.
5. Астрономический ежегодник СССР на 1993 г., т 72 / Л.,ЛО: Наука, 1991, 691 с.
