Во многих процессах различных наук (медицина, физика, биология, физиология питания и др.) построение моделей по статистическим данным представляет серьезный интерес. В рамках данной статьи интерес представляет построение моделей дискретно-непрерывных процессов.
Проблема идентификации или моделирования – одна из актуальных в кибернетике не сегодняшний день. Формулировка задачи идентификации весьма разнообразна и зависит от априорной информации [1].
Задача идентификации разделена на две задачи: задача идентификации в «узком» смысле и задача идентификации в «широком» смысле. Идентификация в «широком» смысле отличается тем, что априорной информации меньше и она более расплывчата. Наиболее развита идентификация в «узком» смысле [1].
Процесс идентификации складывается из двух взаимосвязанных этапов: идентификации структуры модели и идентификации параметров в моделях выбранной структуры. При построении структуры модели используется априорная информация об объекте. Для каждого класса объектов формируются банки структур с сопутствующей информацией [1].
Существуют 3 уровня априорной информации о предполагаемом процессе:
- Байесов уровень, при котором информация об объекте может быть как полной (максимально возможной), когда точно заданы модель объекта, статистические характеристики наблюдений и возможных помех, так и неполной, когда вероятностные характеристики наблюдений, помех и вид модели известны с точностью до набора параметров;
- уровень параметрической неопределенности, при котором неизвестны законы распределения измерений и помех, а структура модели задана с точностью до набора параметров. Присутствуют выборки статистически независимых наблюдений переменных объекта;
- уровень непараметрической неопределенности когда неизвестны ни законы распределения помех и измерений, ни структура модели. Известны некоторые качественные характеристики объекта: например, объект статический или динамический, однозначны или нет связи между его переменными и т.п. Имеются выборки статистически независимых наблюдений переменных объекта.
На практике часто мы имеем следующий уровень априорной информации об объекте: неизвестна параметризованная структура модели объекта, но известны некоторые качественные свойства объекта. В таком случае целесообразно использовать методы непараметрической теории идентификации (в широком смысле), которые являются более универсальными, т.к. используют только исходную статистическую выборку входных и выходных значений и некоторые описательные характеристики объектов (статический или динамический объект и т.д.) [5]
Рассмотрим задачу идентификации дискретно-непрерывных процессов к которым можем отнести следующий процесс (рис. 1). Процесс относится к классу дискретно-непрерывных, так как сам процесс непрерывен, но данные фиксируются в дискретные промежутки времени.

Рисунок 1. Схема процесса в теории моделирования и идентификации
Где: 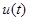 - вектор входных управляемых переменных,
- вектор входных управляемых переменных, 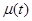 - вектор входных неуправляемых переменных,
- вектор входных неуправляемых переменных, 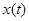 - вектор выходных переменных,
- вектор выходных переменных, 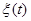 - случайные возмущения, действующие на объект с нулевым математическим ожиданием и ограниченной дисперсией. К этому классу значений можно отнести физические возможности и недостатки экспериментатора, погрешности оборудования и др.,
- случайные возмущения, действующие на объект с нулевым математическим ожиданием и ограниченной дисперсией. К этому классу значений можно отнести физические возможности и недостатки экспериментатора, погрешности оборудования и др., 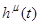 ,
, 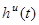 ,
, 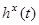 - случайные помехи измерений соответствующих переменных процесса с нулевым математическим ожиданием и ограниченной дисперсией,
- случайные помехи измерений соответствующих переменных процесса с нулевым математическим ожиданием и ограниченной дисперсией, 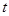 - непрерывное время,
- непрерывное время, 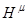 ,
, 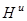 ,
, 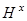 - каналы связи, соответствующие различным переменным, включающие в себя средства контроля, приборы для измерения наблюдаемых переменных,
- каналы связи, соответствующие различным переменным, включающие в себя средства контроля, приборы для измерения наблюдаемых переменных, 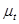 ,
, 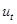 ,
, 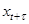 - измерения переменных процесса через интервал времени
- измерения переменных процесса через интервал времени 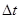 ,
, 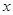 - контролируется через существенно больший интервал времени
- контролируется через существенно больший интервал времени 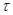 , [3]
, [3]
Рассматривая данный процесс с точки зрения априорной информации Байесова уровня, получаем:
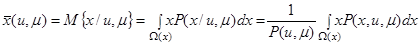
Так как ведется моделирование случайного процесса, то в работе был принят нормальный закон распределения двумерной случайной величины:
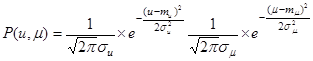
Подставляя формулу распределение в первоначальное выражение, получаем:
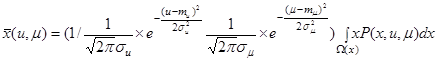
Таким образом, мы смоделировали описываемый выше процесс. Однако, при отсутствии некоторой априорной информации может быть применен другой способ моделирования.
Уравнение идентификации в «узком» смысле будет иметь вид:
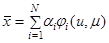
Где: 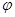 - система линейно-независимых функций,
- система линейно-независимых функций, 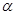 -коэффициент.
-коэффициент.
Данное уравнение возможно использовать применяя метод наименьших квадратов (МНК).
Особым режимом идентификации параметров моделей является адаптивный режим. При этом непрерывно по мере поступления измерений входов и выходов объекта перестраиваются параметры, используется рекуррентный алгоритм.
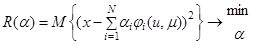
Дифференцируя уравнение критерия по 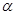 получаем:
получаем:
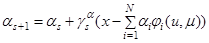 где
где 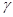 - некий произвольно выбираемый коэффициент.
- некий произвольно выбираемый коэффициент.
Таким образом, с появлением новых данных выборки, имеется возможность дополнять модель, делая ее более точной и адекватной изучаемому процессу.
В общем виде метод наименьших квадратов может быть описан следующим образом. Дана выборка {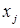 ,
,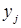 } j = 1,…S. Она представляет пары (
} j = 1,…S. Она представляет пары (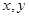 ) одновременно измеренных в количественной шкале значений исследуемых величин. Зависимость y от x будем искать в виде разложения в ряд
) одновременно измеренных в количественной шкале значений исследуемых величин. Зависимость y от x будем искать в виде разложения в ряд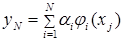 . Где:
. Где: 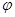 - система линейно-независимых функций.
- система линейно-независимых функций. 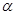 -коэффициент. Необходимо выяснить, существует ли связь между х и у, и исследовать эту связь.
-коэффициент. Необходимо выяснить, существует ли связь между х и у, и исследовать эту связь.
Введем квадратичный критерий:
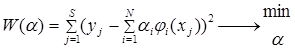
Для отыскания наилучших значений параметров или коэффициентов 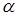 продифференцируем W(
продифференцируем W(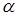 ) по
) по 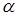 , при N=3 получаем систему линейных уравнений относительно
, при N=3 получаем систему линейных уравнений относительно 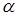 :
:
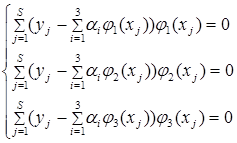
Решаем ее относительно 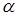 , при наличии выборки в общем виде:
, при наличии выборки в общем виде:
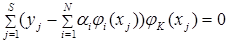 при К=1,2,…N
при К=1,2,…N
В качестве приближения неизвестной функции у=f(x), на основании априорной информации предлагается параметрическая структура вида 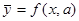 .
.
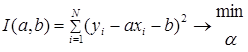
Обозначим класс аппроксимирующих функций через 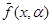 , где a - неизвестный вектор коэффициентов, а меру уклонения определим как выпуклую функцию разности (f(x)-
, где a - неизвестный вектор коэффициентов, а меру уклонения определим как выпуклую функцию разности (f(x)-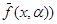 , т.е.
, т.е. 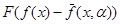 =
=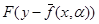 . Поскольку показанные вектора случайны, то и мера уклонения случайна. Поэтому в качестве меры уклонения естественно принять критерий
. Поскольку показанные вектора случайны, то и мера уклонения случайна. Поэтому в качестве меры уклонения естественно принять критерий
R(a) = M{F(y-f(х, a))}.
Задача отыскания наилучшего 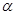 сводится к минимизации
сводится к минимизации 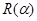 по
по 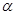 .
.
В работе представлены 2 вида моделей, относящихся к уровню параметрической неопределенности априорной информации. Это следует из того, что, во-первых, оба моделируемых процесса (накопление токсинов как продуктов деятельности патогенных микроорганизмов при хранении продукта и накопление канцерогенных веществ в жире при длительном нагревании) имеют статистические экспериментальные данные. Во-вторых, анализируя эти данные, представляется возможным предположить структуру их модели. Параметры моделей находятся, используя МНК и аппроксимируя имеющиеся статистические данные. Оба процесса касаются производства продукции питания.
Первый процесс связан с накоплением вредных токсичных веществ в продукте питания в связи с размножением в продукте патогенных микроорганизмов. Соответственно, количество токсичных веществ пропорционально количеству патогенных микроорганизмов в продукте. А количество патогенных микроорганизмов, в свою очередь, пропорционально времени хранения продукта или его ингредиентов в условиях, благоприятных для размножения патогенных микроорганизмов (температура выше +5 градусов). В данной работе процесс размножения патогенных микроорганизмов был смоделирован на практическом примере размножения бактерий E. Coli, S. Aureus и Salmonella на питательной среде (мясной фарш) в условиях комнатной температуры и влажности. Замеры производились через каждые 3 часа после момента обсеменения питательной среды в течении 24 часов. Данные заносились в соответствующую таблицу.
Аппроксимация данных процесса накопления вредных веществ в результате деятельности патогенных организмов. После решения соответствующей системы из двух уравнений методом МНК, получаем значения а и b: 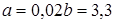
Зависимость y от x имеет вид: 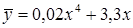
Подставляя в полученную формулу х, находим оценку 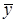 :
:
|
№п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Х |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
|
11,52 |
45,72 |
160,92 |
454,32 |
1062 |
2158,9 |
3958,9 |
6714,7 |
Для наглядности построим экспериментальный график и наложим на него график, полученный в результате аппроксимации экспериментальных данных по МНК (рис. 2):
Аппроксимация процесса накопления вредных веществ в результате увеличения количества канцерогенов при длительном нагреве масла [6]. Примем зависимость y от x в несколько видов, используя кусочную аппроксимацию графика накопления вредных веществ в продукте питания ПБО при жарке:
1.) Примем зависимость y от x в виде 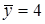 . при
. при 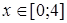
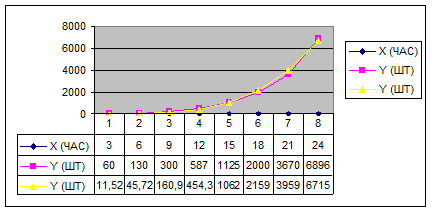
Рисунок 2. График накопления вредных веществ в результате деятельности патогенных микроорганизмов
Где: Х – время (час)
Y (верхний) – количество бактерий (шт), экспериментальные данные
Y (нижний) – аппроксимированные значения
2.) Примем зависимость y от x в виде 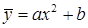 . при
. при 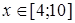
|
№ п/п |
1 |
2 |
3 |
4 |
|
Х |
4 |
6 |
8 |
10 |
|
У |
4 |
4,5 |
7 |
12,5 |
После решения соответствующей системы уравнений методом МНК, получаем значения: а = 0,128, b = - 0,352.
Зависимость y от x имеет вид: 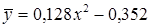
Подставим в найденное уравнение х и найдем 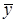 :
:
|
№ п/п |
1 |
2 |
3 |
4 |
|
Х |
4 |
6 |
8 |
10 |
|
|
1,7 |
4,26 |
7,8 |
12,45 |
3.)Логически анализируя третий сегмент экспериментального графика примем зависимость y от x в виде: 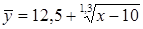
Подставим в найденное уравнение х и найдем 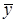 :
:
|
№ п/п |
1 |
2 |
3 |
4 |
|
Х |
10 |
12 |
14 |
16 |
|
|
12,5 |
14,2 |
15,4 |
16,5 |
Для наглядности построим экспериментальный график и наложим на него график, полученный в результате аппроксимации экспериментальных данных по МНК (рис. 3):
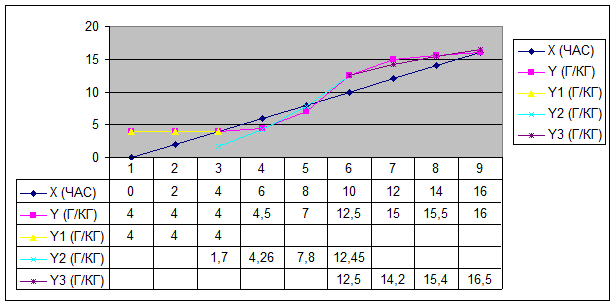
Рисунок 3. График накопления вредных веществ как следствие накопления канцерогенов в технологической среде (масле) при длительном нагреве
Где: X – время нагрева (часы)
Y – экспериментальное количество канцерогенов
Y1 – аппроксимация первой части экспериментального графика
Y2 – аппроксимация второй части экспериментального графика
Y3 – аппроксимация третьей части экспериментального графика
Данные модели призваны показать наглядность накопления вредных для человеческого организма веществ, в процессе приготовления пищи, в частности продукции предприятий быстрого обслуживания. Ставится цель повлиять на уточнение имеющихся в РФ норм СЭС по контролю за качеством продукции питания, с помощью разработки соответствующих рекомендаций. То есть, ввести дополнительные контролирующие этапы в процесс приготовления, обязать ответственных лиц протоколировать все необходимые для проверки опасные и ключевые моменты технологии приготовления и контроля качества поступающей на предприятие ПБО продукции и ее использования. Это позволит строже контролировать качество выпускаемой продукции, а в случае возникновения претензий со стороны потребителя, отследить ответственного за допущенную ошибку.
Литература
1. Медведев, А.В. Анализ данных в задаче идентификации // Компьютерный анализ данных и моделирование: Сборник научных статей Международной конференции. Том 2. Минск, 1995. С. 201-206.
2. Медведев, А.В. Элементы теории непараметрических систем управления // Актуальные проблемы информатики, прикладной математики и механики. Часть 3. Информатика. Новосибирск-Красноярк: Изд-во СО РАН, 1996, 87-112.
3. Гутшмидт, В.А. Непараметрическое моделирование стохастических систем // В.А. Гутшмидт, Я.И. Демченко, М.В. Кураченко, Е.С. Терентьева, А.В. Фаустов. Теория вероятностей, случайные процессы, математическая статистика и приложения. Сборник научных статей Международной научной конференции. Минск, 2008. С. 66-73.
4. Катковник В.Я Непараметрическая идентификация и сглаживание данных / В.Я. Катковник М.: Наука, 1985. 427с.
5. Demchenko Ya. I., Medvedev A.V. Some non-parametric estimation in identification problems for stochastic systems/Ya. I. Demchenko, A.V. Medvedev// Probability theory, random processes, mathematical statistics and applications. Proceedings of the International Scientific Conference. Minsk, 2010. P.
6. Изучение окисления растительных масел при высокотемпературном нагреве во фритюре и разработка способов повышения их стабильности. Автореферат на соискание уч. степени канд. тех. Наук Журавлевой Людмилы Николаевны. Специальность 05.18.06 – Технология жиров, эфирных масел и парфюмерно-косметических продуктов. Санкт-Петербург – 2009.

