К вопросу о классификации пространств с нечеткими мерами

При решении многих задач анализа сложных систем в условиях неопределенности широко используются методы теории вероятностей и математической статистики. Эти методы предполагают вероятностную интерпретацию обрабатываемых данных и полученных статистических выводов. В последнее время возрастает потребность в новых подходах к математическому описанию информации, характеризующейся высоким уровнем неопределенности. Один из возможных подходов может основываться на обобщении понятия меры и построении нечетких мер, свободных от ряда ограничений вероятностной меры.

Существуют различные интерпретации понятия вероятности: классическая частотная интерпретация Лапласа, субъективная вероятность по Байесу и т.д. Наиболее содержательной с математической точки зрения является аксиоматическая трактовка вероятности А.Н.Колмогорова с помощью теории меры.

Мерой называется функция множества m:ρ(X) → R, удовлетворяющая следующим аксиомам:

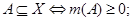1.                                                                                                       (1)

2. m(Æ) = 0;                                                                                                                       (2)

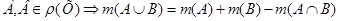3..                                                  (3)

Здесь ρ(X) - множество всех подмножеств Х, а R - множество действительных чисел. При R=[0,1] эти аксиомы определяют вероятностную меру.

Под субъективной вероятностной мерой понимается степень уверенности в данном событии, возникающая у человека на основе известных ему данных. Она всегда зависит от индивидуального опыта и поэтому различна для разных людей. Неясность суждений, основанных на субъективном анализе, обусловливает многие трудности, которые возникают при использовании субъективной вероятности.

Субъективную вероятность можно рассматривать как индивидуальный способ обработки тех аспектов субъективных данных, которые доступны индивидуальному суждению. Однако чаще всего такие суждения неаддитивны. Реальное поведение человека, как правило, противоречит предположению об аддитивности мер, которые он использует при оценке событий. В отличие от субъективной вероятности, нечеткая мера свободна от весьма ограничивающего требования аддитивности, что делает ее особенно привлекательной для решения ряда задач при наличии неопределенности типа нечеткости.

Впервые нечеткие меры применялись для оценки сходства одномерных образов. Например, рассматривалось решение задачи оценки домов. При этом дома оценивались по следующим пяти показателям: площадь, удобства и обстановка, окружающая среда, стоимость, время, требуемое на дорогу до места работы. Известны применения нечетких мер для оценки привлекательности экскурсионных районов, которые оценивались по таким показателям, как красота природы, архитектурные памятники и т.п. Результаты оценок использовались для прогнозирования числа экскурсий в ближайшие десять лет.

В настоящее время существует тенденция вероятностной трактовки нечетких множеств. Следует отметить, что, с точки зрения теории меры, такой подход видится неоправданным, поскольку понятие вероятностной меры является сужением понятия нечеткой меры. Для сравнения рассмотрим обе теоретико-мерные трактовки вероятности и нечеткости.

Пусть (X, φ, ρ) - вероятностное пространство. Здесь φ - минимальная σ-алгебра, содержащая все открытые подмножества множества X, а ρ - вероятностная мера, т.е. Функция множества ρ: φ→[0,1], удовлетворяющая аксиомам (1)—(3). С другой стороны, нечеткое множество описывается функцией принадлежности μ, принимающей свои значения в интервале [0,1]. С точки зрения теории отображений ρ: φ→[0,1] и μ: X→[0,1] -  совершенно разные объекты. Вероятность p определяется в σ-алгебре φ и является функцией множества, а μ(x) есть обычная функция, областью определения которой является множество X. Поэтому понятия вероятности и нечеткого множества не имеет смысла сравнивать на одном уровне абстрагирования.

Функция g, определяемая в виде g: φ→[0,1] называется нечеткой мерой, если она удовлетворяет следующим условиям:

1. g (Æ) = 0;                                                                                                                         (4)                                   

2. g (X) = 1;                                                                                                                          (5)

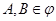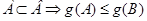3. и ;                                                                                   (6)

4.{F_n}- монотонная последовательность 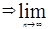g(F_n) = g(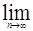F_n).                               (7)

По аналогии с вероятностным пространством общее определение нечеткой меры позволяет определить математическую структуру, соответствующую пространству с нечеткой мерой.

Тройка (X, φ, g)  называется пространством с нечеткой мерой. Для нечеткой меры в общем случае не должно выполняться условие аддитивности: g(AÈB)≠g(A)+g)B). Таким образом, нечеткая мера является однопараметрическим расширением вероятностной меры [3].

Мерой доверия называется такая нечеткая мера g^*, для которой вместо аксиомы (7) используется более сильная аксиома:

  

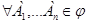
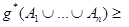
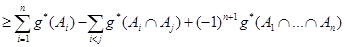                                                  .     (8)

Меру доверия иногда называют также нижней вероятностью и обозначают через b(A).

Пространством с мерой доверия называется математическая структура (X, φ, g^*), функция нечеткой меры g^*  которой удовлетворяет аксиомам (4), (5), (6), (8).

Мерой правдоподобия называется такая нечеткая мера g_*, для которой вместо аксиомы (7) используется более сильная аксиома:

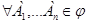
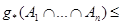
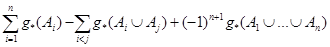 .     (9)

Меру правдоподобия иногда называют также верхней вероятностью и обозначают через pl(A).

Пространством с мерой правдоподобия называется математическая структура (X, φ, g_*), функция нечеткой меры g_*  которой удовлетворяет условиям (4), (5), (6), (9) [2].

Пусть μ и υ - две меры – такие, что 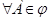 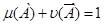 . В этом случае  μ является функцией доверия тогда и только тогда, когда υ-мера правдоподобия [3].

Наибольшее применение при построении нечетких моделей находят меры необходимости, возможности и вероятности.

Мерой необходимости называется такая нечеткая мера g₀, для которой вместо аксиомы (7) используется более сильная аксиома:

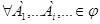
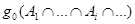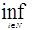  =g₀(A_i).                                                          (10)

Меру необходимости иногда называют согласованной мерой доверия.

Пространством с мерой необходимости называется математическая структура (X, φ, g₀), функция нечеткой меры g₀  которой удовлетворяет условиям (4), (5), )6), (10).

Мерой возможности называется такая нечеткая мера g⁰, для которой вместо аксиомы (7) используется более сильная аксиома:

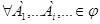
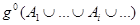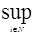 = g⁰(A_i).                                                        (11)

Пространством с мерой возможности называется математическая структура (X, φ, g⁰), функция нечеткой меры g⁰которой удовлетворяет условиям (4), (5), (6), (11) [2].

Пусть μ и υ - две меры - такие, что 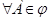 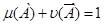 . В этом случае  μ является

согласованной функцией доверия тогда и только тогда, когда υ является мерой возможности [3].

Мера возможности в некотором контексте отражает физические или иные огра-
ничения на значения, которые может принимать та или иная переменная. Так,
например, если рассмотреть число пассажиров, которые могут поместиться в
обычном легковом автомобиле, то с каждым натуральным числом n можно связать число из интервала [0,1], которое содержательно будет соответствовать возможности размещения n пассажиров (не считая водителя) в салоне обычного легкового автомобиля.  Если обозначить эту функцию через g(x), то очевидно, g(l) = 1, g(2) = 1, g(3) = 1, g(4) = 1, g(5) = 0.9, g(6) = 0.5, g(7) = 0.2, g(8) = g(9) =...= 0. Заметим, что оценка возможности - процедура субъективная.

Вероятностной мерой называется такая нечеткая мера р, для которой вместо аксиомы (7) используется более сильная аксиома:

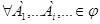
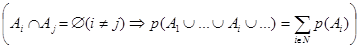 .                       (12)

Пространством с вероятностной  мерой или вероятностным пространством называется математическая структура (X, φ, p), функция нечеткой меры p которой удовлетворяет условиям (4), (5), (6), (12).

Вероятностное пространство обладает наиболее сильной аксиоматикой, обу­словленной необходимостью выполнения условия счетной аддитивности (12).

В завершение рассмотрения нечетких мер приведем их параметрическое пред­ставление, которое не­обходимо для общей систематизации пространств с нечеткой мерой.

 λ-нечеткой мерой называется такая нечеткая мера g_λ, для которой вместо аксиомы (7) используется более сильная аксиома:

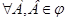
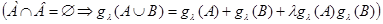                           (13)

Пространством с λ-нечеткой мерой называется математическая структура (X, φ, g_λ), функция нечеткой меры g_λ  которой удовлетворяет условиям (4), (5), (6), (13).

Пространство с λ-нечеткой мерой (X, φ, g_λ) в свою очередь допускает несколько конкретизации в зависимости от значения параметра λ. Наиболее важными с точки зрения классификации пространств с нечеткой мерой являются случаи 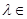(-1;0), λ=1 и 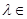(0;+оо), для которых получаются конкретизации введенных в рассмотрение пространств с нечеткой мерой.

Пространством с λ-нечеткой мерой доверия называется математическая структу­ра (X, φ,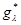), функция нечеткой меры  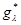которой удовлетворяет условиям (4), (5), (6) и дополнительному условию (13) при  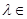(0,+оо).

Пространством с λ-нечеткой мерой правдоподобия называется математическая структура (X, φ, g_*λ), функция нечеткой меры g_*λ которой удовлетворяет усло­виям (4), (5), (6) и дополнительному условию (13) при 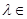 (-1, 0).

Следует заметить, что вероятностное пространство (X, φ, p) является также про­странством с λ-нечеткой мерой при λ=0 [2].

Рассмотренные выше пространства с различными вариантами нечетких мер представляют собой математические структуры, каждую из которых можно счи­тать некоторым абстрактным классом. Важной особенностью подобной точки зрения является определенная взаимосвязь классов пространств с неопределен­ностью, основанная на их конкретизации посредством усиления соответствую­щих аксиом [1].

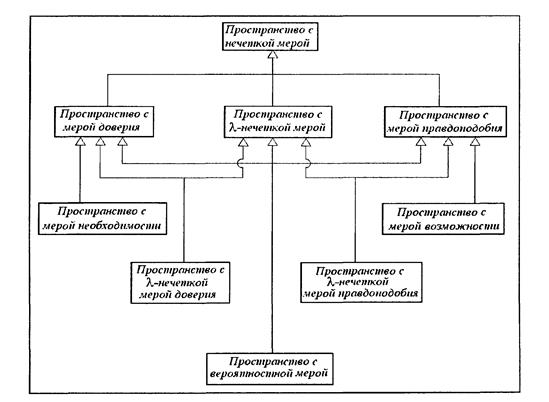
Рис. 1. Диаграмма классов математических структур пространств

с нечеткой мерой в нотации языка UML

 

Таким образом, может быть получена классификация различных классов про­странств с нечеткой мерой, которая представлена на рис.1 в форме диаграммы классов языка UML. На этой диаграмме базовая математическая структура про­странства с нечеткой мерой может использоваться в качестве своеобразного шаб­лона, параметрами которого являются аксиомы рассмотренных нечетких мер. При этом отношение обобщения соответствует усилению отдельных аксиом.

Если между двумя математическими структурами пространств с нечеткой мерой имеется отношение обобщения, то математическая структура нижнего уровня является конкретизацией соответствующей математической структуры верхнего уровня. При этом все математические структуры нижних уровней наследуют ак­сиоматику соответствующих математических структур верхних уровней.

Так, например, математическая структура пространства с мерой необходимости является конкретизацией или частным случаем математической структуры про­странства с мерой доверия. Математическая структура вероятностного про­странства является конкретизацией как математической структуры пространства с мерой доверия, так и математической структуры пространства с мерой правдо­подобия, тем самым реализуется так называемое множественное наследование [2].

Указанные взаимосвязи имеют существенное значение при рассмотрении мате­матических структур пространств с нечеткой мерой.

Литература:

1.      Буч Г., Рамбо Д., Якобсон И. Язык UML. Руководство пользователя.- ДМК-Пресс, 2007.- 496 с.

2.      Леоненков А. В. Нечеткое моделирование в среде MATLAB и fuzzyTECH.-СПб.: БХВ-Петербурr, 2005.- 736 с.

3.      Яхъяева Г.Э.Нечеткие множества и нейронные сети. – М.: Бином. Лаборатория знаний, 2008.- 320 с.