Решение задач о деформировании материала, в которых существенными являются градиенты напряжений, приводит к значительным расхождениям между данными экспериментов и расчетными результатами классической теории упругости. Отчасти поэтому модели сред, которые описывается не только вектором перемещения, но также вектором поворота, получили свое распространение. Такие среды часто называют средами Коссера, а соответствующая теория получила названия моментной или несимметричной теории упругости.
Первые труды, которые можно отнести к микроструктурной теории, принадлежат Фойгту. Он впервые рассмотрел модель среды с вращательным взаимодействием ее частиц при изучении упругих свойств кристаллов. Первая попытка построения теории упругости с несимметричным тензором напряжений принадлежит братьям Коссера. Согласно концепции братьев Коссера, учитывающей вращательное взаимодействие частиц материала, при изучении напряженного состояния твердого деформируемого континуума необходимо наряду с обычными напряжениями (сила на единицу площади) вводить в рассмотрение моментные напряжения (момент силы на единицу площади). В теории среды Коссера для описания перемещения частиц рассматриваемой среды наряду с обычным полем перемещений вводится кинематически независимое поле векторов, характеризующих малые повороты частиц. Таким образом, в этой теории присутствуют две независимых кинематических неизвестных, а тензоры напряжений и моментных напряжений являются несимметричными.
Известны обобщения несимметричной теории на случай термоупругости и больших деформаций. Также известны решения ряда динамических задач распространения и взаимодействия упругих волн в твердых телах с микроструктурой. Очень часто учет вектора внутреннего вращения используется также и в работах по моделированию пластического деформирования материала.
Одним из основных факторов, сдерживающих изучение моделей несимметричных сред, является недостаток информации о материальных константах сред с микроструктурой. Как правило, новые физические константы, определяющие вклад моментных составляющих, задают из области их энергетически допустимых значений.
Систематизированное изложение несимметричной теории упругости приведено в монографии [1]. В статье [2] дается «новая» постановка статической задачи несимметричной теории упругости для изотропной среды. «Новая» постановка заключается в решении двенадцати уравнений второго порядка относительно шести неизвестных компонент тензора напряжений и шести неизвестных компонент тензора моментных напряжений при удовлетворении двенадцати граничным условиям.
Целью данной статьи является нахождение условий эллиптичности «новой» постановки задачи несимметричной теории упругости. Исследование условий эллиптичности «новой» постановки задачи несимметричной теории упругости важно, так как для эллиптических краевых задач характерны регулярность решений соответствующих уравнений и точные априорные оценки, что позволяет говорить о корректности постановки задачи.
1. Новая постановка задачи несимметричной теории упругости.
Уравнения движения. Гладкая поверхность 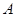 ограничивает произвольную область тела, внутрь которого через бесконечно малый элемент поверхности
ограничивает произвольную область тела, внутрь которого через бесконечно малый элемент поверхности 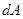 действует вектор сил
действует вектор сил 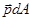 и вектор моментов
и вектор моментов 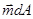 . С учетом вектора массовых сил
. С учетом вектора массовых сил 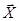 и вектора массовых моментов
и вектора массовых моментов 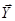 уравнения равновесия для произвольного объема
уравнения равновесия для произвольного объема 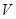 имеют вид [3]
имеют вид [3]
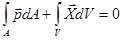 , (1.1)
, (1.1)
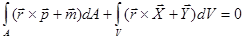 , (1.2)
, (1.2)
где 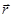 - радиус-вектор, отсчитываемый от некоторой точки тела.
- радиус-вектор, отсчитываемый от некоторой точки тела.
В прямоугольной декартовой системе координат эти уравнения (1.1) и (1.2) перепишутся следующим образом:
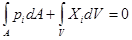 , (1.3)
, (1.3)
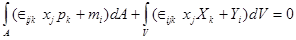 , (1.4)
, (1.4)
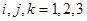 .
.
В качестве объема 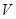 можно выбрать бесконечно малый тетраэдр
можно выбрать бесконечно малый тетраэдр 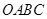 с тремя гранями, ортогональными координатным осям. Тогда
с тремя гранями, ортогональными координатным осям. Тогда 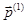 - вектор силовых напряжений, а
- вектор силовых напряжений, а 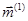 - вектор моментных напряжений, действующие на элемент поверхности
- вектор моментных напряжений, действующие на элемент поверхности 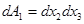 . Соответственно, векторы
. Соответственно, векторы 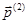 ,
, 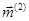 и
и 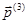 ,
, 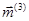 действуют на элементы
действуют на элементы 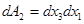 и
и 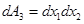 . Составляющие силовых и моментных напряжений обозначаются через
. Составляющие силовых и моментных напряжений обозначаются через 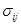 и
и 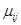 , т.е.
, т.е.
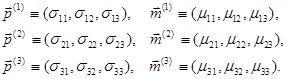 (1.5)
(1.5)
Пусть 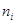 означают компоненты единичного вектора нормали
означают компоненты единичного вектора нормали 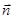 к четвертой грани
к четвертой грани 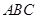 тетраэдра, а
тетраэдра, а 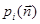 и
и 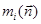 - составляющие сил и моментов, действующих на этой грани. Тогда
- составляющие сил и моментов, действующих на этой грани. Тогда
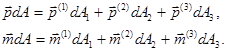 (1.6)
(1.6)
Поскольку
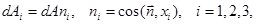 (1.7)
(1.7)
уравнения (1.6) принимают вид
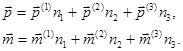 (1.8)
(1.8)
Учитывая (1.5), из соотношений (1.8) получается, что
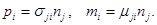 (1.9)
(1.9)
Теперь значения 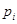 и
и 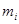 можно подставить в уравнения (1.3) и (1.4), которые примут вид
можно подставить в уравнения (1.3) и (1.4), которые примут вид
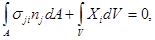 (1.10)
(1.10)
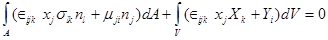 (1.11)
(1.11)
Применение к этим уравнениям теоремы Гаусса-Остроградского о дивергенции приведет к следующим уравнениям:
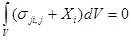 (1.12)
(1.12)
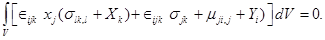 (1.13)
(1.13)
Из (1.12) в силу произвольности объема 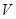 следует, что
следует, что
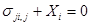 (1.14)
(1.14)
справедливо в каждой точке тела. В силу этого уравнения первый член в подынтегральном выражении (1.13) равен нулю. Так как объем 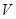 выбран произвольно, справедливо соотношение
выбран произвольно, справедливо соотношение
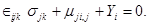 (1.15)
(1.15)
Тензор напряжений 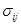 несимметричен. Этот тензор будет симметричен только при отсутствии массовых моментов
несимметричен. Этот тензор будет симметричен только при отсутствии массовых моментов 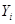 и моментных напряжений
и моментных напряжений 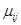 . В этом случае уравнение (1.15) сводится к виду
. В этом случае уравнение (1.15) сводится к виду 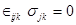 , что обеспечивает в теории симметричной упругости симметрию тензора
, что обеспечивает в теории симметричной упругости симметрию тензора 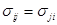 .
.
Уравнения (1.14) и (1.15) являются уравнениями равновесия внутри тела, уравнения (1.9) – на поверхности тела. Соотношения (1.9) можно трактовать и как граничные условия в напряжениях.
«Классическая» постановка задачи несимметричной теории упругости. В дальнейшем вектор массовых сил 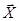 и вектор массовых моментов
и вектор массовых моментов 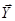 считаются равными нулю. Таким образом, уравнения (1.14) и (1.15) принимают вид
считаются равными нулю. Таким образом, уравнения (1.14) и (1.15) принимают вид
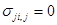 , (1.16)
, (1.16)
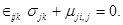 (1.17)
(1.17)
Малые деформации связаны с перемещениями соотношениями Коши
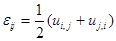 . (1.18)
. (1.18)
Чтобы найти перемещения, необходимо решить систему шести дифференциальных уравнений (1.18) относительно трех неизвестных 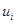 . Необходимым и достаточным условием разрешимости этих уравнений для односвязной области является обращение в нуль симметричного тензора несовместности
. Необходимым и достаточным условием разрешимости этих уравнений для односвязной области является обращение в нуль симметричного тензора несовместности 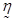 :
:
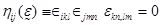 . (1.19)
. (1.19)
Как было сказано во введении, дополнительной кинематической характеристикой для среды Коссера является вектор независимого вращения с компонентами 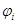 и тензор его градиента
и тензор его градиента 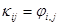 , который называется тензором искривлений. Несимметричные тензоры можно разложить на симметричные и антисимметричные части:
, который называется тензором искривлений. Несимметричные тензоры можно разложить на симметричные и антисимметричные части:
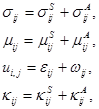 (1.20)
(1.20)
где
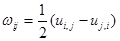 , (1.21)
, (1.21)
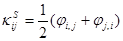 , (1.22)
, (1.22)
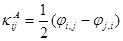 . (1.23)
. (1.23)
Чтобы найти компоненты вектора вращения по известным функциям 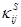 , необходимо решить систему шести дифференциальных уравнений (1.22) относительно трех неизвестных
, необходимо решить систему шести дифференциальных уравнений (1.22) относительно трех неизвестных 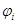 . Необходимым и достаточным условием разрешимости этих уравнений для односвязной области является обращение в нуль симметричного тензора несовместности
. Необходимым и достаточным условием разрешимости этих уравнений для односвязной области является обращение в нуль симметричного тензора несовместности 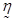 :
:
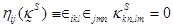 . (1.24)
. (1.24)
Для наглядности результатов определяющие соотношения будут рассматриваться в частном неперекрещивающемся виде:
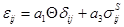 , (1.25)
, (1.25)
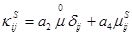 , (1.26)
, (1.26)
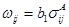 , (1.27)
, (1.27)
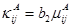 , (1.28)
, (1.28)
где 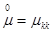 , а
, а 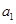 ,
, 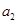 ,
, 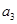 ,
, 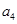 ,
, 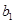 и
и 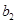 - независимые упругие константы, которые должны находиться экспериментально.
- независимые упругие константы, которые должны находиться экспериментально.
Граничные условия задаются на поверхности 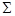 , ограничивающей объем тела:
, ограничивающей объем тела:
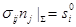 , (1.29)
, (1.29)
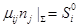 , (1.30)
, (1.30)
где 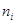 - компоненты единичного вектора нормали к поверхности
- компоненты единичного вектора нормали к поверхности 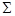 ,
, 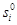 - компоненты заданных на этой поверхности усилий, а
- компоненты заданных на этой поверхности усилий, а 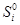 - компоненты заданных на границе моментов.
- компоненты заданных на границе моментов.
«Классическая» постановка задачи несимметричной теории упругости в напряжениях заключается в отыскании 18 компонент тензоров 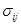 и
и 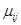 в односвязной области
в односвязной области 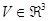 из решения уравнений совместности (1.19), (1.24) с использованием определяющих соотношений (1.25)-(1.28) и уравнений равновесия (1.16), (1.17) при удовлетворении граничным условиям (1.29), (1.30).
из решения уравнений совместности (1.19), (1.24) с использованием определяющих соотношений (1.25)-(1.28) и уравнений равновесия (1.16), (1.17) при удовлетворении граничным условиям (1.29), (1.30).
«Новая» постановка задачи несимметричной теории упругости. Из уравнений совместности (1.19), (1.24) можно получить обобщенные уравнения совместности для несимметричной теории упругости
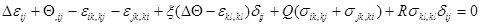 , (1.31)
, (1.31)
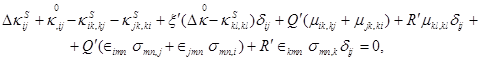 (1.32)
(1.32)
где 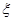 ,
, 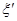 ,
, 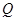 ,
, 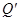 ,
, 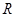 ,
, 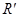 - пока произвольные константы.
- пока произвольные константы.
Теорема. Если уравнения равновесия (1.16), (1.17) удовлетворяются только на границе:
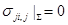 , (1.33)
, (1.33)
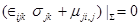 , (1.34)
, (1.34)
то при выполнении условий 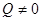 ,
, 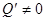 ,
, 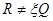 ,
, 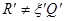 из уравнений (1.31), (1.32) следует, что во всей области
из уравнений (1.31), (1.32) следует, что во всей области 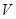 удовлетворяются уравнения равновесия (1.16), (1.17) и уравнения совместности (1.19), (1.24).
удовлетворяются уравнения равновесия (1.16), (1.17) и уравнения совместности (1.19), (1.24).
Обратные определяющие соотношения имеют вид
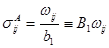 , (1.35)
, (1.35)
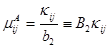 , (1.36)
, (1.36)
где 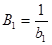 и
и 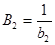 .
.
Градиенты тензоров 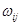 и
и 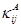 связаны с градиентами тензоров
связаны с градиентами тензоров 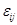 и
и 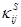 тождествами
тождествами
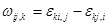 , (1.37)
, (1.37)
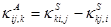 . (1.38)
. (1.38)
После дифференцирования уравнений (1.35) и (1.36) по 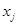 и подстановки соотношений (1.37), (1.38) получается
и подстановки соотношений (1.37), (1.38) получается
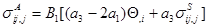 , (1.39)
, (1.39)
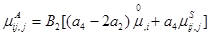 . (1.40)
. (1.40)
Аналогично, после дифференцирования уравнений (1.35) и (1.36) по 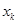 и подстановки соотношений (1.37), (1.38) получается
и подстановки соотношений (1.37), (1.38) получается
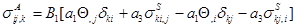 (1.41)
(1.41)
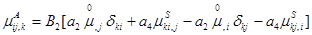 (1.42)
(1.42)
Обобщенные уравнения совместности (1.31), (1.32) с помощью определяющих соотношений (1.25)-(1.28) и тождеств (1.39), (1.40) и (1.41), (1.42) записываются в виде
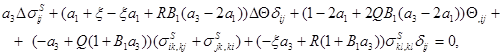 (1.43)
(1.43)
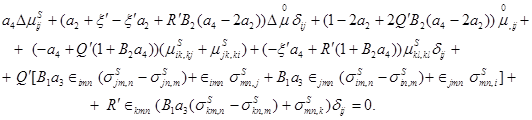 (1.44)
(1.44)
«Новая» постановка задачи заключается в отыскании 12 независимых компонент симметричных тензоров 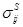 ,
, 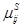 из решения 12 обобщенных уравнений совместности (1.43), (1.44) при удовлетворении шести граничных условий (1.33), (1.34) и шести уравнений равновесия на границе тела (1.29), (1.30).
из решения 12 обобщенных уравнений совместности (1.43), (1.44) при удовлетворении шести граничных условий (1.33), (1.34) и шести уравнений равновесия на границе тела (1.29), (1.30).
2. Условия эллиптичности системы обобщенных уравнений совместности.
Эллиптичность системы дифференциальных уравнений. Пусть задана система уравнений [4] с 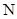 неизвестными функциями
неизвестными функциями 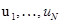 с
с 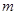 независимыми переменными
независимыми переменными 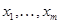 . Эту систему можно записать так:
. Эту систему можно записать так:
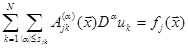 , (2.1)
, (2.1)
Здесь 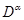 - некоторые линейные дифференциальные выражения
- некоторые линейные дифференциальные выражения 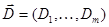 ,
, 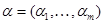 - мультииндекс,
- мультииндекс, 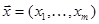 .
.
Если порядок дифференциального выражения равен 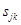 , то можно записать
, то можно записать
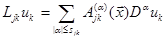 , (2.2)
, (2.2)
где
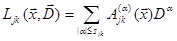 . (2.3)
. (2.3)
Поэтому систему можно представить в виде
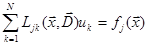 ,
, 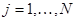 . (2.4)
. (2.4)
Если ввести матрицу 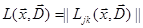 порядка
порядка 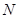 и N-компонентные векторы
и N-компонентные векторы 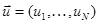 и
и 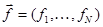 , то система примет матричный вид
, то система примет матричный вид
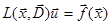 . (2.5)
. (2.5)
Через 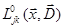 обозначена главная часть полиномиальной матрицы
обозначена главная часть полиномиальной матрицы 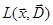 . Она получается, если в формуле (5.3) удержать только члены, у которых
. Она получается, если в формуле (5.3) удержать только члены, у которых 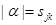 :
:
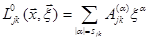 . (2.6)
. (2.6)
Пусть 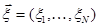 - произвольная точка пространства
- произвольная точка пространства 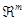 . Можно положить
. Можно положить
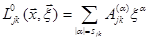 . (2.7)
. (2.7)
При этом
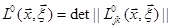 . (2.8)
. (2.8)
Система называется правильно эллиптической, если порядок системы 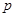 - четное число (
- четное число (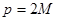 ), и для каждой пары линейно независимых действительных векторов
), и для каждой пары линейно независимых действительных векторов 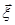 и
и 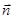 полином
полином 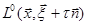 комплексной переменной
комплексной переменной 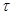 имеет ровно
имеет ровно 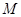 корней с положительной мнимой частью.
корней с положительной мнимой частью.
Эллиптичность системы обобщенных уравнений совместности. Поскольку системы уравнений (4.13), (4.14) не связанные, и главные части соответствующих им полиномиальных матриц имеют одинаковую структуру, достаточно исследовать эллиптичность только первой системы, а для второй условие будет аналогичным.
Главная часть полиномиальной матрицы для системы уравнений (4.13) следующая:
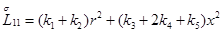 ,
,
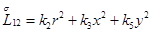 ,
,
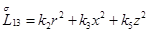 ,
,
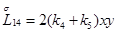 ,
,
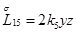 ,
,
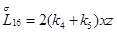 ,
,
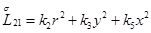 ,
,
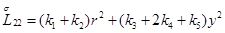 ,
,
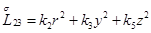 ,
,
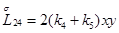 ,
,
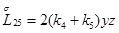 ,
,
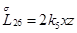 ,
,
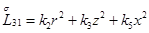 ,
,
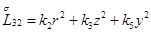 ,
,
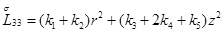 ,
,
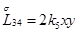 ,
,
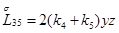 ,
,
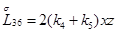 ,
,
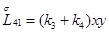 ,
,
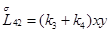 ,
,
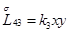 ,
,
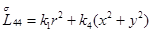 ,
,
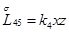 ,
,
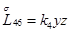 ,
,
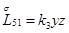 ,
,
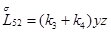 ,
,
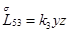 ,
,
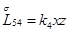 ,
,
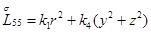 ,
,
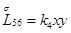 ,
,
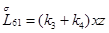 ,
,
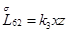 ,
,
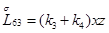 ,
,
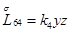 ,
,
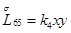 ,
,
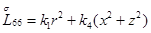 ,
,
где
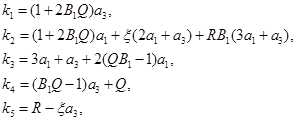
Матрица 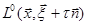 для
для 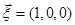 и
и 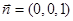 запишется в виде
запишется в виде
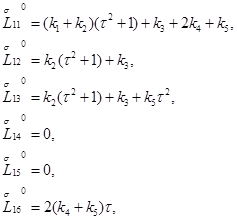
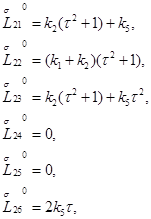
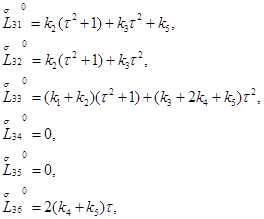
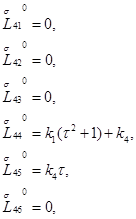
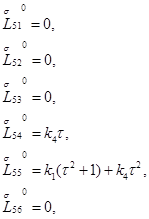
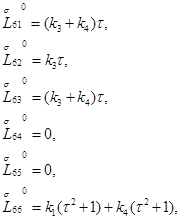
Значение определителя этой матрицы
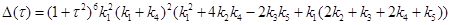
Таким образом, правильная эллиптичность достигается при следующем выборе параметров:
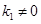 , (2.9)
, (2.9)
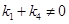 , (2.10)
, (2.10)
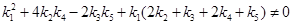 . (2.11)
. (2.11)
Заключение
В работе получены условия эллиптичности «новой» постановки статической задачи несимметричной теории упругости для изотропной среды (3.8)-(3.11) в случае неперекрещивающихся определяющих соотношений. Эти условия указаны в формулах (2.9)-(2.11) и (3.17). Таким образом, проведенное исследование подтверждает корректность «новой» постановки статической задачи несимметричной теории упругости для изотропной среды в случае неперекрещивающихся определяющих соотношений.
Список литературы
1. Nowacki, W. Teoria niesymetrycznej sprężystości / W. Nowacki. – Warsawa: PWN, 1971. – 246 с.
2. Победря, Б.Е. Статическая задача несимметричной теории упругости для изотропной среды / Б.Е. Победря // Вестн. Моск. ун-та. Сер. 1, математика. Механика. – 2005. – № 1. – С. 54–59.
3. Новацкий, В.К. Теория упругости / В.К. Новацкий. – М.: Мир, 1975. – 872 с.
4. Хермандер, Л. Линейные дифференциальные операторы с частными производными / Л. Хермандер. – М.: Мир, 1965. – 379 с.

