Великий среднеазиатский учёный Абу Али ибн Сина, в Европе известен как Авиценна, родился в селении Афшана, недалеко от города Бухары в 980 году (умер в 1037 году). Ибн Сина уже в молодости стал видным учёным и овладел многими профессиями. Он был учёным — энциклопедистом и одарённым врачом — исследователем. Ибн Сина обобщил достижения своих современников и предшественников, а также поставил и разрешил новые научные проблемы. Его научные рукописи и трактаты хранятся в библиотеках ряда стран Европы и Азии.
Ибн Сина, основными научными специальностями которого были философия и медицина, творчески работал и в области математических наук.
Большой интерес представляет его трактат «Книга знания» [1].
«Книга знания» (Донишома) великого среднеазиатского учёного эпохи Средневековья Абу Али ибн Сины (Авиценны) представляет собой краткую энциклопедию философских, логических, физических и математических знаний, написанную на его родном языке — языке фарси–дари. Эта книга аналогична его книге на арабском языке, озаглавленной «Книга спасения» (Китаб ан-наджат), математические главы которой весьма близки к соответственным «Книги знаний». Математические главы «Книги звания», дошедшие до нас, представляют собой краткое изложение геометрии, астрономии, арифметики и музыки. Эти главы очень интересны для истории науки как выбором материала, так и освещением его, а в геометрической части, где все предложения приводятся с доказательствами, сравнивая их с методами доказательств Евклида. Геометрическая глава «Книги знания» состоит из 12 разделов. Приведём некоторые разделы: первый раздел о началах геометрии, относящихся к пересекающимся линиям. Учёный приводитописание взаимного положения прямых между собой и плоскостью в пространстве с их изображением на чертеже: — Если одна линия пересекает другую, то она может не наклоняться ни в одну из сторон. Пусть, например, (рис. 1) линия СD пересекает линию АВ в точке С. Образуемые с двух сторон этой линией углы — угол DСА и угол DСВ равны; линия СD называется перпендикуляром, а оба угла — прямыми углами.
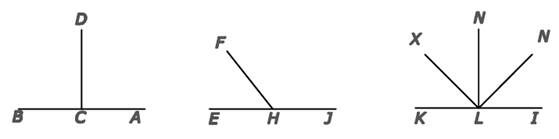
Рис. 1. Рис. 2. Рис. 3.
Она может также наклоняться в одну из сторон. Так, (рис. 2) линия FН, пересекая линию GЕ, наклоняется к Е. Поэтому угол FНЕ меньше прямого угла и называется острым углом, а угол GНЕ больше прямого угла и называется тупым углом. Насколько один угол меньше прямого угла, — настолько другой — больше его, вместе эти два угла равны двум прямым углам; их можно делить как угодно — полученные таким образом два угла вместе всегда будут равны двум прямым углам.
Если линия МL (рис. 3) пересекает линию КI то образуются два угла; два угла образуются также линией LN и линией LХ; между каждой парой соседних линий находится целый угол, а между каждой парой линий, не являющихся соседними, находится угол, разделенный линией, проходящей между этими двумя линиями. Таким образом, здесь имеется четыре угла, составляющих вместе два прямых угла; к этим четырем углам можно прибавить еще несколько — утверждение останется тем же.
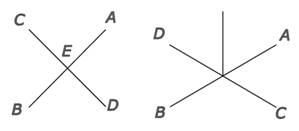
Рис. 4. Рис. 5.
Если одна линия падает на другую, (рис. 4) пересекая ее и проходя далее, например, если прямые АВ и СD пересекаются в точке Е, то их пересечение образует четыре угла: по два смежных и два вертикальных. Вертикальные углы, получающиеся при пересечении равны, и очевидно, что по мере увеличения одного утла вертикальный по отношению к нему угол увеличивается на столько же, а по мере уменьшения одного угла вертикальный по отношению к нему угол на столько же уменьшается.
Если две линии пересекаются на плоскости, а третья линия падает перпендикулярно в точку пересечения этих линий, то эта третья линия перпендикулярна ко всякой линии, проведённой через точку пересечения на данной плоскости (рис. 5.); такова, например, линия GЕ падающая в точку пересечения АВ и СD из взятой в пространстве точки G, так как если бы эта линия не была перпендикулярной к третьей линии, находящейся на данной плоскости, то она наклонялась бы в одну из сторон к этой плоскости, а следовательно, наклонялась бы в одну из сторон к четырем линиям, составляющим линии АВ и СD и, значит, не была бы перпендикулярна к ним, что нелепо.
Обратно, всякая линия в пространстве, перпендикулярная к линии, находящейся на плоскости, и перпендикулярная ко всякой линии, проведенной из точки пересечения этих двух линий [на плоскости], называется перпендикуляром к этой плоскости.
Две линии, перпендикулярные к плоскости, параллельны между собой, потому что если бы одна из этих двух линий отклонилась к другой, то она отклонилась бы в одну из сторон дайной плоскости и, значит, не была бы перпендикулярной к этой плоскости. Сравнивая положения, приведённые Ибн Синой, приходим к выводу, что можно применить этот раздел при преподавании современной элементарной геометрии, а также по предмету «Начертательная геометрия» [2] по соответствующей теме «Позиционные свойства геометрических образов».
Рассмотрим четвертый раздел о построениях при помощи циркуля и линейки. В этом разделе Ибн Сина приводит построение перпендикуляра из точки на прямую, и деление отрезка на две равные части, причём чертёжными инструментами (учёный называет циркуль — паркар, а линейку — мастара): — Если мы хотим восстановить перпендикуляр в точке С, находящейся на линии АВ, то отметим циркулем по обе стороны от точки С два равных отрезка, например СD и СЕ (рис. 6). Из центра D опишем часть окружности на
расстоянии DЕ, например ЕG. Таким же образом из центра Е опишем часть окружности на расстоянии ЕD, например, DG. Эти окружности пересекутся в точке G. Из точки G проведем линей кой линии GD, GЕ и GС. Мы утверждаем, что линия GС является перпендикуляром, восстановленным в точке С, находящейся на линии АВ,
так как стороны треугольника GDЕ равны, поскольку обе они отложены циркулем на одном и том же расстоянии. Таким образом построен равносторонний треугольник. Кроме того, стороны треугольника GDС равны сторонам треугольника GЕС, каждая равна своей соответственной. Поэтому угол GСD равен углу GСЕ, следовательно, линия GС перпендикулярна линии АВ.
Если же точка С находится не на линии АВ (рис. 7), а вне ее, и мы хотим из этой точки С опустить перпендикуляр на линию АВ, то по другую сторону линии АВ отметим произвольную точку D; из центра С опишем часть окружности на расстоянии СD; эта окружность пересечёт линию АВ в двух точках Е и G; линию ЕG разделим пополам в Н и проведем линию СН; мы утверждаем, что она является перпендикуляром. В самом деле, если мы проведем линии СЕ и СG, то будет как в предыдущем предложении.
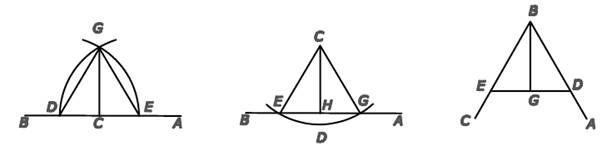
Рис. 6 Рис. 7 Рис. 8
Если мы хотим разделить угол АВС пополам (рис. 8), то отложим циркулем линию ВD, равную линии ВЕ, точку Е соединим с точкой D, а затем разделим линию ЕD в точке D пополам. Эти способы построений соответствуют теме «Геометрическое черчение» при преподавании предмета «Инженерная графика».
Ибн Сина, несмотря на трудности того времени, был новатором и передовым учёным своего времени, верил в непобедимую силу разума– создал огромное количество научных рукописей и трактатов в виде учебных пособий, которые служили источниками знаний, применялись для практического применения его учениками и людьми, стремившимися к грамоте, знаниям и профессиям. Ибн Сина был уважаемым педагогом — у него было множество учеников, которым он передавал свои знания и умения. Он был великим целителем, которому были равны и бедные и богатые. Вполне возможно, что по его научным трактатам обучались землемеры, ремесленники и зодчие, создавшие в эпоху Средневековья неповторимые шедевры архитектурного зодчества Востока и Средней Азии. Как видим из выше изложенного, работая в области различных наук, Ибн Сина внёс огромный вклад в развитие мировой науки. Его научные труды можно использовать при преподавании современных научных дисциплин, не только как исторический, но и тематический материал.
Литература:
1. Абу Али ибн — Сина. Математические главы «Книги знания (Донишнома)». — Душанбе: Ирфон, 1967.
2. Чекмарёв А. А. Начертательная геометрия и черчение. — Москва. 2002 г.

