Полное имя ал-Хорезми — Абу Абдаллах Мухаммад ибн Мусса ал-Хорезми. Принято считать годом его рождения 783 г, а годом его смерти 850 год. Родиной учёного является Хорезм, которому соответствует территория современной Хорезмской области Республики Узбекистан. В Хорезме к началу IX века сложились традиции древней и самобытной культуры. Свидетельство этому мы находим в трудах средневековых историков, а также благодаря археологическим раскопкам. Ал-Хорезми принадлежал к тем среднеазиатским учёным, которые были привлечены в Багдад для работы в «Доме мудрости» — учреждение, выполнявшее функции Академии наук, основанным правителем ал-Мамуном. При изучении данных о жизни и творчестве ал-Хорезми историки науки основывались главным образом на исследовании его трудов. Многообразные научные интересы ал-Хорезми касались математики, астрономии, географии и истории. Алгебраический трактат ал-Хорезми известен под заглавием: «Краткая книга восполнения и противопоставления» (по-арабски: «Китаб мухтасар ал-джабр ва-л-мукабала»). Трактат состоит из двух частей — теоретической и практической. В первой из них излагается теория линейных и квадратных уравнений, а также затрагиваются некоторые вопросы геометрии. Учёные в средние века уделяли большое внимание геометрии. Особый интерес вызывали «Начала» Евклида. Это классическое произведение было переведено на арабский язык уже в конце VIII — начале IX в. По нему изучали геометрию, его обсуждали и комментировали. Наряду с вопросами теории их занимали и проблемы практической геометрии. Такие проблемы постоянно приходилось решать землемерам, ремесленникам, строителям. Поэтому математики писали специальные сочинения, которые служили руководствами для практиков. В них обычно не было доказательств, а приводились только определения основных геометрических понятий и правила измерения фигур и тел. Правила обычно разъяснялись на многочисленных конкретных примерах.
Впервые в литературе на арабском языке такое собрание сведений, необходимых в практической, хозяйственной деятельности человека, дал ал-Хорезми. Этим вопросам посвящен геометрический раздел его «Алгебры». Он носит название «Глава об измерении». Основное внимание в ней уделено вопросам измерения фигур.
Вначале ал-Хорезми вводит понятие единичной площади и дает правила вычисления площади квадрата, треугольника и ромба. Он рассматривает равносторонний треугольник, но формулирует правило, справедливое для треугольника любого вида: «Если перемножить высоту и половину основания, на которое падает высота, получится площадь этого треугольника». Относительно ромба ал-Хорезми говорит: «Если ты умножишь одну из диагоналей на половину другой, получиться его площадь».
Ал-Хорезми вычисляет площадь сегмента круга, которую он называет площадью, соответствующей дуги. Для этого вводится длина s дуги AB, хорда а и высота сегментаDC=h, носившая название «стрела дуги» (рис. 1).
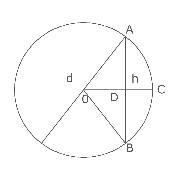
Рис. 1
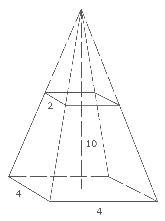
Рис. 2
Следующий вопрос, который рассматривает ал-Хорезми, касается объемов тел — параллелепипеда, кругового цилиндра, призмы, конуса, пирамиды.
Относительно параллелепипеда (который называется «четырехугольным телом») он говорит: «Если умножишь длину на ширину, а затем на высоту, получится объем».
Объем цилиндра, треугольной, четырехугольной и т. д. призмы определяется умножением площади основания на высоту. «Если же тело не четырехугольное, — пишет ал-Хорезми, — а круглое, треугольное или иное, но его грани параллельны высоте, его мера такова: измерь его плоскую фигуру, т. е. узнай ее площадь, умножь это на глубину, получится объем».
Конусы и пирамиды измеряются по следующему правилу: «Что касается конусов треугольного, квадратного и круглого, то они таковы, что произведение трети площади их основания на высоту есть их объём».
В геометрическом разделе книги ал-Хорезми рассматривает правило вычисления объёма усечённой квадратной пирамиды с данными основаниями и высотой. Пусть высота усеченной пирамиды h=10, сторона нижнего основания a1=4, а верхнего a2=2 (рис.2).
Высота неусеченной пирамиды H определяется следующим образом:
![]() ,
, ![]() ,
, ![]() .
.
Тогда объем неусеченной пирамиды ![]() , а объем верхней пирамиды
, а объем верхней пирамиды ![]() .
.
Искомый объем усеченной пирамиды υ определяется как разность этих двух объемов:
![]() .
.
Наиболее подробно ал-Хорезми останавливается на вопросах, связанных с измерением треугольников и четырехугольников. Он начинает с формулировки и доказательства теоремы Пифагора. Это единственный в сочинении случай, когда геометрическое предложение доказано строго в духе «Начал» Евклида. Однако доказательство проводится только для равнобедренного прямоугольного треугольника.
Ал-Хорезми пишет: «Знай, что каждый прямоугольный треугольник таков, что если умножить каждую из его коротких сторон на себя, то сумма произведений равна произведению длинной стороны на себя».
Воспроизводим ход его рассуждения. Построим квадрат ACDB (рис.3).
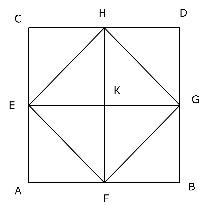
Рис. 3
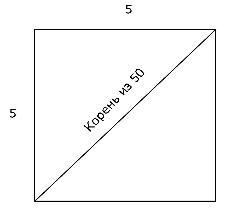
Рис. 4
Разделим сторону ACпополам в точке E и проведем EG┴AC. Затем разделим пополам сторону AB в точке F и проведем из нее FH┴AB. Тогда данный квадрат будет разбит на четыре меньших квадрата, равных между собой. Проводим диагонали FE, EH, HG, GF, рассекающие каждый из этих квадратов на два равных прямоугольных равносторонних треугольника. В результате данный большой квадрат оказывается разбитым на восемь таких треугольников, равных между собой. Следовательно, четыре из них составляют квадрат EHGF, равный половине большого квадрата.
Один из разделов геометрической главы сочинения ал- Хорезми посвящён классификации четырёхугольников и вычислению их площадей. Выделено пять видов четырёхугольников: 1) квадрат, 2) прямоугольник, 3) ромб, 4) параллелограмм, не являющийся прямоугольником, 5) четырёхугольник с разными сторонами и углами.
Правила вычисления площадей и примеры к ним сформулированы так, что они могут служить руководством для практиков-землемеров.
Например, относительно измерения квадрата и прямоугольника ал- Хорезми пишет: «Что касается четырёхугольников с равными сторонами и прямыми углами или с разными сторонами и прямыми углами, то, чтобы получить их площадь, умножь длину и ширину, то, что, получится, и есть площадь. Например, каждая сторона четырёхугольного участка земли есть пять локтей, тогда его площадь — двадцать пять локтей. Вот чертеж этого» (рис.4).
В целях исследования истории науки геометрии, мы рассмотрели некоторые геометрические задачи ал- Хорезми. Как видно из вышеизложенного, мы видим, что эти задачи обоснованы и имеют практический характер. Творчество Мухаммада ибн Муса ал- Хорезми занимает важное место среди учёных Средней Азии, имена которых вошли в историю точного естествознания. В IX веке — на заре расцвета средневековой восточной науки — учёный внёс большой вклад в развитие арифметики, алгебры, геометрии, астрономии, географии. Труды ал-Хорезми оказывали влияние на учёных Востока и Запада. Исследованием творчества ал-Хорезми занимались многие историки науки. В процессе обучения и воспитания подрастающего поколения, при изучении истории естественных наук, наряду с другими великими учёными, необходимо ознакомить их с творчеством ал- Хорезми.
Литература:
- Мухаммад ибн Мусо ал-Хоразмий. Танланган асарлар (Избранные произведения). Изд-во «Фан», Тащкент-1983.

