Рассматриваемая нами строфоида представляет собой частный, так называемый косой строфоид, на стереометрическом способе образования которой мы и хотим и остановится.
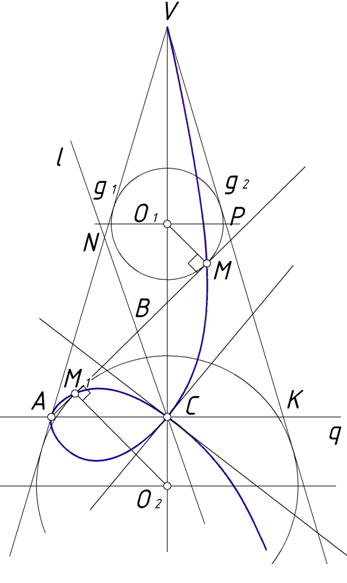
Рис. 1.
Представим себе конус с вершиной в точке V, образующими g1 иg2 икасательной к нему, проходящей через точку А перпендикулярно к g1 (рис. 1). Проведем секущую плоскость через эту касательную, и пусть точки М и М1будут фокусами полученного сечения. Представим теперь, что секущая плоскость поворачивается вокруг касательной, тогда точки М и М1опишут кривую, называемую косой строфоидой, которая будет лежать в плоскости, перпендикулярной к нашей касательной. Для определения положения образующих точек М и М1на прямой АР, являющейся линей пересечения секущей плоскости с плоскостью чертежа, достаточно, как известно, вписать в конус два шара, касающихся секущей плоскости; точки касания и будут фокусами конического сечения, т. е. точками М и М1. Построение кривой может быть однако упрощено и целиком переведено на плоскость чертежа на основании нижеследующих соображений. Обозначив середину отрезка АР через В замечаем, что точки, аналогичные В, будут лежать на прямой l, параллельной образующей g2. Очевидно, эта прямая пройдет также через точки N и С, являющиеся серединами отрезков AV иAK, причем точка К выбрана так, что AV=AK. Если обозначить теперь VA=a, VP=b иAP=c, то будем иметь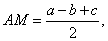
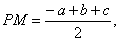 и так как
и так как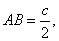 то
то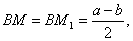 по
по 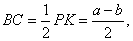 и следовательно,
и следовательно, 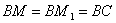 .
.
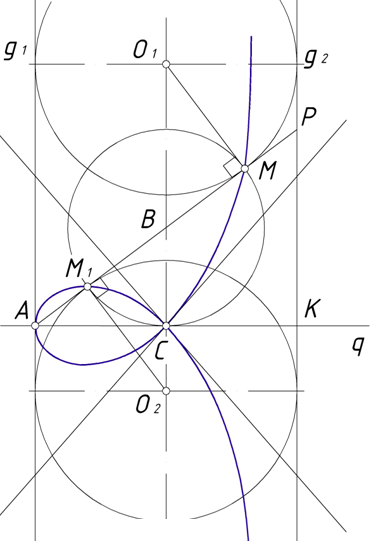
Рис. 2.
Получение соотношение определяет планиметрический способ построения косой строфоиды: пусть дан угол с вершиной в точке С; берем на одной из его сторон точку А и проводим через нее произвольный луч, который пересечет другую сторону в точке В; тогда точки М и М1этого луча, построенные так, что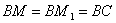 принадлежать строфоиде.
принадлежать строфоиде.
Рассмотренная нами прежде строфоида, в отличие от косой строфоиды, называется прямой. Она может быть получена, если вместо конуса взять цилиндр; именно, надо взять две параллели g1 иg2 на первой из них — точку А; провести затем прямую АР и на ней найти точки касания двух кругов, касающихся параллелей g1 иg2. Найденный точки будут принадлежать строфоиде (рис. 2). Построение можно упросить: пусть В — середина АР, геометрическое место точек В будет, очевидно, осью р цилиндра; если провести теперь через точку А прямую АК, перпендикулярную к g2, то треугольники ВМО1, ВМ1О2 и ВСА окажутся равными между собой следовательно, 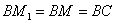 .
.
Способ построения прямой строфоиды на основание полученного равенств очевиден. Справедливость этого равенства убеждает нас также в том, что полученная кривая действительно является строфоидой, так как оно соответствует исходному определению этой кривой.
Убедится в том, что косая строфоида является обобщением прямой, модно также, составив уравнение косой строфоиды. Обозначим с этой целью угол ACN через α, точку A будем считать полюсом, а прямую АК — полярной осью; тогда из треугольники ABC (рис.1) получим;
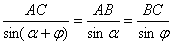 , откуда
, откуда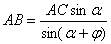 ,
, 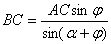 , а так как радиусы-векторы точек М и М1 принадлежащих строфоиде, определяются равенством
, а так как радиусы-векторы точек М и М1 принадлежащих строфоиде, определяются равенством 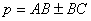 , то полярное уравнение косой строфоиды запишется в виде
, то полярное уравнение косой строфоиды запишется в виде
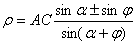 .
.
Полагая здесь 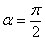 , получим уравнение прямой строфоиды.
, получим уравнение прямой строфоиды.
Литература:
1. А. В. Бубенников. «НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ» Москва «Высшая школа» 1981 г.
2. А. А. Савелов «ПЛОСКИЕ КРИВЫЕ» систематика, свойство, применения. «Москва» 1960 г.

