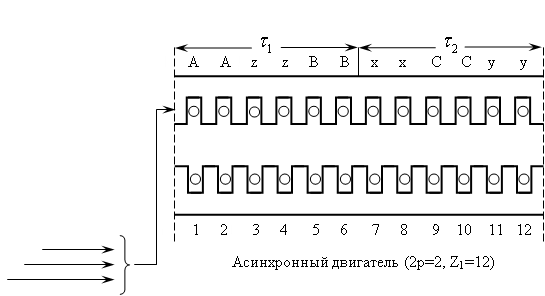
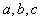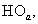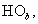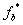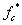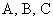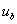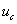В работе [1] рассматривался процесс математического моделирования асинхронного двигателя (2p = 2, Z1 = 12) на основе магнитных схем замещения. Питание обмотки индуктора (соединение «звезда» без нулевого провода, классический тип укладки обмотки) осуществлялось от источника трехфазного синусоидального напряжения.
В данной работе рассматривается процесс математического моделирования асинхронного двигателя (АД) при питании от трехфазного автономного инвертора напряжения с широтно-импульсной модуляцией (АИН ШИМ). Результаты этой работы будут основой для создания учебно-лабораторной установки по исследованию системы АИН ШИМ – АД.
Функциональная схема системы трехфазный автономный инвертор с ШИМ – асинхронный двигатель приведен на рис. 1.
В этой схеме приняты следующие обозначения:
- 
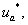и 
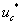- задающие гармонические воздействия:
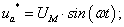
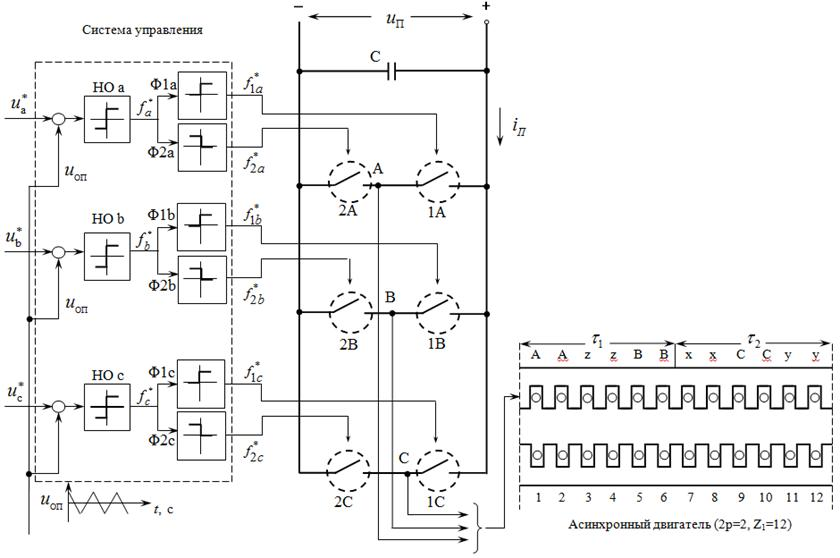
Рис. 1. Функциональная схема системы «АИН ШИМ – АД»
 |
|||||||||
 |
|||||||||
 |
|||||||||
 |
|||||||||
 |
|||||||||
- 
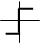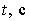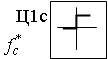
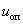– опорное напряжение, представляющее собой пилообразное, двухстороннее, симметричное напряжение с частотой модуляции значительно превышающей частоту напряжения задания;
- 
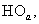и 
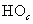– нуль-органы, обеспечивающие сравнение сигналов задания с опорным сигналом. Если 
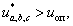то выходные сигналы нуль-органов 
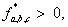иначе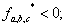 
-
|
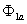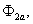
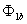и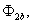 
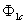и 
и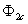 
– формирователи сигналов управления силовыми ключами. Формирователи сигналов управления имеют взаимно инверсные релейные характеристики [2] и сепаратируют сигнал нуль-органа НО по двум каналам управления ключами инвертора. Кроме того предусматривают небольшие временные задержки включения ключей. Это необходимо для предотвращения коротких замыканий источника постоянного напряжения 
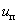через силовые ключи инвертора.- 
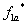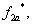
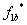и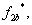 
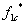и 
и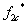 
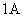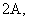
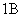- дискретные выходные сигналы с формирователей, управляющих включением силовыми ключами.
- 
и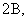 
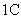и 
и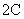 
– силовые ключи попеременно подключающие обмотки фаз двигателя к разноименным полюсам источника постоянного напряжения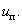 
Цифровой алгоритм расчета опорного сигнала ШИМ приведен в работе [3]. Программирование выходных сигналов нуль-органов произведен в MATLAB и имеет следующий вид:
dt=0.00001;
U0=1;
tau=0;
time=0;
u0p(1)=1;
pwm=-2;
f_sin=50;
f_triangle=1000;
for i=1:8000
tau(i+1)=tau(i)+dt*f_triangle;
time(i+1)=time(i)+dt;
s(i+1)=3*sin(2*pi*f_sin*time(i+1));
s_pi3(i+1)=3*sin(2*pi*f_sin*time(i+1)+pi/3);
if tau(i+1)>=1
tau(i+1)=tau(i+1)-1;
end
if (tau(i+1)>=0) && (tau(i+1)<0.5)
f(i)=1-4*tau(i+1);
else
f(i)=4*tau(i+1)-3;
end
u0p(i+1)=U0*f(i);
if (s(i+1)>=u0p(i+1))
pwm(i+1)=2;
else
pwm(i+1)=-2;
end
if (s_pi3(i+1)>=u0p(i+1))
pwm_pi3(i+1)=2;
else
pwm_pi3(i+1)=-2;
end
end
subplot(2,1,1);
plot(time,s,time,u0p,time,pwm);
hold on;
axis([0 0.04 -4 4]);
subplot(2,1,2);
plot(time,s_pi3,time,u0p,time,pwm_pi3);
hold on;
axis([0 0.04 -4 4]);
Результаты сравнений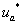 
с 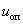для двух значени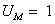й (
и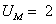 
) приведены на рис. 2 и рис. 3 соответственно (сплошными линиями обозначены выходные сигналы 
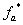с нуль-органа).
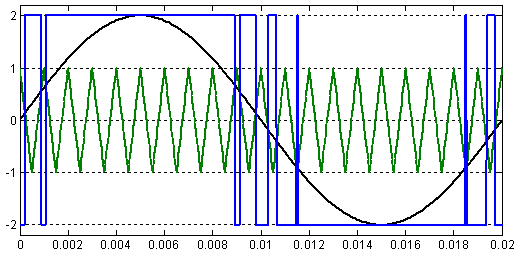
Рис. 2. Сигнал на выходе нуль-органа 
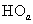при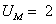
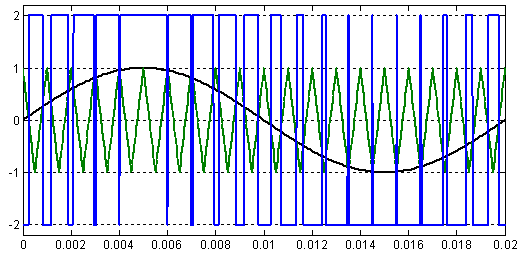
Рис. 3. Сигнал 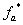на выходе нуль-органа 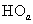при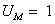
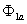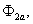
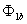Формирователи сигналов управления силовыми ключами ( и 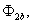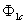и и 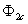) задают программу подключения фаз обмоток двигателя к источнику постоянного напряжения 
.
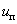Фазное напряжение в обмотке двигателя представляет собой пятиуровневую импульсную функцию [2] со значениями:
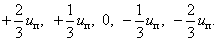
Импульсные напряжения подаваемые на двигатель и 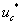связаны с постоянным напряжением 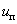и выходными сигналами нуль-органов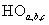 
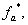и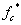 
по следующей зависимости [2]:
Уравнения (*) для решения в программном пакете MATLAB примут следующий вид:
dt=0.00001;
U0=1;
tau=0;
time=0;
u0p(1)=1;
pwm=-1;
um=2;
f_sin=50;
f_triangle=1000;
Um=310/2;
up=Um;
for i=1:8000
tau(i+1)=tau(i)+dt*f_triangle;
time(i+1)=time(i)+dt;
s(i+1)=um*sin(2*pi*f_sin*time(i+1));
s_2pi3(i+1)=um*sin(2*pi*f_sin*time(i+1)+2*pi/3);
s_4pi3(i+1)=um*sin(2*pi*f_sin*time(i+1)+4*pi/3);
if tau(i+1)>=1
tau(i+1)=tau(i+1)-1;
end
if (tau(i+1)>=0) && (tau(i+1)<0.5)
f(i)=1-4*tau(i+1);
else
f(i)=4*tau(i+1)-3;
end
u0p(i+1)=U0*f(i);
if (s(i+1)>=u0p(i+1))
pwm(i+1)=2;
else
pwm(i+1)=-2;
end
if (s_2pi3(i+1)>=u0p(i+1))
pwm_2pi3(i+1)=2;
else
pwm_2pi3(i+1)=-2;
end
if (s_4pi3(i+1)>=u0p(i+1))
pwm_4pi3(i+1)=2;
else
pwm_4pi3(i+1)=-2;
end
PWM(i+1)=up*(1/2)*((2*(pwm(i+1)))/3-(pwm_2pi3(i+1))/3-(pwm_4pi3(i+1))/3);
PWM_2pi3(i+1)=up*(1/2)*(-pwm(i+1)/3+(2*pwm_2pi3(i+1))/3-pwm_4pi3(i+1)/3);
PWM_4pi3(i+1)=up*(1/2)*(-pwm(i+1)/3-pwm_2pi3(i+1)/3+(2*pwm_4pi3(i+1))/3);
end
plot(time,PWM);
axis([0 0.02 -250 250]);
Результаты расчета фазного напряжения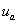 
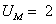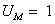для задающих сигналов с и приведены на рис. 4 и рис. 5 соответственно.
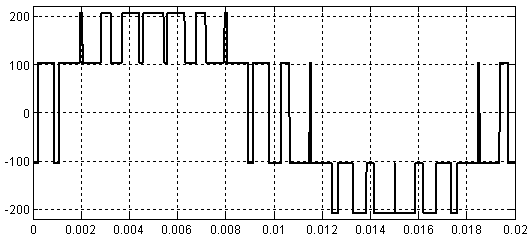
Рис. 4. Импульсное напряжение в фазе обмотки при амплитуде задающего сигнала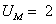
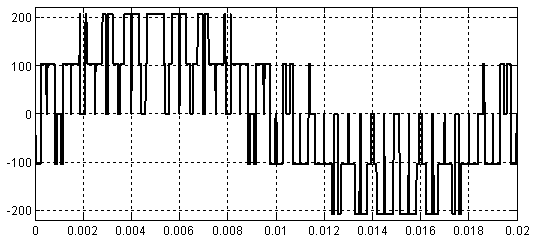
Рис. 5. Импульсное напряжение в фазе обмотки при амплитуде задающего сигнала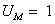
Одна из возможных реализаций математической модели системы «АИН ШИМ - АД» на языке высокого уровня MATLAB примет следующий вид:
% Математическая модель расчета асинхронного двигателя
% методом Гаусса-Жордана
function AD_q_2
% Начальные условия
Rb=0.1003*10^7;
rs=4.75;
Ls=0.074*0.25;
rr=(9.269*10^-5)*0.75;
tau=0;
time=0;
Lr=(0.0372*10^-5)*0.00625;
dt=0.00001;
tz=9.769*10^-3;
m=3.8*0.3;
v0=0;
wn=200;
f=50;
U=wn/dt;
X=zeros(15,1);
F=0;
um=1;
kinv=190*0.5;
% Начальные условия для ШИМ
U0=1;
u0p(1)=1;
pwm=-1;
f_triangle=1000;
f_sin=50;
K=input('длительность цикла k=');
for k=1:(K+1)
% ШИМ
tau(k+1)=tau(k)+dt*f_triangle;
time(k+1)=time(k)+dt;
s(k+1)=um*sin(2*pi*f_sin*time(k+1));
s_2pi3(k+1)=um*sin(2*pi*f_sin*time(k+1)+2*pi/3);
s_4pi3(k+1)=um*sin(2*pi*f_sin*time(k+1)+4*pi/3);
if tau(k+1)>=1
tau(k+1)=tau(k+1)-1;
end
if (tau(k+1)>=0) && (tau(k+1)<0.5)
f(k)=1-4*tau(k+1);
else
f(k)=4*tau(k+1)-3;
end
u0p(k+1)=U0*f(k);
if (s(k+1)>=u0p(k+1))
pwm(k+1)=2;
else
pwm(k+1)=-2;
end
if (s_2pi3(k+1)>=u0p(k+1))
pwm_2pi3(k+1)=2;
else
pwm_2pi3(k+1)=-2;
end
if (s_4pi3(k+1)>=u0p(k+1))
pwm_4pi3(k+1)=2;
else
pwm_4pi3(k+1)=-2;
end
PWM(k+1)=kinv*(1/2)*((2*(pwm(k+1)))/3-(pwm_2pi3(k+1))/3-(pwm_4pi3(k+1))/3);
PWM_2pi3(k+1)=kinv*(1/2)*(-pwm(k+1)/3+(2*pwm_2pi3(k+1))/3-pwm_4pi3(k+1)/3);
PWM_4pi3(k+1)=kinv*(1/2)*(-pwm(k+1)/3-pwm_2pi3(k+1)/3+(2*pwm_4pi3(k+1))/3);
PWM_linear(k+1)=sqrt(3)*PWM(k+1);
PWM_2pi3_linear(k+1)=sqrt(3)*PWM_2pi3(k+1);
v(1,k)=v0; % создание вектор-строки для графика скорости
f(1,k)=sum(F); % Создание вектор-строки для графика усилия
% Создание матрицы А
A=zeros(15);
B=2*Rb*(rr+Lr/dt)+1/dt;
C=-Rb*(rr+Lr/dt)+(2*Rb*Lr+1)*v0/(2*tz);
D=-Rb*Lr*v0/(2*tz);
E=-Rb*(rr+Lr)-(2*Rb*Lr+1)*v0/(2*tz);
T=-wn*Lr*v0/(2*tz);
F1=-wn*(rr+Lr/dt);
M=F1+T;
N=-T+F1;
KS=rs+Ls/dt;
W=-wn*Lr/dt;
P=-Rb*Lr/dt;
Q=(2*Rb*Lr+1)/dt;
% Заполнение матрицы сопротивлений
for n=1:12
A(n,n)=B;
end;
for n=1:11
A(n,n+1)=C;
A(n+1,n)=E;
end;
for n=1:10
A(n,n+2)=D;
A(n+2,n)=-D;
end;
for n=1:2
A(n,n+10)=-D;
A(n+10,n)=D;
end;
A(1,12)=E;
A(12,1)=C;
% Заполнение столбцов 13,14 и 15 матрицы А
for n=1:2
A(4-n,n+12)=-T;
A(6-n,n+13)=T;
A(10-n,n+12)=T;
A(12-n,n+13)=-T;
A(n,13)=(2-n)*M+(n-1)*N;
A(n+2,14)=(n-2)*M+(1-n)*N;
A(n+4,15)=(2-n)*M+(n-1)*N;
A(n+5,13)=(n-2)*T+(1-n)*M;
A(n+8,14)=(2-n)*M+(n-1)*N;
A(n+10,15)=(n-2)*M+(1-n)*N;
end;
A(1,15)=T;
A(7,15)=-T;
A(8,13)=-N;
A(12,13)=T;
for n=1:2
A(12+n,12+n)=((-1)^(n+1))*KS;
A(12+n,15)=((-1)^n)*KS;
end;
for n=1:3
A(15,n+12)=1;
end;
% Заполнение строк 13 и 14 матрицы А
for n=1:4
A(13,n+4)=-U;
A(14,n+2)=U;
A(14,n+8)=-U;
end;
for n=1:2
A(13,n)=U;
A(13,n+10)=U;
end;
% Матрица свободных членов
S=[W*X(13)+P*(X(12)+X(2))+Q*X(1);
W*X(13)+P*(X(1)+X(3))+Q*X(2);
W*(-1)*X(14)+P*(X(2)+X(4))+Q*X(3);
W*(-1)*X(14)+P*(X(3)+X(5))+Q*X(4);
W*X(15)+P*(X(4)+X(6))+Q*X(5);
W*X(15)+P*(X(5)+X(7))+Q*X(6);
W*(-1)*X(13)+P*(X(6)+X(8))+Q*X(7);
W*(-1)*X(13)+P*(X(7)+X(9))+Q*X(8);
W*X(14)+P*(X(8)+X(10))+Q*X(9);
W*X(14)+P*(X(9)+X(11))+Q*X(10);
W*(-1)*X(15)+P*(X(10)+X(12))+Q*X(11);
W*(-1)*X(15)+P*(X(11)+X(1))+Q*X(12);
(X(1)+X(2)-X(5)-X(6)-X(7)-X(8)+X(11)+X(12))*U+(Ls/dt)*(X(13)-X(15))+PWM_2pi3_linear(k+1);
(X(5)+X(6)-X(11)-X(12)-X(9)-X(10)+X(3)+X(4))*U+(Ls/dt)*(X(15)-X(14))+PWM_linear(k+1);
0];
% Решение методом Гаусса-Жордана
Z=rref([A S]);
X=Z(1:15,16:16);
% Матрица токов ротора
Ir=[-wn*X(13)-Rb*X(12)+2*Rb*X(1)-Rb*X(2);
-wn*X(13)-Rb*X(1)+2*Rb*X(2)-Rb*X(3);
-wn*(-1)*X(14)-Rb*X(2)+2*Rb*X(3)-Rb*X(4);
-wn*(-1)*X(14)-Rb*X(3)+2*Rb*X(4)-Rb*X(5);
-wn*X(15)-Rb*X(4)+2*Rb*X(5)-Rb*X(6);
-wn*X(15)-Rb*X(5)+2*Rb*X(6)-Rb*X(7);
-wn*(-1)*X(13)-Rb*X(6)+2*Rb*X(7)-Rb*X(8);
-wn*(-1)*X(13)-Rb*X(7)+2*Rb*X(8)-Rb*X(9);
-wn*X(14)-Rb*X(8)+2*Rb*X(9)-Rb*X(10);
-wn*X(14)-Rb*X(9)+2*Rb*X(10)-Rb*X(11);
-wn*(-1)*X(15)-Rb*X(10)+2*Rb*X(11)-Rb*X(12);
-wn*(-1)*X(15)-Rb*X(11)+2*Rb*X(12)-Rb*X(1)];
% Электромагнитное усилие
F=[(X(2)-X(12))*Ir(1)/(2*tz);
(X(3)-X(1))*Ir(2)/(2*tz);
(X(4)-X(2))*Ir(3)/(2*tz);
(X(5)-X(3))*Ir(4)/(2*tz);
(X(6)-X(4))*Ir(5)/(2*tz);
(X(7)-X(5))*Ir(6)/(2*tz);
(X(8)-X(6))*Ir(7)/(2*tz);
(X(9)-X(7))*Ir(8)/(2*tz);
(X(10)-X(8))*Ir(9)/(2*tz);
(X(11)-X(9))*Ir(10)/(2*tz);
(X(12)-X(10))*Ir(11)/(2*tz);
(X(1)-X(11))*Ir(12)/(2*tz)];
% Скорость
v0=v0+(sum(F)/m)*dt;
end;
% Построение графиков
subplot(2,2,3);
plot(time,s,time,u0p,time,pwm);hold on;
axis([0 0.02 -2.5 2.5]);
subplot(2,2,4);
plot(time,PWM);
axis([0 0.04 -140 140]);
k=0:(K);
subplot(2,2,1); plot(k*dt,v);title('Скорость');
xlabel('t,c');ylabel('v, m/c');grid on
subplot(2,2,2); plot(k*dt,f);title('Электромагнитное усилие');
xlabel('t,c');ylabel('F, H');grid on
end
В таблице 1 приведены идентификаторы, применяемые для математического моделирования системы «АИН ШИМ – АД» в MATLAB, в соответствии с обозначениями, приведенными на функциональной схеме рис. 1.
Таблица 1
Таблица идентификаторов
|
Наименование |
Обозначение на функциональной схеме |
Идентификатор |
|
Сигнал задания в фазах |
s |
|
|
s_2pi3 |
||
|
s_4pi3 |
||
|
Выходные сигналы нуль-органов |
|
pwm |
|
|
pwm_2pi3 |
|
|
|
pwm_4pi3 |
|
|
Импульсные напряжения на обмотках фаз двигателя |
|
PWM |
|
|
PWM_2pi3 |
|
|
|
PWM_4pi3 |
Временные зависимости скорости и электромагнитного усилия асинхронного двигателя при питании от АИН для случаев с амплитудой напряжения питания 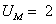и 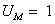приведены на рис. 6 и 7 соответственно.
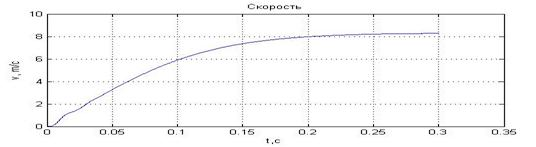
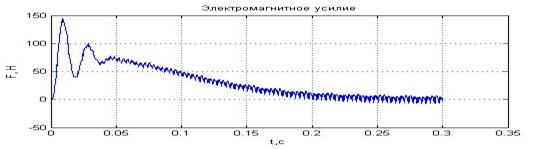
Рис. 6. Результат моделирования системы «АИН ШИМ – АД» при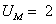
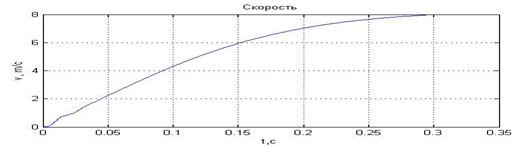
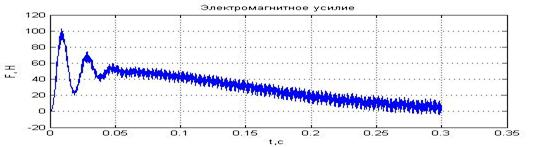
Рис. 7. Результат моделирования системы «АИН ШИМ – АД» при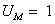
Литература:
1. Емельянов А.А. и др. Моделирование асинхронного двигателя с помощью магнитных и электрических схем замещения / Емельянов А.А., Медведев А.В., Кобзев А.В., Бочкарев Ю.П., Евдокимов О.В. // Молодой ученый. – 2013. - №5. – С. 4-16.
2. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. — Екатеринбург: УРО РАН, 2000. — 654 с.
3. Емельянов А.А. и др. Моделирование системы АИН ШИМ – линейный асинхронный двигатель (Z1 = 6) с обмоткой индуктора через ярмо / Емельянов А.А., Медведев А.В., Кобзев А.В., Козлов А.М., Бесклеткин В.В., Бочкарев Ю.П., Авдеев А.С., Чернов М.В., Габзалилов Э.Ф., Киряков Г.А. // Молодой ученый. – 2013. - №11. – С. 18-28.
