Введение. Решение комбинаторных задач с применением электронных таблиц может служить инструментом для интеграции математического образования с практическими цифровыми навыками, необходимыми в профессиональной и исследовательской деятельности.

Классические комбинаторные задачи могут быть сведены к определенным схемам — сочетаниям, размещениям, перестановкам, где перечисленные выборки — результат отбора некоторого множества объектов из исходного при выполнении определенных условий, и решены с применением формул, соответствующих выбранному типу выборки, а также основных правил комбинаторики (суммы, произведения) и метода включений и исключений.

Эти же задачи могут быть представлены в другой интерпретации: в терминах распределения объектов по классам — раскладки предметов по ящикам.

Владея обеими классификациями, можно легко сориентироваться, к какому типу принадлежит та или иная задача, и, соответственно, решить ее.

Решение задач о раскладке предметов по ящикам сводится к известным схемам с выборками, иногда формула получается более громоздкая, но на этом этапе обучения важным представляется именно умение правильно классифицировать задачу.

Упростить вычисления (получение численного ответа) при решении большого количества задач можно, создав специальный программный продукт [1]. Но можно использовать менее ресурсозатратное средство — Microsoft Excel. Благодаря его наглядности каждый этап вычислений происходит «на глазах», тем самым цепочку логических и вычислительных операций легко проверить и скорректировать. Главным же аргументом в пользу такого выбора стали встроенные комбинаторные функции — ФАКТР, ЧИСЛКОМБ, ПЕРЕСТ, — использование которых позволяет избежать рутинного программирования базовых алгоритмов.

Постановка задачи. Поставим задачу следующим образом: пусть имеется n предметов, которые распределяются по k ящикам. Ящики могут быть различимы или неразличимы, могут допускаться или не допускаться пустые ящики, а также предметы могут быть различимы или нет [2].

Решим эти задачи на основе знакомых нам выборок и схем.

1. Если предметы различимы, ящики различимы, все ящики непусты, то, воспользовавшись формулой включений и исключений, получим, что число способов распределения равно

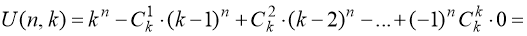
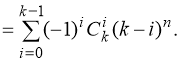
2. Если предметы различимы, ящики различимы, допускаются пустые ящики, получаем в точности известную задачу на размещения с повторениями, число способов распределения равно

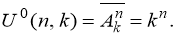
3. Если предметы различимы, ящики неразличимы, все ящики непусты, то имеем задачу, аналогичную первой, но так как порядок ящиков теперь не важен, разделим на число их перестановок, получим, что число способов распределения равно

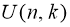
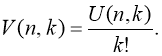
4. Если предметы различимы, ящики неразличимы, допускаются пустые ящики, то можно свести эту задачу к предыдущей, перебрав все возможные числа ящиков — от 1 до k , тогда число способов распределения равно

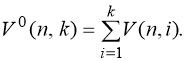
5. Если предметы неразличимы, ящики различимы, все ящики непусты, то можно воспользоваться известной схемой с перегородками, выложим предметы в ряд, между ними имеется
6. n — 1 место, выберем k — 1 позицию для перегородок, тогда число способов распределения равно

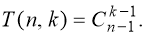
Можно привести другое рассуждение: разложим по одному предмету в ящик, обеспечив выполнение условия непустоты, остальные n — k предметов можно разложить способами.

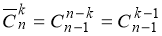
7. Если предметы неразличимы, ящики различимы, допускаются пустые ящики, то имеем классическую задачу на сочетания с повторениями, число способов распределения равно

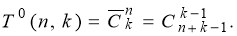
8. Обозначим число способов раскладки неразличимых предметов в неразличимые ящики при условии, что все ящики непусты, , а при допущении пустых ящиков — Выполним условие непустоты, разложим в каждый ящик по одному предмету, тогда оставшиеся можно класть куда угодно, число способов распределения равно

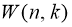
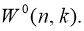
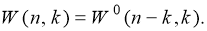
9. Если предметы неразличимы, ящики неразличимы, допускаются пустые ящики, перебрав все возможные числа ящиков, получаем, что число способов распределения равно

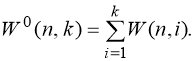
Для двух последних задач явное решение не получено, пара рекурсивных формул позволяет сводить вычисления количества способов распределения при больших значениях n и k к вычислениям с меньшими значениями этих переменных.

Реализация. Перечислим основные используемые функции:

=ЧИСЛОКОМБ(число; число выбранных) — возвращает количество комбинаций для заданного числа элементов без повторений;

=A^B — запись для возведения числа в степень;

=ФАКТР(число) — возвращает факториал числа;

=СУММ(число1; число2; …) — возвращает сумму как отдельные значения, так и целые диапазоны ячеек;

=A1 — ссылка на ячейку, чтобы вернуть значение.

Задача 1. Сколькими способами можно распределить 11 различных открыток в 5 различных конвертов, если все конверты непустые.

Формула в Excel имеет следующий вид:

=ЧИСЛКОМБ(E4;0)*E4^D4 — ЧИСЛКОМБ(E4;1)*(E4–1)^D4 + ЧИСЛКОМБ(E4;2)*(E4–2)^D4 — ЧИСЛКОМБ(E4;3)*(E4–3)^D4 + ЧИСЛКОМБ(E4;4)*(E4–4)^D4 — ЧИСЛКОМБ(E4;5)*(E4–5)^D4.

Значения, которые используются в формуле =ЧИСЛОКОМБ «подтягиваются» из соответствующих столбцов, заполненных согласно условию.

Для заданных исходных данных получаем ответ 29607600.

Задача 2. Сколькими способами можно распределить 11 различных открыток в 5 различных конвертов, если допускаются пустые конверты.

Формула в Excel имеет следующий вид: =E4^D4.

Аналогично с задачей 1 используются значения из соответствующего столбца и используется функция подсчёта числа в степени.

Для заданных исходных данных получаем ответ 48828125.

Задача 3. Сколькими способами можно распределить 11 неразличимых открыток в 5 различных конвертов, если все конверты непустые.

Формула в Excel имеет следующий вид: =F4 / ФАКТР(E4).

Так как в формуле используется значение, полученное в пункте 1, добавляем ссылку на это значение и делим на факториал числа k .

Для заданных исходных данных получаем ответ 246730.

Задача 4. Сколькими способами можно распределить 11 неразличимых открыток в 5 различных конвертов, если допускаются пустые конверты.

В формуле используется сумма V ( n , i ), чтобы найти все значения, создаем вспомогательную таблицу для подсчета всех значений. Далее, найдя все значения, используем функцию =СУММ, чтобы найти ответ на поставленную задачу.

= СУММ(H4:L4)

= 1

= (2^D4 — ЧИСЛКОМБ(2;1)*1^D4)/ФАКТР(2)

= (3^D4 — ЧИСЛКОМБ(3;1)*2^D4 + ЧИСЛКОМБ(3;2)*1^D4)/ФАКТР(3)

= (4^D4 — ЧИСЛКОМБ(4;1)*3^D4 + ЧИСЛКОМБ(4;2)*2^D4 — ЧИСЛКОМБ(4;3)*1^D4)/ФАКТР(4)

= =(5^D4 — ЧИСЛКОМБ(E4;1)*4^D4 + ЧИСЛКОМБ(E4;2)*3^D4 — ЧИСЛКОМБ(E4;3)*2^D4 + ЧИСЛКОМБ(E4;4)*1^D4)/ФАКТР(E4)

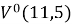
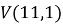
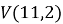
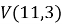
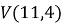
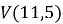
Продолжаем, сколько это требуется в соответствии с условием задачи. Ответ и промежуточные результаты представлены на рисунке 1.

Рис. 1. Расчеты для задачи 4

Задача 5. Сколькими способами можно представить число 11 (11 неразличимых единиц) в виде 5 положительных целых слагаемых (пустые ящики не допускаются), если представления, отличающиеся только порядком слагаемых, считаются одинаковыми.

Формула в Excel имеет следующий вид: =ЧИСЛКОМБ(D5–1;E5–1).

Аналогично с предыдущими задачами используем значения из соответствующего столбца и используем функцию подсчёта числа комбинаций. Получаем ответ: 210

Задача 6. Сколькими способами можно представить число 11 (11 неразличимых единиц) в виде 5 неотрицательных целых слагаемых (пустые ящики допускаются), если представления, отличающиеся только порядком слагаемых, считаются различными.

Формула в Excel имеет следующий вид: =ЧИСЛКОМБ(D5+E5–1;E5–1).

Получаем ответ: 1365

Задачи 7–8. Сколькими способами можно представить число 11 в виде 5 положительных / неотрицательных целых слагаемых, если представления, отличающиеся только порядком слагаемых, считаются одинаковыми.

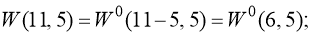
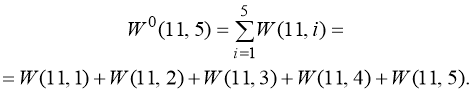
Так как фактически имеем систему двух рекуррентных соотношений, создаем вспомогательную рекурсивную таблицу, которую заполняем, используя ссылки на соответствующие элементы для поиска текущих значений. После заполнения таблицы отбираем ответы под условия задачи. Рабочая таблица представлена на рисунке 2.

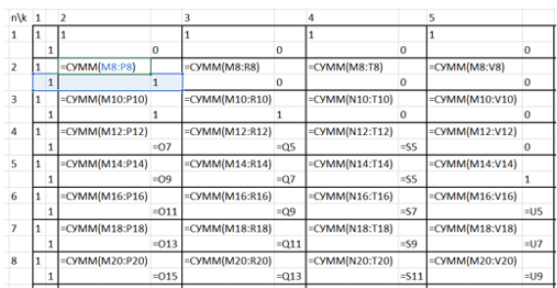
Рис. 2. Расчеты для задач 7–8

Таким образом, получена таблица, в которой в верхнем левом углу каждой ячейки имеется значение , а в правом нижнем углу —соответствующее значение . Итоговая таблица представлена на рисунке 3.

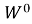
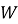
Рис. 3. Результаты для задач 7–8

Ответы на обе задачи находим в соответствующей ячейке: 37 и 10.

Выводы. Таким образом, Excel может послужить хорошим дидактическим инструментом в процессе освоения комбинаторики. Он позволяет быстро прототипировать решение, переводя задачу в наглядную табличную модель, которую легко корректировать. Преобразование реальной проблемы в структурированную табличную модель — важное умение для будущего специалиста, ведь зачастую Excel выступает основным рабочим инструментом. Процесс построения решения в Excel требует декомпозиции задачи на элементарные шаги (формулы, условия, ссылки), что тренирует алгоритмическое решение. Видеть данные в системе, выстраивать логические цепочки и предвидеть результат вычислений — важный практический навык. На стыке дискретной математики, математической логики и цифровой грамотности формируется гибридный набор компетенций.

Литература:

1. Голик А. А., Сухан И. В. Разработка программного обеспечения для эффективного решения комбинаторных задач. В сборнике: Теоретические и прикладные аспекты естественно-научного образования в эпоху цифровизации. Материалы IV Международной научно-практической конференции. В 2-х томах. Брянск, 2025. С. 58–64.
2. Тишин В. В. Дискретная математика в примерах и задачах. — СПб.: БХВ-Петербург, 2008.