Подгрупповые функторы, представляющие собой функции, согласованные с изоморфизмами групп и выделяющие в них системы подгрупп, изначально возникли в теории радикалов колец. В теории конечных групп они применялись для обобщения конкретных теоретико-групповых объектов, аксиоматизируя их ключевые свойства. Систематическое изучение подгрупповых функторов началось в начале XX века (см., например, [1, 2]). Позднее было показано, что подгрупповые функторы являются удобным инструментом для изучения классов групп. Значительный вклад в развитие теории подгрупповых функторов внесли С. Ф. Каморников, А. Н. Скиба, М. В. Селькин и другие алгебраисты (см., например, [3–6]). Обзор основных результатов в этой области, классификация подгрупповых функторов и разработанные связи подгрупповых функторов с различными классами групп представлены в монографии [5].
Рассматриваются только конечные группы. Обозначения и определения, используемые в статье, являются стандартными (см., например, [5, 7]). Приведем лишь некоторые из них. Через

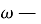
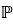
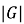


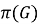


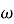

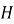

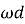

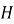
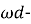
Классом групп
называется всякая совокупность групп, которая с каждой своей группой содержит и все группы, ей изоморфные [7, с. 161]. Через
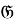

Определение 1.
Отображение
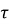

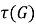
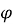

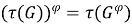
Подгруппа группы

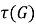
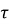

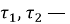
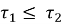


Определение 2.
Следуя [5, с. 14], подгрупповой функтор
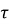
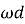

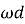
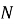
-
из того, что
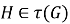
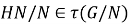
-
из того, что
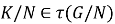
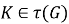
Определение 3
. Следуя [5, с. 16], подгрупповой функтор
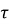
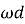

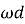
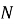
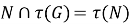

Определение 4.
Следуя [5, с. 15], подгрупповой функтор
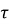
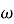

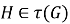
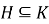
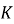

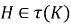
Замечание 1.
В случае, когда
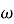

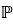
Определение 5.
Пусть
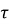
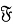
—
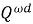
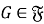
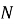
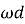

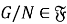
—
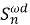
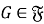
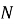
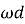

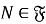
—
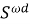
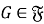
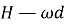

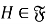
Через

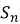
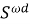
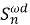

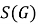

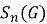

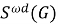
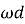

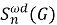
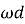

В работе [3] для подгруппового функтора
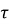

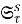
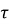
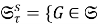
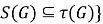
Следуя [3], для произвольного подгруппового функтора
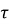
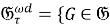
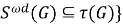
В теореме 1 установлены свойства подгруппового функтора
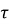
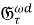
Теорема 1.
Пусть
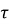
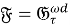
-
Если
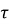
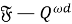
-
Если
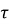
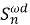
-
Если
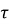
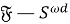
Доказательство.
1. Пусть
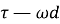
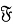
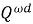
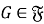
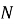
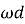

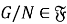
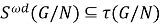
Пусть
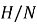
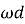
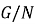


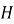
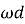

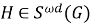
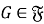
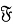
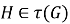
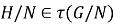
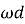
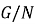
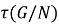
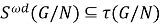
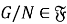
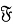
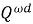
2. Пусть
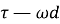
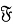
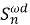
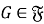
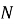
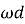

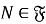
Пусть
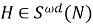
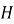
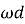
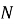
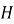
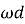

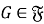
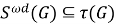
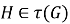

т. е.
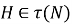
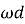
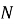

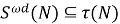
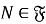
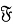
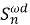
3. Пусть
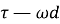
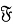
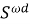
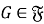
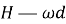

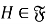
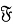
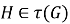
Рассмотрим произвольную подгруппу
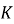
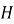
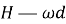

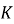
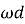

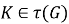
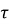
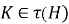
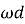
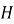
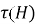
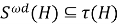
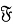
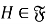
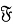
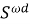
Теорема доказана.
Замечание 2.
В случае, когда
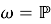
Литература:
- Amitsur S. A. General Theory of Radicals // Amer. J. Math. — 1952. — V. 74. — P. 774–786.
- Amitsur S. A. General Theory of Radicals // Amer. J. Math. — 1954. — V. 76. — P. 100–136.
- Каморников С. Ф. Включающие подгрупповые функторы // Сибирский математический журнал. — 2015. — Т. 56. — С. 1057–1067.
- Каморников С. Ф. Радикальные дистрибутивные функторы // Математические заметки. — 2000. — Т. 68. — № 1. — С. 91–97.
- Каморников С. Ф., Селькин М. В. Подгрупповые функторы и классы конечных групп. — Минск: Беларуская навука. — 2003. — 254 с.
- Скиба А. Н. Алгебра формаций. — Минск: Беларуская навука. — 1997. — 240 с.
- Монахов В. С. Введение в теорию конечных групп и их классов. ‒ Минск: Вышэйшая школа, 2006. ‒ 207 с.
- Шеметков Л. А. Формации конечных групп. ‒ М.: Наука, 1978. — 272 с.

