В статье предложена методика для описания двухфазных смесей — суспензий, взвеси кристаллических частиц в насыщенном растворе. Расчетная область рассматривается в виде U-образного сосуда, в нисходящей ветви которой поддерживается постоянный уровень, а в восходящей ветви производится подвод тепла, испарение и кристаллизация. Проведено сравнение с другим случаем процесса кристаллизации, когда образование твердой фазы происходит на стенках аппарата либо формируется слой отложений на дне.
Ключевые слова: раствор, твердая фаза, кристаллизация, суспензия.
При расчете процессов кристаллизации в выпарных аппаратах-кристаллизаторах возникает задача определения состава двухфазной смеси — твердой фазы и насыщенного раствора. Этот вопрос особенно актуален в химических технологиях [1, 2].
В ряде случаев для получения твердой фазы из раствора используются U?образные сообщающиеся сосуды, в одну из частей которых производится подача раствора с малой концентрацией растворенного вещества, а во второй половине в результате подвода тепла происходит увеличение концентрации и образование твердой фазы. В обычном расчете выполняются тепловой и массовый балансы, с помощью которых определяют количество образующейся твердой фазы.
Ранее [3] были получены соотношения для описания двухфазной смеси в выпарном аппарате-кристаллизаторе для случая, когда кристаллизация происходит на поверхностях нагрева и стенках восходящей ветви (для краткости — «модель осаждения») либо осаждается на дне.
Свойства веществ могут значительно различаться, а поэтому на описание процесса образования двухфазной смеси — суспензии,- следует обратить внимание. Далее именуем эту модель — «суспензия».
Пусть поперечное сечение восходящей ветви кристаллизатора постоянно. Это условие позволяет получить простые соотношения для восходящей ветви, где происходит процесс кристаллизации и образуется суспензия. Пусть будут известны в нисходящей ветви следующие фиксированные величины: плотность раствора ρd и фиксированное значение уровня hd. Допустим, что в некоторый момент времени в восходящей ветви известны: суммарная масса растворенного вещества в суспензии (как в растворе, так и во взвеси) ![]() , концентрация насыщенного раствора с’ (на единицу массы раствора), плотность раствора
, концентрация насыщенного раствора с’ (на единицу массы раствора), плотность раствора ![]() при с’, плотность твердой фазы
при с’, плотность твердой фазы ![]() , площадь поперечного сечения Fup. Находим суммарную массу суспензии для восходящей ветви:
, площадь поперечного сечения Fup. Находим суммарную массу суспензии для восходящей ветви:
hd·ρd = hup·![]() ,
, ![]() · hup·
· hup·![]() .
.
Масса растворителя в восходящей ветви теперь может быть определена:
![]() .
.
Массу раствора для восходящей ветви получаем из соотношения:
![]() .
.
Вычисляем массу твердой фазы в восходящей ветви аппарата:
![]()
Объемы для компонентов в восходящей ветви вычисляем следующим образом:
![]() ,
, ![]() ,
,
![]() .
.
Определяем высоту уровня суспензии в подъемной ветви, объемное и массовое содержание твердой фазы в смеси:
hup = ![]() /Fup, α=
/Fup, α= ![]() , x=
, x= ![]() .
.
Новизна — возможность отслеживания динамики свойств суспензии в условиях кристаллизации с привлечением минимума данных. Особенно важно для аварийных, «нерасчетных» режимов эксплуатации кристаллизатора. Для процессов снижения/наброса температуры в химических аппаратах, которые приводят к изменению фазового состава смеси, данные оценки также пригодны.
Теперь следует обратить внимание на сравнение изложенной модели двухфазной смеси «суспензии» с «моделью осаждения» [3], когда рассматривается модель двухфазной смеси — насыщенный раствор/отложения на стенках либо на дне аппарата. В общем случае выбор модели определяется физико-химическими свойствами компонентов смеси. Также обязательным является учет особенностей физического процесса. Например, длительность рассматриваемого процесса должна верно соотноситься со скоростью осаждения частиц в суспензии, подводимая тепловая мощность должна учитывать соотношения между высотными отметками поверхности нагрева и уровнем смеси, толщина отложений на поверхности нагрева влияет на подводимое количество тепла и т. п.
Тем не менее, произведем сравнение результатов двух методик на одной из солей — для «суспензии» и «модели осаждения». Еще раз следует напомнить, что при этом игнорировались многие физико-химические свойства соли, влияющие на конкретные физические процессы при образовании твердой фазы. Учитывались исключительно следующие свойства: плотность твердой и жидкой фаз, параметры насыщенного раствора.
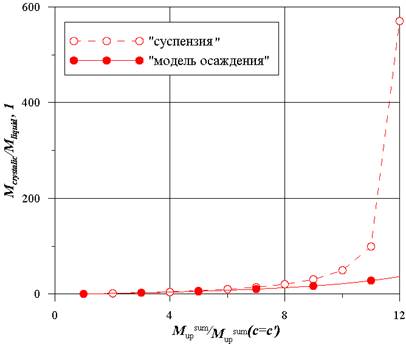
Рис. 1. Относительная масса твердой фазы
На рисунках 1?4 в сравнении представлены основные результаты расчета для обоих моделей. Завышенные, редко встречающиеся в химических технологиях, параметры на оси абсцисс могут соответствовать исключительно аварийным режимам работы аппарата. Кроме того, они позволяют наглядно продемонстрировать отличие моделей. Различие в результатах обусловлено разницей в плотности двухфазной смеси, заполняющей восходящую ветвь устройства. Для «модели осаждения» плотность раствора неизменна, соответствует параметрам насыщения, изменяется лишь объем, занятый жидкой фазой из-за выпадения кристаллов. Для «суспензии» плотность смеси определяется как плотностью насыщенного раствора, плотностью твердой фазы, а также ее массовым содержанием.
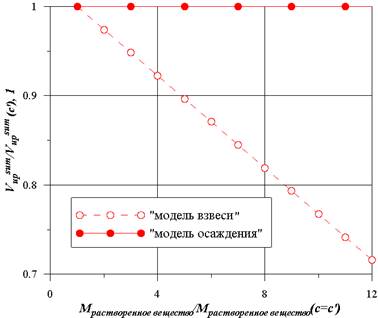
Рис. 2. Объем смеси в подъемной ветви
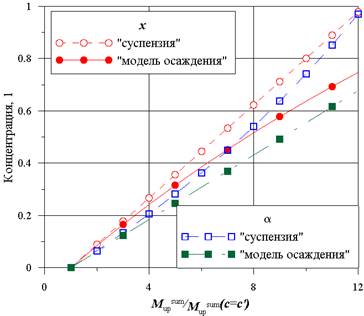
Рис. 3. Концентрация твердой фазы
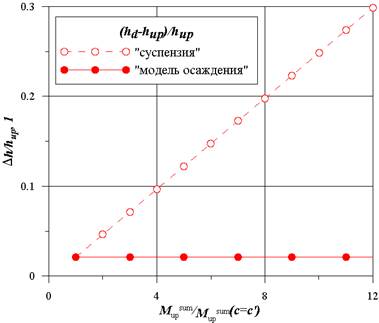
Рис. 4. Положение уровня в восходящей ветви
Существенное различие результатов, с точки зрения работоспособности аппарата, для перечисленных моделей — изменение объема и уровня смеси, которыми нельзя пренебрегать при описании аварийных режимов с отклонениями от номинальных параметров. В этом случае важными становятся высотные отметки поверхности нагрева, уровня суспензии в устройстве, количество жидкой фазы.
В ряде индустриальных технологий возникают очень близкие проблемы, например, в ядерной энергетике [3], где затрагивался вопрос о возможности повышения концентрации и образования твердой фазы из насыщенного раствора при длительном кипении теплоносителя в активной зоне. Все изложенное может найти применение в этом случае.
Литература:
1. Касаткин А. Г. Основные процессы и аппараты химической технологии. М.: Госхимиздат, 1961, 830 с.
2. Гельперин Н. И. Основные процессы и аппараты химической технологии. М.: «Химия», 1981, 812 с.
3. Шмаль И. И. Аналитические оценки для процесса кристаллизации // Молодой ученый. — 2013. — № 7. — С. 30?31.
4. Логвинов С. А., Безруков Ю. А., Драгунов Ю. Г. Экспериментальное обоснование теплогидравлической надежности реакторов ВВЭР. М.: ИКЦ «Академкнига», 2004, 255 с.

