Цель: обобщение и закрепление знаний закрепление и систематизация полученных знаний за учебный год.
Задачи:
Образовательные:
- Закрепить навыки количественного и порядкового счета, соотнесение цифр с количеством и порядком предметов.
- Закрепить навыки ориентировки в пространстве, координации речи с движениями.
- Упражнять в правильном употреблении предлогов в речи и составлении предложений с ними.
Развивающие:
- Развивать слуховое внимание, память, мышление.
- Активизировать речевую деятельность, самоконтроль речи.
Воспитательные:
- Формировать положительную мотивацию на занятии.
- Воспитывать умение слушать и понимать устную речь.
- Воспитывать стремление достигать поставленной цели.
- Воспитывать навыки коллективного сотрудничества и взаимопонимания.
Оборудование: воздушные шары, предметные картинки, схемы предлогов, разрезные картинки, презентация.
Ход занятия
Логопед: Какой прекрасный весенний день сегодня. Посмотрите, как ярко засветило солнце от ваших улыбок.
Протянуло солнышко нам свои ладошки,
Позвало нас солнышко к сказочным дорожкам.
Логопед: Солнышко предлагает проснуться и сделать массаж лица.
Солнышко проснулось, (сжимать пальцы в кулачки и разжимать их).
Лобика коснулось, (проводить пальчиками обеих рук по лбу).
Лучиками провело и погладило, и погладило. (проводить пальчиками обоих рук по лбу).
Солнышко проснулось, (сжимать пальцы в кулачки и разжимать их).
К щечкам прикоснулось, (проводить пальчиками обоих рук по щекам).
Лучиками провело и погладило, и погладило. (проводить пальчиками обеих рук от носа к средней части ушей).
Солнце личико согрело, потеплело, потеплело. (ладонями греем лицо)
Наши ручки потянулись, наши губки улыбнулись. (потянуться руками вверх, улыбнуться)
Логопед: Сегодня солнышко пригласило нас к сказочной дорожке. Чтобы отправиться в путешествие и узнать в какую сказку мы попадем, необходимо отгадать героя этой сказки.
Он носит вместо шапки
Веселый колпачок.
И ростом он всего лишь
С ребячий башмачок.
С фонариком и с песней
Идет в лесу ночном…
Не ошибешься, если
Ты скажешь: это … (гном)
Логопед: Ребята, а в какой сказке встречаются гномы? Сегодня мы отправимся в сказку Белоснежка и семь гномов. Закрывайте глаза.
В сказке может все случиться,
Наша сказка впереди,
Сказка в двери к нам стучится
Скажем: сказка заходи.
(звучит музыка, выходит гном с воздушными шарами, на шарах цифры и задания)
Гном: Здравствуйте, ребята, меня зовут Гном Весельчак. Я пришел к вам из сказки Белоснежка и семь гномов. Белоснежкой съела отравленное яблоко и уснула крепким сном. В нашей сказке все пошло не так, принц не смог разбудить Белоснежку. Злая колдунья сказала, что Белоснежка откроет глаза, когда мы сможем выполнить трудные и сложные задания. Задание обозначены цифрами на этих воздушных шарах. Колдунья требует выполнить задания не по порядку, а от обратного счета. А мы знаем только порядковый счет. Без вашей помощи нам не справится!
Логопед: Ребята, давайте поможем гномам!
Гном: Чтобы превратиться в моих братьев гномов и помочь выполнить трудные задания нужно надеть на себя эти волшебные колпаки. (одеваем детям на голову колпаки, звучит музыка)
Задание № 7 «Подбери схемы предлогов к картинкам».
Логопед: Приступим к выполнению задания. С какой цифры мы начнем, если нужно выполнять задания от обратного? Начинаем задание с цифры 7 . Вам необходимо подобрать картинку и нужную схему предлога, составьте предложение по картинке.








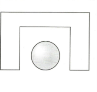

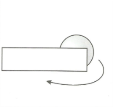
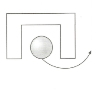
Логопед: Посмотрите на экран, цифра 7 исчезла, значит задание мы выполнили правильно. (презентация)
Задание № 6 «Нелепицы»
Логопед: Ребята, а теперь посмотрите на экран. Найдите ошибки у художника, используйте в ответах маленькие словечки — предлоги.

Гном: Вот и цифра 6 исчезла, значит задание выполнили верно. (презентация)
Задание № 5 «Собери картинку».
Логопед: Ваша задача составить предложение по схемам.

Логопед: Обратите внимание ребята, не стало цифры 5. (презентация)
Задание № 4 «Расставь предметы»
Логопед: Приступим к следующему заданию. Каждому из вас я раздам картинку. Ваша задача в правильном порядке расставить предметы на магнитной доске. Слушайте внимательно! В центре стоит дом. (ставит педагог)
- За домом растет дерево.
- Над домом плывут облака.
- За облаками светит солнце.
- На крыше сидит ворона.
- В будке спит собака.
- Из-за куста выглядывает кот.
- Из-под крыльца смотрит мышь.
Логопед: Вот и цифра 4 пропала на экране. Значит мы на верном пути, скоро мы разбудим Белоснежку. (презентация)
Логопед: Предлагаю перед следующим сложным заданием отдохнуть, набраться сил. Повторяйте вместе со мной.
Динамическая пауза.
Дом у гномика лесной
И стоит он под сосной.
Утром выйдет гном из дома –
Все вокруг ему знакомо.
На сосне сидит сова,
Под сосной растет трава.
Слева — кустики черники.
Справа — кустик земляники.
Очень любит милый гном
Свой лесной уютный дом.
Ну а мы продолжим путь
Гному нужно отдохнуть.
Задание № 3 «Задачки»
Гном: Колдунья предлагает решить задачки. Слушайте внимательно.
- Мышки кошки испугались,
По углам все разбежались.
1 — в ящик,
12 — за ней.
Сколько было всех мышей? (13)
- Ежик по лесу пошел,
На обед грибы нашел:
5 под березой,
6 под осиной.
Сколько их будет в плетеной корзине? (11)
- На кустике перед забором
12 ярко красных помидоров.
Потом 2 оторвалось
И сколько на кусте осталось? (10)
- Что так начало греметь?
Ульи строит наш медведь.
Ульев сделал он лишь 7
На 2 меньше, чем хотел.
Сколько ульев хотел сделать Мишка? (9)
- Ежик по грибы пошел
14 рыжиков нашел.
7 грибов в корзинку,
Остальные на спинку.
Сколько рыжиков везешь
На своих иголках еж? (7)
Логопед: Посмотрите на экран, а вот и цифра 3 исчезла (презентация)
Задание № 2 Математические примеры
Гном: Ох, и трудные примеры приготовила колдунья. Мы попробовали с гномами их решить, но совершили ошибки. Помогите нам исправить ошибки.

Логопед: Не стало цифры 2. Вы отлично справились с заданием! (презентация)
Задание № 1 Подарок для колдуньи — открытка букет
Гном: Здесь в этом конверте одни осколки, что же задумала колдунья. (в конверте разрезная картинка — ваза). Давайте попробуем сложить их.
Гном: Смотрите — это же ваза! Не красиво возвращать пустую вазу, предлагаю наполнить эту вазу цветами, может быть тогда колдунья станет добрее к нам и снимет свои чары с Белоснежки.
Логопед: Очень хорошо ты придумал гном. Мы сможем с ребятами сделать цветы из красивой бумаги (аппликация).
Гном: Ура! Последняя цифра пропала. Посмотрите! Вот Белоснежка и проснулась! (презентация)
Логопед : Благодаря такому чудесному подарку злая колдунья пообещала больше не менять сказку! Мы с вами помогли гномам справиться со всеми заданиями. Заклятье снято, и наша Белоснежка проснулась! (презентация)
Гном: Спасибо за помощь! Я всегда буду рад вас видеть в своей сказке. До новых встреч!
Логопед: Ребята, а какое задание от колдуньи было самым интересным? А самым трудным? Давайте скажем гному спасибо за интересное путешествие и попрощаемся с ним. А нам пора возвращаться в детский сад.
Скажем сказке «До свидания!»
И спасибо скажем ей,
Пусть большое расстоянье
Нам не даст забыть друзей.
Логопед: На этом наше путешествие завершилось. Спасибо за хорошую работу!







