Постановка задачи обнаружения и измерительная модель RM

Рассмотрена постановка задачи обнаружения протяженного объекта с использованием лидара. Приведена измерительная модель на основе случайной матрицы.

Ключевые слова: протяженный объект, случайная матрица, лидар.

Модель случайной матрицы (RM) — это типичный метод моделирования протяженных объектов, который широко используется при обнаружении и отслеживании названных объектов. Однако существующие системы и устройства на основе модели RM обычно предполагают, что измерения следуют по гауссову распределению, что, в свою очередь, может привести к снижению точности при применении устройства в лидарной системе. Была предложена новая модель обнаружения, используемая для модификации устройства на основе модели RM с учетом характеристик 2D-данных лидара.

Предлагаемый метод отличается от описанного в [1] и не предполагает большого количества излишних измерений. Нами в достаточном объеме рассмотрены характеристики обнаружения лидарной системы на основе реальных данных лидара. Таким образом, предлагаемый метод позволяет лучше оценить кинематику и протяженность обнаруживаемого объекта. Следует обратить внимание на то, что предлагаемый метод может использоваться только для обнаружения и отслеживания одного протяженного объекта, а не является системой для обнаружения и отслеживания нескольких объектов.

Для разработки предлагаемого метода рассмотрим сначала постановку задачи обнаружения на основе модели RM.

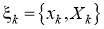
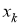
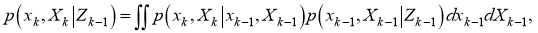
Пусть  _k обозначает размер объекта (или состояние протяженности) в момент времени k . Модель RM обычно определяется следующим выражением: , где — кинематический вектор; X _k — матрица d × d , используемая для описания размера протяженного объекта; d — размерность пространства отслеживания. Используя структуру байесовской фильтрации, предсказание состояния опишется так:

(1)

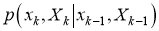
Уточнение состояния записывается следующим образом:

(2)

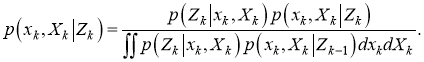
Модель RM предполагает, что x _k соответствует распределению Гаусса, а X _k соответствует обратному распределению Уишарта. Следовательно, согласно [2], плотность состояний объекта на основе факторизованной модели равна:

(3)

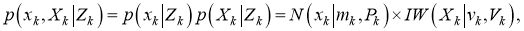
где N (·) обозначает распределение Гаусса, а IW (·) обозначает обратное распределение Уишарта.

В исходной модели случайной матрицы для набора измерений обычно предполагается, что каждый

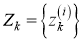
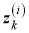
Однако в 2D-лидарной системе измерения распределены по контуру объекта и может быть обнаружена только одна сторона (в данном случае автомобилем). Среднее значение и ковариация Z _k не могут точно описать реальное положение или размеры объекта. Следовательно, проблема модели RM заключается в том, что она не может оценить реальное состояние объекта, когда данные поступают из 2D-лидарной системы.

Перейдем далее к рассмотрению измерительной модели 2D-лидара, которая понадобится нам в дальнейшем.

Необработанные данные лидара обычно имеют полярный формат, например , где и обозначает расстояние и радиан i-го диапазона за обзор соответственно.

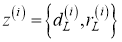
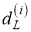
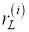
В соответствии с принципом обнаружения лидара при его применении в реальных условиях были сделаны следующие предположения:

1. Лидар осуществляет обнаружение раз за один обзор, а i радиан наблюдения r ^{( i )} следует из распределения Гаусса , где — заданная дисперсия;
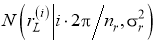
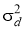
2. Диапазон шума соответствует распределению Гаусса с нулевым средним значением с дисперсией ;
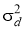
3. В зависимости от различных факторов помех, таких как погода или сильный свет, вероятность обнаружения объекта равна ;
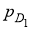
4. Если объект может быть обнаружен по различию материала его поверхности, то вероятность обнаружения каждого диапазона равна .

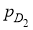
На основании вышеизложенных предположений модель измерения можно описать следующим образом:

1. Пусть обозначает набор измерений за один обзор. Согласно предположению 3 существует вероятность того, что Z представляет собой пустое множество;
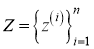
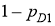
2. Когда Z не является пустым множеством, согласно предположению 4, существует вероятность , что z ^{( i )} также представляет собой пустое множество;
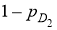
3. Пусть и обозначают положения лидара и объекта согласно предположениям 1 и 2, где и определяются следующим образом:

(4а)

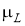
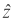
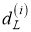
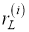
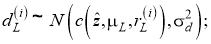
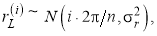
где с (.) обозначает обнаруживаемую контурную функцию объекта.

Например, — результат ранжирования объекта с центральной координатой z . Координаты лидара — , радиан обнаружения — .

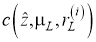
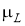
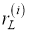
Хотя в некоторых методах слежения на основе RM также обсуждается проблема слежения в лидарной системе, результаты слежения должны рассчитываться в соответствии с характеристиками конкретных объектов. Например, в [3] использовалась такая информация, как направление движения вперед и угол поворота передних колес; таким образом, метод подходит только для отслеживания транспортных средств прямоугольной формы. Предложенный метод предлагает еще одну интересную идею — возможность в полной мере использовать измерительные характеристики лидарной системы для оценки реального состояния объекта.

Литература:

1. Hoher, P. et al. Extended target tracking with a lidar sensor using random matrices and a virtual measurement model. IEEE Trans. Signal Process. 70 , 228–239 (2022).
2. Feldmann, M., Frдnken, D. & Koch, W. Tracking of extended objects and group targets using random matrices. IEEE Trans. Signal Process. 59 (4), 1409–1420 (2011).
3. K. Granstrцm, S. Reuter, D. Meissner and A. Scheel, A multiple model PHD approach to tracking of cars under an assumed rectangular shape. Proc. of the 17th International Conference on Information Fusion (FUSION), Salamanca, Spain, pp. 1–8, (2014).