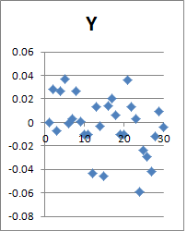
В статье приведен исходный статистический ряд результатов имитационного моделирования, описана методика определения бракованных результатов и рассчитано математическое ожидание, а также среднеквадратическое отклонение выверенного статистического ряда.
Ключевые слова:РК-3 профиль, имитационное моделирование
Процесс сборки РК-3 профильного конического соединения реализован с применением авторского программного обеспечения (рис. 1), которое способно смоделировать процесс движения шероховатого вала с конической поверхностью в трехмерном пространстве с учетом линейных и угловых параметров движения.
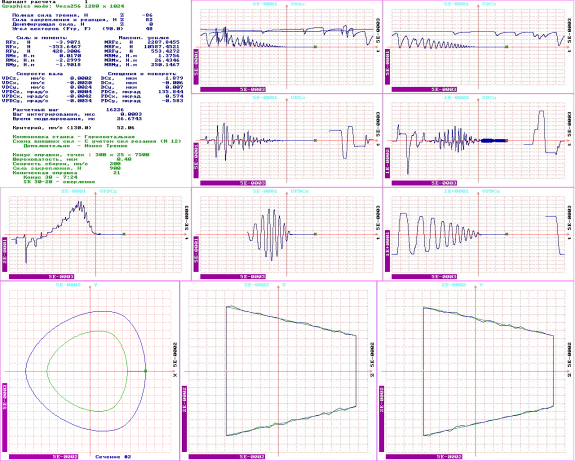
Рис. 1. Моделирование процесса сопряжения РК-3 профильных поверхностей
На основе законов Ньютона выполняется многократное численное моделирование движения с определением ускорений, скоростей и смещений, которые для разных имитационных реализаций (за счет шероховатости поверхности вала) будут приводить к различному конечному закрепленному положению вала в отверстии втулки [1–4].
Таким образом, повторение большого количества реализаций процесса сопряжение деталей конического РК-3 профильного соединения приведет к формированию статистического ряда положения вала, закрепленного в отверстии втулки (табл.1).
Таблица 1
Параметры собранного РК-3 профильного соединения
|
N |
Z |
X |
Y |
Pz |
Px |
Py |
Sf/Sn |
SrZ |
SrN |
SrP |
MaxP |
|
1 |
18.92 |
0.04 |
0.00 |
-1.47 |
-0.07 |
-0.78 |
21.12 |
-0.19 |
0.58 |
0.76 |
7.88 |
|
2 |
35.71 |
-0.01 |
0.00 |
0.27 |
-0.25 |
0.35 |
45.51 |
-0.08 |
0.92 |
2.33 |
10.60 |
|
3 |
36.97 |
0.00 |
0.03 |
-0.64 |
0.50 |
0.02 |
49.07 |
-0.07 |
0.96 |
2.60 |
10.49 |
|
4 |
18.14 |
-0.01 |
0.02 |
0.68 |
0.10 |
0.28 |
21.11 |
-0.18 |
0.58 |
0.76 |
8.25 |
|
5 |
36.85 |
-0.03 |
-0.01 |
-0.52 |
-0.19 |
0.09 |
48.41 |
-0.09 |
0.96 |
2.56 |
10.20 |
|
6 |
37.52 |
0.03 |
0.03 |
2.59 |
0.23 |
-0.59 |
48.90 |
-0.06 |
0.96 |
2.59 |
10.94 |
|
7 |
37.49 |
0.01 |
0.04 |
-1.89 |
0.98 |
0.11 |
48.72 |
-0.07 |
0.96 |
2.58 |
10.50 |
|
8 |
37.20 |
0.00 |
0.00 |
-1.88 |
-0.36 |
-0.07 |
49.12 |
-0.08 |
0.97 |
2.60 |
9.78 |
|
9 |
35.39 |
0.02 |
0.00 |
1.45 |
-0.37 |
-0.39 |
45.72 |
-0.08 |
0.92 |
2.34 |
10.45 |
|
10 |
35.29 |
0.01 |
0.03 |
1.19 |
0.94 |
-0.41 |
45.70 |
-0.07 |
0.93 |
2.33 |
10.21 |
|
11 |
37.24 |
0.00 |
0.00 |
-0.54 |
0.32 |
-0.06 |
49.11 |
-0.08 |
0.97 |
2.60 |
9.94 |
|
12 |
18.77 |
0.02 |
-0.01 |
0.76 |
-0.20 |
-0.28 |
21.08 |
-0.20 |
0.58 |
0.77 |
7.72 |
|
13 |
37.03 |
-0.07 |
-0.01 |
-0.24 |
0.32 |
1.86 |
48.87 |
-0.07 |
0.96 |
2.59 |
9.93 |
|
14 |
37.48 |
0.01 |
-0.01 |
0.38 |
0.17 |
0.02 |
49.07 |
-0.08 |
0.96 |
2.60 |
9.92 |
|
15 |
35.15 |
-0.01 |
-0.04 |
0.30 |
-0.81 |
0.03 |
45.78 |
-0.09 |
0.92 |
2.34 |
9.84 |
|
16 |
37.29 |
0.01 |
0.01 |
-0.67 |
0.44 |
-0.42 |
49.14 |
-0.06 |
0.96 |
2.60 |
9.85 |
|
17 |
37.43 |
-0.01 |
0.00 |
-0.01 |
0.20 |
0.45 |
48.91 |
-0.07 |
0.96 |
2.59 |
9.91 |
|
18 |
35.85 |
0.00 |
-0.05 |
0.05 |
-0.82 |
0.31 |
45.81 |
-0.07 |
0.92 |
2.34 |
9.69 |
|
19 |
37.50 |
-0.02 |
0.01 |
-0.12 |
0.74 |
0.41 |
49.31 |
-0.08 |
0.97 |
2.61 |
9.77 |
|
20 |
37.22 |
-0.03 |
0.02 |
-0.69 |
-0.08 |
0.47 |
48.85 |
-0.07 |
0.96 |
2.58 |
10.65 |
|
21 |
18.46 |
0.04 |
-0.01 |
-2.10 |
0.02 |
-0.86 |
21.09 |
-0.19 |
0.58 |
0.77 |
7.86 |
|
22 |
37.07 |
-0.01 |
0.01 |
2.18 |
0.12 |
0.19 |
48.95 |
-0.06 |
0.97 |
2.60 |
9.75 |
|
23 |
18.57 |
-0.03 |
-0.02 |
0.29 |
-0.15 |
0.52 |
21.05 |
-0.20 |
0.58 |
0.76 |
7.61 |
|
24 |
35.36 |
-0.05 |
-0.01 |
6.14 |
0.09 |
0.45 |
45.56 |
-0.08 |
0.92 |
2.33 |
9.62 |
|
25 |
18.37 |
0.06 |
-0.01 |
-2.61 |
0.08 |
-1.43 |
21.22 |
-0.19 |
0.58 |
0.77 |
8.14 |
|
26 |
18.55 |
0.02 |
0.03 |
1.70 |
0.28 |
-0.36 |
21.00 |
-0.19 |
0.58 |
0.76 |
8.39 |
|
27 |
37.14 |
0.03 |
-0.01 |
0.69 |
-0.46 |
-0.43 |
48.75 |
-0.08 |
0.96 |
2.58 |
10.89 |
|
28 |
18.92 |
0.00 |
0.00 |
1.34 |
-0.01 |
0.11 |
21.07 |
-0.19 |
0.57 |
0.77 |
7.97 |
|
29 |
35.32 |
-0.01 |
0.04 |
-1.71 |
1.05 |
0.37 |
45.50 |
-0.09 |
0.92 |
2.33 |
9.97 |
|
30 |
37.22 |
-0.02 |
0.01 |
2.01 |
0.20 |
0.20 |
48.80 |
-0.07 |
0.96 |
2.58 |
11.04 |
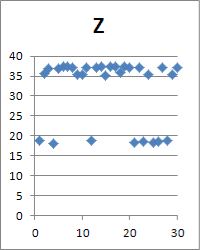
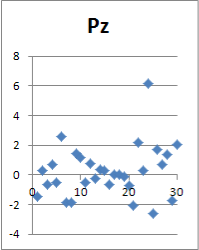
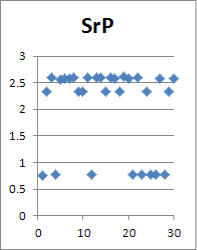
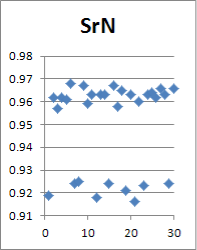
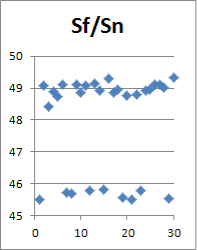
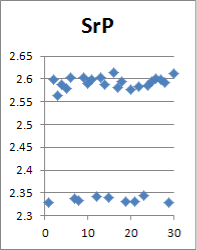
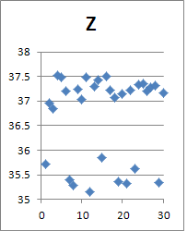
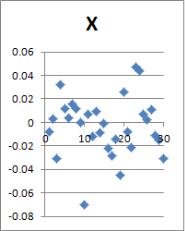
Учет случайной шероховатости исходной поверхности вала непременно вызовет случайное отклонение в параметрах сформированного соединения. В статье проводится анализ статистического ряда и определение его параметров, таких как математическое ожидание и среднеквадратическое отклонение. Для признания результатов статистической обработки корректными необходимо не менее N=30 реализаций (рис. 2).
|
|
|
|
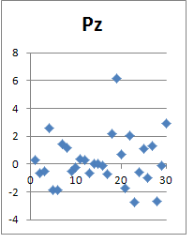
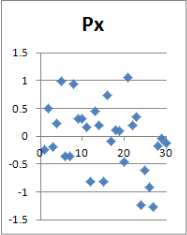
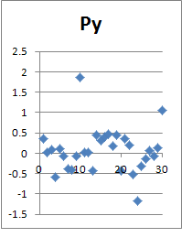
Рис. 2. Точечное отображение некоторых параметров
Поверхностный взгляд на данные в графическом точечном виде предполагает наличие восьми бракованных реализаций, учет которых при обработке статистики приведет к ошибкам в математическом ожидании и среднеквадратическом отклонении параметров реализаций. Их исключение позволит повысить в дальнейшем точность конечного результата, но потребуется дополнить статистический ряд минимум до 30-ти «хороших» реализаций (рис. 3, 4).
Перекрестный поверхностный анализ графиков (рис.3,4) позволяет целиком отбросить из статистического ряда еще раз девять реализаций по условию выхода за пределы точности (Z) и прочности (SrN, Sf/Sn, SrP), а оставшиеся реализации проверить по критерию наличия грубых ошибок с доверительной вероятностью 0,95 при 5 % уровне значимости по каждой колонке отдельно (табл.2).
|
|
|
|
Рис. 3. Параметры прочности соединения — обновленный ряд
|
|
|
|
|
|
|
|
Рис. 4. Параметры точности соединения — обновленный ряд
Таблица 2
Дополненный список реализаций сборки соединения
|
N |
Z |
X |
Y |
Pz |
Px |
Py |
Sf/Sn |
SrZ |
SrN |
SrP |
MaxP |
|
1 |
36.97 |
0.00 |
0.03 |
-0.64 |
0.50 |
0.02 |
49.07 |
-0.07 |
0.96 |
2.60 |
10.49 |
|
2 |
36.85 |
-0.03 |
-0.01 |
-0.52 |
-0.19 |
0.09 |
48.41 |
-0.09 |
0.96 |
2.56 |
10.20 |
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
7 |
37.03 |
-0.07 |
-0.01 |
-0.24 |
0.32 |
1.86 |
48.87 |
-0.07 |
0.96 |
2.59 |
9.93 |
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
24 |
37.35 |
0.01 |
0.05 |
0.44 |
0.70 |
0.08 |
48.58 |
-0.06 |
0.96 |
2.57 |
10.56 |
|
25 |
37.72 |
-0.01 |
0.05 |
-2.68 |
0.88 |
0.11 |
49.61 |
-0.06 |
0.98 |
2.62 |
10.05 |
|
26 |
37.18 |
-0.02 |
0.00 |
1.17 |
0.00 |
-0.36 |
49.20 |
-0.07 |
0.97 |
2.61 |
9.94 |
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
33 |
37.17 |
-0.03 |
-0.02 |
-0.55 |
-0.18 |
0.66 |
49.18 |
-0.08 |
0.97 |
2.60 |
10.67 |
|
34 |
37.23 |
-0.02 |
0.01 |
0.32 |
0.26 |
0.75 |
49.05 |
-0.08 |
0.96 |
2.60 |
10.11 |
|
|
37.30 |
0.00 |
0.00 |
0.19 |
0.02 |
0.05 |
49.00 |
-0.07 |
0.96 |
2.59 |
10.24 |
|
σ |
0.20 |
0.02 |
0.02 |
1.53 |
0.57 |
0.57 |
0.22 |
0.01 |
0.00 |
0.01 |
0.39 |
|
Xmax |
37.72 |
0.04 |
0.05 |
3.70 |
1.08 |
1.86 |
49.61 |
-0.05 |
0.98 |
2.62 |
11.04 |
|
Xmin |
36.85 |
-0.07 |
-0.06 |
-2.70 |
-1.27 |
-1.17 |
48.41 |
-0.09 |
0.96 |
2.56 |
9.75 |
|
n |
34 |
34 |
34 |
34 |
34 |
34 |
34 |
34 |
34 |
34 |
34 |
|
β1 |
2.14 |
2.02 |
2.02 |
2.33 |
1.89 |
3.21 |
2.85 |
2.14 |
3.45 |
2.41 |
2.13 |
|
β2 |
0.58 |
0.69 |
0.61 |
0.50 |
0.54 |
0.66 |
0.79 |
0.47 |
0.63 |
0.71 |
0.32 |
Методика поиска и исключения грубых ошибок состоит в следующем:
- В каждой колонке рассчитать среднее значение и среднеквадратическое отклонение статистического ряда. В MSExcel для этого есть стандартные функции “=СРЗНАЧ(…)” и “=СТАНДОТКЛОН(..)” с указанием интервала ячеек значений ряда.
- В каждой колонке определить максимальное, минимальное значение в ряду и количество значений ряда. В MSExcel для этого есть стандартные функции “=МАКС(…)”, “=МИН(…)”, “=СЧЕТ(…)” также с указанием интервала ячеек значений ряда.
-
В каждой колонке по формулам
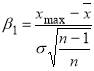и 
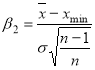определить весовую величину ошибки и сравнить ее с табличным значением критерия появления грубых ошибок (табл. 3). При n=34 величина 
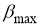=2.84.
-
Если выполняется условие
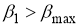или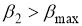 
, то значение 
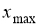или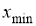 
необходимо исключить из ряда как грубую погрешность.
- После исключения грубых ошибок нужно повторить расчеты, начиная с пункта 1.
Таблица 3
Критерий появления грубых ошибок
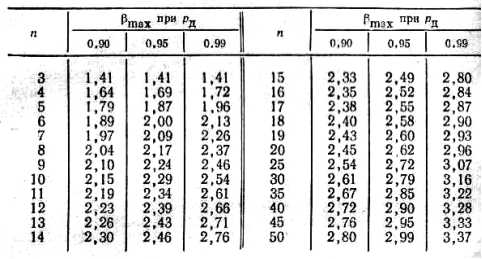
Обрабатывая таблицу 2 согласно методике, приведенной выше, найдено еще 3 грубых ошибки, 2 из которых указывают на бракованную реализацию № 25. При этом в реализации № 7 достаточно исключить само значение без исключения всей реализации. После исключения всех грубых ошибок к оставшимся в таблице реализациям допустимо применить методы обработки статистических данных для определения среднего значения и среднеквадратического отклонения параметров собранных соединений. Результаты обработки приведены в табл.4.
Таблица 4
Окончательная обработка статистических рядов
|
N |
Z |
X |
Y |
Pz |
Px |
Py |
Sf/Sn |
SrZ |
SrN |
SrP |
MaxP |
|
|
37.29 |
0.00 |
0.00 |
0.28 |
-0.01 |
-0.01 |
48.98 |
-0.07 |
0.96 |
2.59 |
10.24 |
|
σ |
0.19 |
0.02 |
0.02 |
1.46 |
0.56 |
0.49 |
0.19 |
0.01 |
0.00 |
0.01 |
0.39 |
|
Xmax |
37.65 |
0.04 |
0.05 |
3.70 |
1.08 |
1.06 |
49.32 |
-0.05 |
0.97 |
2.61 |
11.04 |
|
Xmin |
36.85 |
-0.07 |
-0.06 |
-2.70 |
-1.27 |
-1.17 |
48.41 |
-0.09 |
0.96 |
2.56 |
9.75 |
|
n |
33 |
33 |
33 |
33 |
33 |
32 |
33 |
33 |
33 |
33 |
33 |
|
β1 |
1.96 |
1.98 |
2.10 |
2.37 |
1.98 |
2.23 |
1.79 |
2.24 |
1.57 |
1.85 |
2.09 |
|
β2 |
0.58 |
0.68 |
0.65 |
0.55 |
0.56 |
0.63 |
0.70 |
0.48 |
0.50 |
0.66 |
0.32 |
Таким образом, из 55-ти суммарно выполненных реализаций, 22 расчетных реализации было отбраковано, а оставшихся 33 участвовали в наработке конечного результата.
Литература:
- Линейцев В. Ю. Контактная прочность, жесткость и точность разъёмных неподвижных конических соединений в инструментальных системах Диссертация на соискание ученой степени кандидата технических наук / Иркутск, 2006.
- Ильиных В. А., Линейцев В. Ю., Рожкова Е. А. Расчет напряженно-деформированного состояния ступицы с РК-профильным отверстиемСовременные технологии. Системный анализ. Моделирование. 2010. № 3. С. 69–73.
- Рожкова Е. А., Ильиных В. А., Линейцев В. Ю. Расчет на прочность РК-3-профильных соединений с натягомСовременные технологии. Системный анализ. Моделирование. 2012. № 2. С. 17–20.
- Линейцев В. Ю., Ильиных В. А. Имитационное моделирование деталей конического соединения на основе рk-3 профильных кривыхСовременные технологии. Системный анализ. Моделирование. 2015. № 2 (46). С. 51–55.
