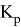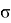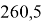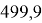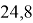Генетический алгоритм для автоматической настройки ПИД-регулятора



В статье рассматривается способ автоматической настройки ПИД-регулятора, поддерживающий изменение объекта управления, и его моделирование с помощью встроенных приложений вMATLAB.

Ключевые слова: генетический алгоритм, настройка ПИД-регулятора.

The article changes the usual PID controller settings that support changing the control object, and its implementation with built-in apps in MATLAB.

Keywords : genetic algorithm, PID controller tuning.

Пропорционально-интегрально-дифференциальные (ПИД) регуляторы десятилетиями широко используются в системах автоматического управления для задания выходного сигнала, с целью получения необходимых параметров для системы. Но они по-прежнему остаются плохо настроенными с использованием обычных методов настройки. Традиционный метод, например, такой как метод Цейглера — Никольса [1],который очень долго будет находить подходящие значения параметров ПИД-регулятора, а также невозможность его использования при настройке динамических объектов, параметры которых постоянно меняются. В таких системах мы должны выполнять перенастройку в режиме реального времени, что не может быть применено методами настройки, потому что мы должны сначала отключить систему, чтобы установить ее параметры.

В настоящее время главным направлением развития ПИД-регуляторов является разработка способа автоматической настройки, который позволит снизить затраты человеческого труда, избавляя от необходимости долгого процесса подбора коэффициентов регулятора. Такие методы автоматической настройки, были разработаны в 60-х годах [2], но активно стали использоваться только после появления микроконтроллеров.

В данной статье будет рассмотрен генетический алгоритм автоматической настройки, который получил широкое распространение к настоящему времени. Цель работы этого алгоритма заключается в нахождении лучшего варианта настройки по сравнению с имеющимся, а не оптимального решения задачи. Главными достоинствами этого алгоритма является отсутствие проблем со сходимостью и устойчивостью, а также, что сложность алгоритма мало зависит от сложности задачи. Из недостатков можно выделить большое время поиска экстремума, что не допускает их использование в быстродействующих системах.

Генетические алгоритмы основаны на принципах естественного отбора, сформулированных Дарвином в 1859 году. Основной идеей является прямое подобие принципу естественного отбора, когда выживают наиболее приспособленные особи.

Классическая схема генетического алгоритма состоит из следующих шагов — [3]:

1. выбор исходной популяции хромосом размера N;
2. оценка приспособленности хромосом в популяции;
3. проверка условия остановки алгоритма;
4. селекция хромосом;
5. применение генетических операторов;
6. формирование новой популяции;
7. переход к пункту 2.

Для использования этого алгоритма при настройке ПИД-регулятора изначально генерируется случайным образом исходная популяция (выборка), представляющая собой набор строк в двоичном коде, где каждая строка — это набор коэффициентов ПИД-регулятора (Kp, Ki, Kd). Такие образом проходя один цикл алгоритма лучшие варианты собираются в группу, где происходят скрещивания или мутации.Скрещивание позволяет получить от двух родителей перспективного потомка. Оператор мутации вносит изменения в хромосомы.

Оператор скрещивания. На первом этапе скрещивания выбираются пары хромосом из родительской популяции, выбранные в результате селекции (выбора лучших вариантов).Затем эти хромосомы объединяются в пары случайным образом.Здесь главным требованием для скрещивания является возможность потомков унаследовать черты обоих родителей, скрещивая их каким-либо способом.

Оператор мутации нужен для изменения случайно выбранного гена в хромосоме с какой-то определённом вероятностью. Вероятность мутации обычно выбирается очень малой. Т. к. именно мутации способны улучшить или ухудшить приспособленность хромосомы.

Пример кодирования трех коэффициентов ПИД-регулятора для применения в генетических алгоритмах приведен на рис.1 [4] После выполнения генетического алгоритма переводят двоичные значение в нормальный вид.

Рис. 1. Пример кодирования коэффициентов

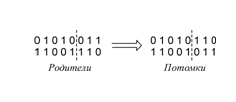
Рис. 2. Пример операции скрещивания

Оценка приспособленности хромосом в популяции для выбора коэффициентов ПИД-регулятора может быть выбрана как минимальное перерегулирования, минимальное время переходного процесса и т. д.

Моделирование генетического алгоритма в программной среде MATLAB

Для моделирования генетического алгоритма для настройки в MATLABиспользуется встроенное приложение OptimizationTool.В качестве объекта управления будем использовать передаточную функцию: .

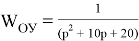
Optimization Tool представляет собой приложение для поиска параметров, которые минимизируют или максимизируют решения, удовлетворяя ограничениям. В нашем случае задачей оптимизации будет функция (gen_test), для которой будет выполняться генетический алгоритм. На вход функции будем подавать выборку из значений коэффициентов ПИД-регулятора (1), на выходе будем получать графики входного и выходного сигналов и ошибку J (в нашем случае является оценкой приспособленности). При использовании OptimizationTool размер популяции и количество поколений выбирается автоматически, а методы скрещивания и мутации используют следующие алгоритмы: скрещивание проводится в каждом поколении, а мутации только тогда, когда ошибка Jполучается равной прошлому набору коэффициентов.

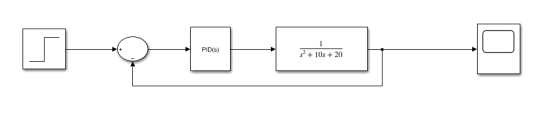
Рис. 3. Структурная схема настраиваемой системы

function [J] = gen_test(x)

s = tf('s');

plant = 1 / (s^2 + 10*s + 20); % передаточная функция объекта управления

Kp = x(1); % пропорциональный коэффициент

Ki = x(2); % интегральный коэффициент

Kd = x(3); % дифференцирующий коэффициент

cont = Kp + Ki/s + Kd * s; % передаточная функция пид-регулятора

step(feedback(plant*cont,1));% сигналступенькипослепид-регулятора и объекта управления

dt = 0.01;

t = 0:dt:1;

e = 1 - step(feedback(plant*cont,1),t); % разница входного и выходного сигналов

J = sum(t'.*abs(e)*dt)

end

В меню приложения выбираются алгоритм, который будет оптимизировать заданную функцию и параметры, по которым будет выполнена оптимизация. Настройки для моделирования генетического алгоритма для ПИД-регулятора представлена на рис.4.

В окне Solver выбирается тип алгоритма, по которому будет выполнена оптимизация, а в окне FitnessFunction– функция, которую нужно оптимизировать.

В окне Bounds указываются ограничения для переменных — верхняя и нижняя границы, в которых алгоритм будет выбирать набор коэффициентов.

Рис. 4. Меню встроенного приложения OptimizationTool

Для задачи настройки ПИД-регулятора количество переменных равно трём, где переменные — это коэффициенты регулятора (Kp, Ki, Kd). И вводится ограничение для этих коэффициентов в параметре Bounds, Lower– [0, 0, 0] и Upper– [500, 500, 500].

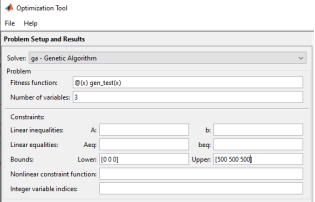
Рис. 5. Настройка приложения OptimizationTool

Далее запускается алгоритм оптимизации:

Алгоритм, пройдя 77 итерации, получил коэффициенты ПИД-регулятора:

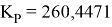
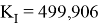
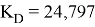
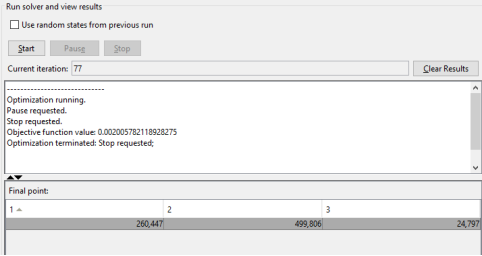
Рис. 6. Окно с полученными коэффициентами

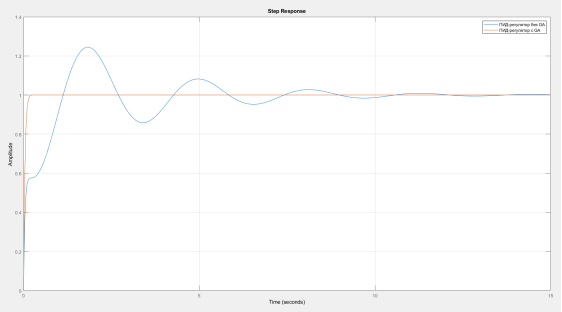
Рис. 7. Полученные переходные процессы для разных случаев настройки

Для нашего входного воздействия можно сравнить полученный выходной сигнал с сигналом, полученным с помощью автоматической настройкой в MATLABс помощью PIDTuner, который также позволяет получить входные сигнала с требуемыми параметрами.

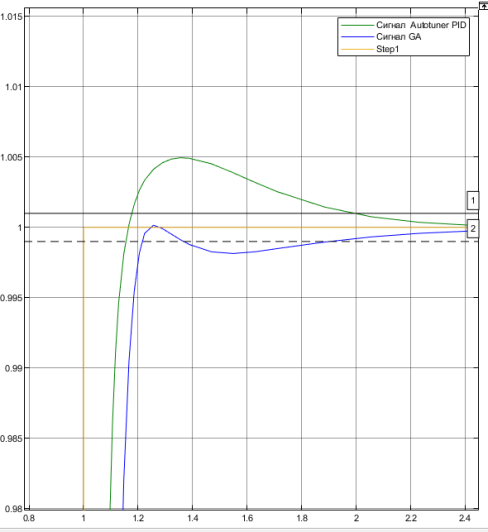
Рис. 8. Графики выходных сигналов при разных методах настройки.

Таблица 1

Полученные результаты для разных методов настройки

Метод настройки ПИД-регулятора				Перерегулирование , %	Время переходного процесса 𝜏 𝑐 , ,сек
PID AutoTuner MATLAB	400.96	934.2	41.7	0,5	2
Генетический алгоритм				0,2	1.9

Полученные результаты показывают, что при настройке ПИД-регулятора с помощью генетического алгоритма, выходной сигнал имеет меньшее по сравнению с автоматической настройкой значение перерегулирования и время переходного процесса.

Генетический алгоритм, примененный в ПИД-регуляторе, улучшает переходную характеристику по сравнению с автоматическим методом настойки, об этом свидетельствуют качественные характеристики выходного сигнала. Но подбор таких коэффициентов производится намного дольше.

Таким образом, по результатам, полученным после выполнения генетического алгоритма, можно сделать вывод о работоспособности промоделированного генетического алгоритма для нахождения оптимума для задачи с настройкой ПИД-регулятора. И позволяет использовать этот алгоритм как прототип для дальнейшей модернизации, например, для решения проблем с качеством настройки, влиянием нелинейности объекта и т. д., однако, нужно будет учитывать проблему сходимости, при использовании генетического алгоритма.

Литература:

1. Бункин П. Я. Типовые регуляторы систем управления. Дальневосточный федеральный университет, 2013
2. Справочник по теории автоматического управления. Под ред. А. А. Красовского. — М.: Наука, 712 с (2009)
3. Гладков Л. А., Курейчик В. В., Курейчик В. М. Генетические алгоритмы. — Москва, Физматлит, 2006, 320 с.
4. Li J., Xie J.-Y.; Wu Z.-M. Design of Disturbance Rejection PID Controllers for Time Delay System Based on Genetic Algorithms. -Neural Networks and Brain, 2005. ICNN&B '05. International Conference on. vol. 2, 13–15 Oct. 2005, p.876–880.