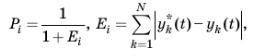В статье рассматривается принцип использования генетического алгоритма для оптимизации управления температурным режимом печи коксования. Приведен анализ качества переходных процессов с традиционным ПИД-регулятором и нейросетевым супервизором.
Ключевые слова: нейронная сеть, нейросетевое управление, ПИД-регулятор, нейронный супервизор, объект управления.
Печи установок коксования работают в жестких условиях, которые характеризуются значительной температурой нагрева сырья и малыми допустимыми отклонениями ее от заданного значения. Даже непродолжительное отклонение температуры от заданной приводит к закоксовыванию и прогару труб, нарушению норм технологического регламента, а также сокращению времени межремонтного пробега [1].
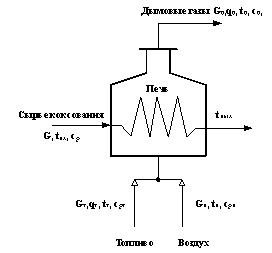
Рассмотрим особенности печи коксования, с точки зрения регулирования процесса горения. Задача регулирования состоит в поддержании заданного значения выходной температуры потока: tвых = t0вых (см. рис.1).
|
|
|
|
Рис. 1. Принципиальная схема печи |
Рис. 2. Структурная схема |
Тепловой баланс для сырья коксования имеет вид [9]:
![]() (1.1)
(1.1)
Из уравнения 1.1 определим температуру в зоне горения tг для процесса горения:
![]() (1.2)
(1.2)
Отсюда: ![]() (1.3)
(1.3)
где Gт, Gв, Gд, G — расходы топлива, воздуха, дымовых газов и сырья коксования;
срт, срв, срд, ср- удельные теплоемкости веществ;
tт, tв, tвх — входные температуры топлива, воздуха, сырья коксования;
tд, tвых — выходные температуры дымовых газов и нагреваемого потока сырья коксования;
![]() - коэффициент соотношения расходов воздуха и топлива.
- коэффициент соотношения расходов воздуха и топлива.
Из уравнения теплового баланса (1.1) с учетом (1.3) находим формулу для определения выходной температуры:
![]() (1.4)
(1.4)
Если tт = tв, то
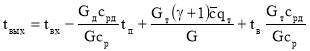 (1.5)
(1.5)
где ![]() (1.6)
(1.6)
Анализируя трубчатую печь коксования как объект регулирования, получим структурную схему, показанную на рис. 2. Возмущающими воздействиями приняты расход и температура сырья коксования на входе, коэффициент теплопередачи и теплопотери; основными регулирующими воздействиями — расходы топлива и воздуха. К выходным параметрам отнесена выходная температуры сырья коксования и дымовых газов. Помимо требований к режимным параметрам радиационной печи коксования накладываются ограничения из условий взрывобезопасности и требований охраны труда и защиты окружающей среды [2]. В частности, коэффициент соотношения расходов воздуха и топлива γ должен удовлетворять ограничению γн γ γв. Для предотвращения попадания дымовых газов в атмосферу в трубчатых печах поддерживается разрежение.
Рассмотрим пример автоматизации печи, обеспечивающая поставленную задачу регулирования (рис. 3).
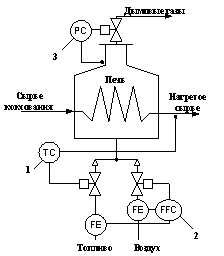
Рис. 3. Пример автоматизации печи коксования
Данный вариант представляет систему автоматизации, состоящую из трех контуров регулирования. Регулятор 1 стабилизирует выходную температуру сырья коксования на заданном значении. Второй регулятор обеспечивает соотношение расходов воздуха и топлива, поступающих в зону горения печи. Третий регулятор поддерживает разряжение в печи путем отвода дымовых газов. Предложенный пример будет удовлетворять всем требованиям управления только в случае стационарности параметров процесса. Однако если параметры процесса будут изменяться по неизвестным законам или носить хаотичный характер, то обеспечить автоматическую подстройку регуляторов не представляется возможным. Для решения данной проблемы необходима адаптация регуляторов на основе искусственных нейронных сетей. В данном случае применим нейронное супервизорное управление на основе генетического алгоритма.
Генетический алгоритм использует базовые представления об эволюции как о циклическом процессе смены популяций, в котором наибольшее потомство дают наиболее приспособленные особи, а новые свойства индивидуумов возникают при мутациях. Популяция состоит из хромосом, кодирующих решение некоторой задачи оптимизации [3]. Общая схема ПИД-регулятора с нейронным супервизором приведена на рис. 4.

Рис. 4. Структурная схема ПИД-регулятора с нейронным супервизором
В рассматриваемом объекте управления выделим линейную динамическую часть и нелинейную статическуя часть (рис. 5).
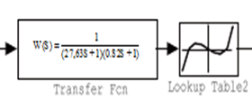
Рис. 5. Нелинейный объект управления в MatLab Simulink
Настройка ПИД-регулятора для линейной части (колебательное звено) средствами оптимизации MatLab не представляет трудностей. Однако при введении нелинейности качество оптимизации коэффициентов заметно ухудшается. Таким образом, при постоянных значениях коэффициентов ПИД-регулятора не удается добиться хорошего качества управления. Для оперативного изменения коэффициентов будем также использовать двухслойную ИНС прямого распространения, содержащую по три нейрона в каждом слое (рис. 6). На рис. 6 цифрами обозначены отдельные нейроны. Нейроны 1-го слоя имеют активационную функцию — гиперболический тангенс, а у нейронов 2-го слоя активационные функции линейные. На вход НС поступают текущее и задержанное значения ошибки. Число линий задержки соответствует порядку динамической части объекта управления. Величина задержки зависит от скорости протекания переходного процесса, она может быть выбрана в пределах 0,01–0,1 с.
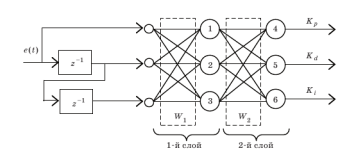
Рис. 6. Структура нейросетевого супервизора
Задача конструирования нейросетевого супервизора подразумевает, таким образом, настройку двух весовых матриц W1 и W2, содержащих по девять весов каждая. Использование для настройки алгоритма обратного распространения ошибки в данной ситуации оказывается затруднительным, поскольку невозможно сформировать обучающую выборку для НС. Использование ГА предполагает кодирование параметров супервизора, т. е. весов НС, хромосомой длиной 18 действительных чисел (генов).
Хромосома представляет собой альтернативное решение задачи. Совокупность всех хромосом образует популяцию. Популяция эволюционирует под воздействием генетических операторов отбора, скрещивания и мутации. Для выполнения операции отбора необходимо иметь описание пригодности каждой хромосомы Pi. Эта оценка может быть найдена путем сравнения эталонного описания переходного процесса y*(t) и переходного процесса, полученного под управлением i-й хромосомы. Например:
|
|
где N — рассматриваемое число точек переходного процесса.
На рис. 7 приведена схема моделирования работы нейросетевого супервизора в MatLab Simulink.
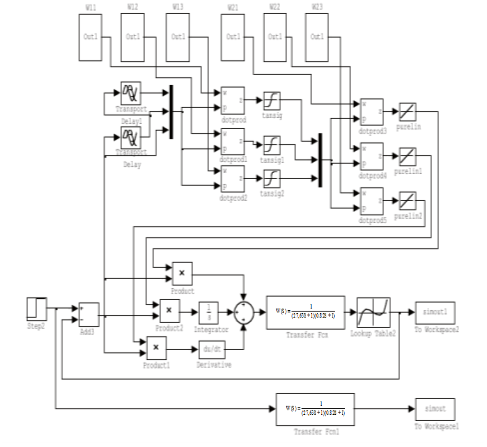
Рис. 7. Схема моделирования работы нейросетевого супервизора в MatLab Simulink
В нижней части рис. 7 представлена передаточная функция, служащая для описания эталонного процесса. Блоки simout и simout 1 служат для накопления точек эталонного и реального переходного процесса. Обучение супервизора выполнялось с помощью стандартного инструмента gatool в составе MatLab. Размер популяции 50 хромосом, для поиска решения потребовалось около 100 генераций. Были получены следующие весовые матрицы:
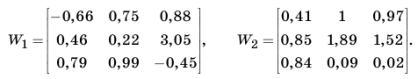
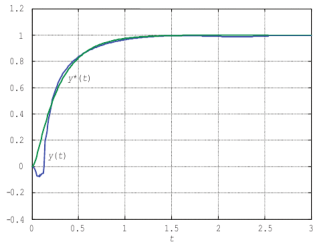
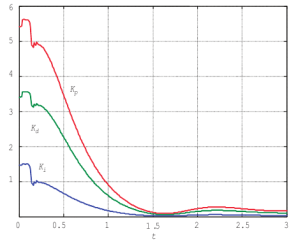
На рис. 8 приведен переходный процесс в системе после обучения нейронного супервизора. На рис. 9 показаны графики изменения значений коэффициентов ПИД-регулятора во время переходного процесса.
|
Рис. 8. Переходные процессы в системе с нейронным супервизором |
Рис. 9. Изменение коэффициентов ПИД-регулятора во время переходного процесса |
Как следует из рис. 9, переходный процесс оказывается весьма близок к эталонному процессу, и ПИД-регулятор с супервизором обеспечивает гораздо более высокое качество управления, чем ПИД-регулятор с постоянными коэффициентами.
Литература:
- Селевцов Л. И. Автоматизация технологических процессов. 3-е изд. — М.: Академия, 2014. — 352 с.
- Ившин В. П. Современная автоматика в системах управления технологическими процессами. Учебное пособие. — М.: Инфра-М, РИОР. — 2015. — 272 с.
- Бураков М. В. Нейронные сети и нейроконтроллеры: учеб. пособие/ М. В. Бураков. — СПб.: ГУАП, 2013. — 284 с.: ил.