Надёжная эксплуатация агрегатов роторного типа в значительной степени определяется качеством их вибрационной отстройки от резонансов. Надежность методов расчета критических частот в значительной степени зависит от достоверности данных о податливостях опор, и что очень важно, от способа схематизации расчетной схемы динамической системы и учёта свойств элементов системы, участвующих в колебательном процессе.
Влияние упруго-массовых свойств опор на динамические характеристики системы «ротор – подшипники – опоры» рассматривалось в работах [1-5].
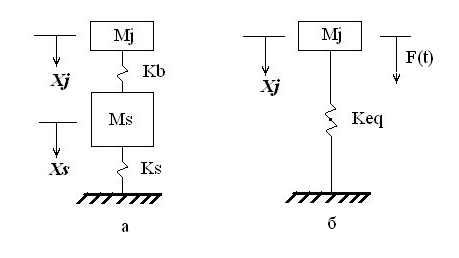
В работе [3] показано, что система с двумя степенями
свободы (рис.1а), может быть сведена в ряде случаев к эквивалентной
системе c одной степенью свободы (рис.1б),
при условии, что эквивалентная жесткость в этой системе определится
из условия: 
(1)
Рис. 1. Система с двумя степенями свободы (а)
и
эквивалентная ей система с одной степенью свободы (б) [3]
Если представить, что эквивалентная
система есть масса, опирающаяся на опору с указанными свойствами, то
из (1) следует, что эквивалентная жесткость опоры является функцией
не только жесткостей упругих элементов, но и массы опоры
и частоты вынужденных колебаний
.
Выражение
является, по сути, динамической жесткостью опор, изменяющейся от
значения статической жесткости
(при до
значения равного нулю при резонансе опоры (
)
и принимающей отрицательное значение при частоте выше резонансной
(
),
что подчеркивает смещение опоры в зарезонансной зоне в направлении
противоположном направлению действия силы.
Анализируя формулу (1) видно, что при массе опоры равной нулю (или пренебрежительно малой) формула (1) сводится к известному соотношению для жесткости двух последовательно соединенных упругих элементов:
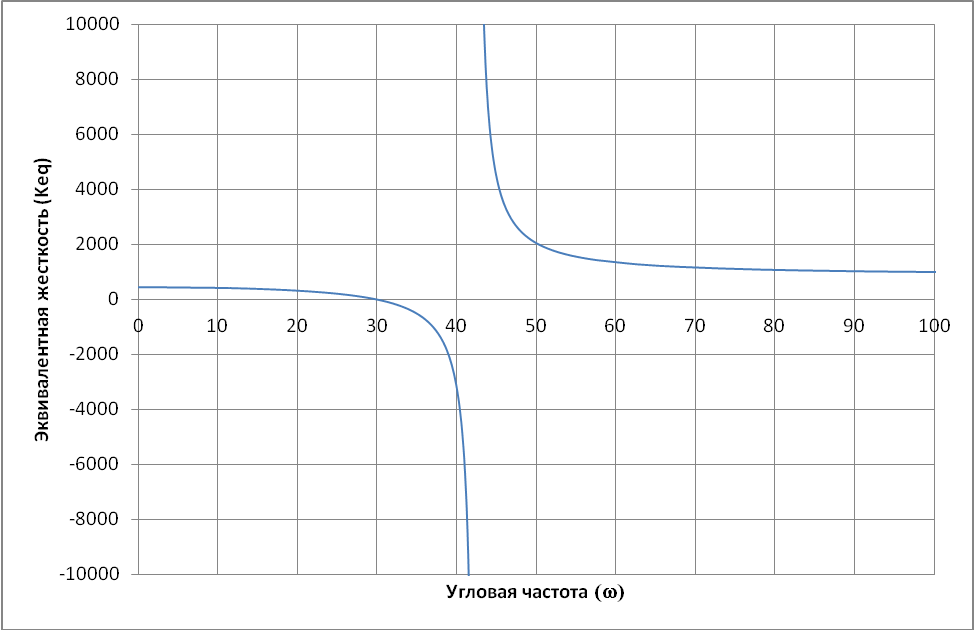
Характер зависимости эквивалентной жесткости от частоты колебаний показан на рис.2 для модели с параметрами Кb = Ks = 900, M = 1.
Рис. 2. Зависимость эквивалентной жесткости от частоты возбуждения
Из формулы (1) и рис.2 видно, что,
почти сразу за резонансом опоры, ее эквивалентная жесткость резко
возрастает, достигая значений
,
а затем стремится к значению жесткости
.
Рассмотрим теперь влияние параметров упруго-массовых опор на критические частоты системы «ротор – подшипники – опоры». Опоры представим как элементы с сосредоточенной массой Моп и жесткостью Коп. Ротор же представляется как система с распределенными параметрами, т.е. системой со многими степенями свободы.
Расчетная схема рассматриваемой модели представляет собой вал постоянного сечения диаметром d=250 мм и длиной L=5000 мм, разбитый на N=25 участков, опирающийся на два одинаковых подшипника, установленных в двух одинаковых опорах. Общая масса ротора mрот=1200 кг. Жесткость масляного слоя подшипника (аналог жесткости Kb) принята Км.с.=100000 Н/мм, конструктивная жесткость опоры (аналог Ks) принята Коп=100000 Н/мм. Масса каждой из опор Моп = 1500 кг.
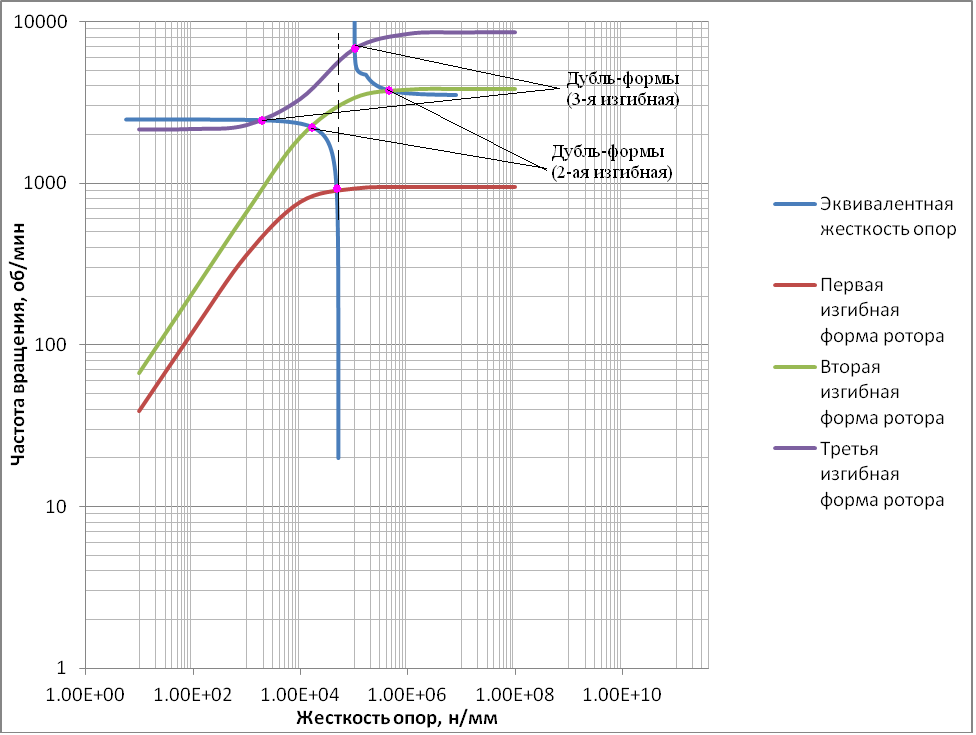
На рис.3 представлена так называемая карта критических частот исследуемого ротора, вычисленная в пакете программ DyRoBeS Rotor. Карта представляет собой зависимость критических частот ротора от жесткости опор, т.е. карта не учитывает каких – либо параметров конкретных опор.
С целью объяснения механизма качественной зависимости критических частот от приведенной жесткости опор на тот же график (рис. 3) нанесены линии эквивалентной жесткости опор, вычисленной по формуле (1). Собственная частота опор в рассматриваемом случае составила 2467 мин-1
Точки пересечения эквивалентной жесткости опор с линиями собственных частот соответствующих форм колебаний ротора и являются критическими частотами ротора на указанных опорах. На рис.3 эти точки выделены и отмечены выносками.
Рис. 3. Зависимость критических частот от эквивалентной жесткости опор
Но тогда выясняется, что в системе «ротор – подшипники – опоры», при определенных упруго-массовых свойствах опор, одни и те же изгибные формы колебаний ротора могут реализоваться неоднократно!
Рис. 4. Формы колебаний ротора: а) 1-ая - 904 об/мин,
б) 2-я – 2239 об/мин, в) 3-я – 2439 об/мин, г) 4-я - 3726 об/мин, д) 5-я – 6979 об/мин.
На рис. 4 показаны формы колебаний ротора и приведены соответствующие им значения собственных частот. Из рис. 4 видно, что действительно после первой и второй собственных частот, имеющих значения 904 и 2239 об/мин и соответствующих первой и второй изгибным формам ротора, реализуется третья изгибная форма на очень податливых опорах (2439 об/мин), частота которой несущественно отличается от частоты резонанса опор (2467 об/мин). Далее снова последовательно реализуются вторая и третья изгибные формы колебаний ротора, но уже на опорах со значительно большей жесткостью. Таким образом, рассматриваемая система «ротор – подшипники – опоры» характеризуется наличием «дубль-форм», которые реализуются с деформациями близкими по форме. Причем, каждая из «дубль-форм», являясь достаточно ортогональной к другим собственным формам ротора, не оказываются ортогональными к друг другу. Следствием этого является, что устраняя при балансировке неуравновешенность по одной из «дубль-форм» (уменьшая упругие деформации), в значительной степени устраняется неуравновешенность и по другой.
Выявленный в результате аналитического и численного анализа эффект повторяемости изгибных форм колебаний ротора («дубль-эффект») объясняет механизм появления целого ряда дополнительных резонансов или критических частот, наблюдаемых при экспериментальных исследованиях агрегатов роторного типа и не соответствующих расчетам, выполненным только с учетом жесткостей маслянного слоя в подшипниках и опор.
Литература:
Вибрации в технике: Справочник. В 6-ти т. / Ред. совет: В.Н. Челомей (пред.). – М.: Машиностроение, 1980, - Т. 3. Колебания машин, конструкций и их элементов / Под. ред. Ф.М. Диментберга и К.С. Колесникова, 1980.
Биргер И.А., Шорр Б.Ф, Иосилевич Г.Б. Расчеты на прочность деталей машин: справочник. М., 1993.
Introduction to Dynamics of Rotor-Bearing Systems / Wen Jeng Chen, Edgar J. Gunter.
Пановко Я.Г. Введение в теорию механических колебаний. — М.: Наука 1991 г.
Тимошенко С.П. Колебания в инженерном деле. М.: «Наука», 1967.