В работе рассматривается некоторый квадрат и куб в поле р-адических чисел.
Ключевые слова : поле рациональных чисел, р-адическая норма, поле р-адических чисел.
1. Введение. Внастоящее время различные структуры изучаются над полем p-адических чисел. Теория p -адических чисел является одним из самых популярных и бурно развивающихся направлений современной математики. На данный момент известны p -адическая математическая физика, p -адическая теория вероятностей, p -адические дифференциальные уравнения, p -адические динамические системы и др. p -адические числа впервые были введены в конце XIX века в работе немецкого математика К. Гензеля.
Поле р-адических чисел не является алгебраическим замкнутым. Поэтому в работе Владимиров В.С, Волович И. Б. и Зеленов Е. И. дано критерия разрешимости р -адического квадратного уравнения [1, c-28].
Напомним определение поля р -адических чисел.
Пусть
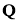
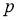
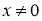
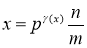
где
m
,
n
,
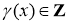
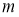
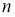
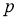
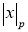
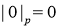
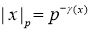
Норма
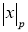
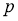
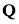
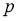
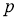
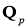
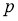
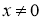
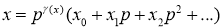
где
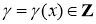
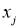
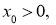
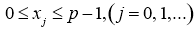
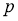
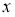
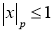
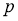
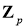
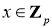
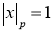
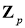
В работе [1] дано критерия разрешимости квадратных уравнений.
Теорема 1 [1]. Для того чтобы уравнение
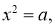
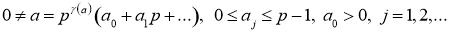
имело решение
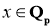
1)
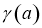
2)
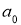
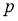
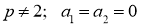
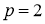
Напомним, что число
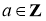
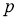
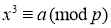
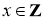
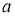
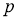
В работе [2] приведено критерия разрешимости уравнения
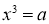
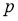
Теорема 2 [2].
Пусть
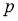
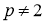
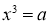
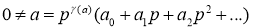
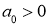
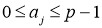
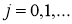
имело решение х
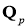
3)(a) — кратное на 3,
4)а0 является кубическим вычетом по модулю р, если
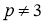
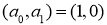
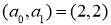
Замечание 1 [2].
Условие 2 теоремы 1 при p=2 всегда выполняется, следовательно, уравнение
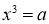
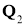
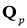
Основными результатами являются следующие утверждения.
Предложение 1.
Выражение
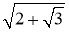
Доказательство
. Первый шаг докажем, что
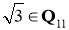
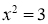
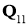
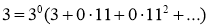
Первое условия теоремы 1 выполняется. Вторая условия теоремы 1 также выполняется, так как сравнение
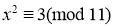
имеют решение
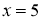
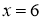
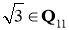
Второй шаг нам надо разрешимо ли
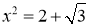
в поле 11-адических чисел. Сначала разложим число
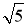
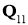
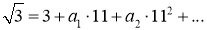
где
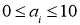
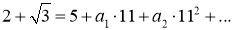
Первое условия теоремы 1 выполняется, а выполнение второй условий теоремы 1 проверяется разрешимости сравнение
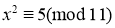
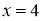
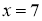
Предложение 2.
Выражение
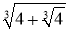
Доказательство . Используя условия теоремы 2, доказывается аналогичным образом как предложение 1.
Литература:
- Vladimirov V. S., Volovic I. B., Zelenov E.I, p-adic Analysis and Mathematical Physics. // World Scientific. Singapore. — 1994. — P. 352.
- Масутова К. К., Классификация шестимерных филиформных p -адических алгебр Лейбница. УзМЖ, 2011, № 4, С 115–124.







