Рассматривается задача Коши для алгебро-дифференциального уравнения первого порядка, возмущенного операторной добавкой в правой части, содержащей малый параметр. Перед производной находится вырожденный операторный коэффициент. Этот коэффициент является фредгольмовским оператором с нулевым индексом, имеющим одномерное ядро. В работе приводится алгоритм исследования задачи на наличие явления погранслоя, вызываемым наличием малого параметра. Алгоритм иллюстрируется примером с конкретными значениями операторных коэффициентов.
Ключевые слова: задача Коши, алгебро-дифференциальное уравнение, фредгольмов оператор, малый параметр, явление погранслоя, уравнение ветвления.
Рассматривается задача Коши:
![]() (1)
(1)
![]() (2)
(2)
где ![]() ,
, ![]() ,
, ![]() — замкнутые линейные операторы, действующие из банахова пространства
— замкнутые линейные операторы, действующие из банахова пространства ![]() в банахово пространство
в банахово пространство ![]() с всюду плотной в
с всюду плотной в ![]() областью определения;
областью определения; ![]() — голоморфная в окрестности точки
— голоморфная в окрестности точки ![]() функция;
функция; ![]() ;
; ![]() .
.
Уравнением (1) описывается межотраслевой баланс [1], продольные колебания молекул ДНК, подача сырья при работе лесопромышленной системы [2] и т. д.
Исследуется влияние малого параметра ![]() на качественные свойства решения. В случае вырожденного оператора
на качественные свойства решения. В случае вырожденного оператора ![]() это влияние может быть значительным, вплоть до разрушения системы. Иллюстрацией этого является «эффект бабочки» ‒ незначительное влияние на систему может иметь большие и непредсказуемые последствия в другом месте и в другое время.
это влияние может быть значительным, вплоть до разрушения системы. Иллюстрацией этого является «эффект бабочки» ‒ незначительное влияние на систему может иметь большие и непредсказуемые последствия в другом месте и в другое время.
В экономике (динамический межотраслевой баланс (Леонтьев)) невыполнение условий регулярности вырождения влечет большое расхождение между планируемым объемом производства (![]() ) и полученным на практике.
) и полученным на практике.
Пример исследования этой модели на наличие явления погранслоя приведен в [3].
Малый промежуток (в данном случае ![]() ), в котором происходит резкое изменение решения, называется пограничным слоем (погранслоем).
), в котором происходит резкое изменение решения, называется пограничным слоем (погранслоем).
К вырожденным относятся операторы, обладающие свойством фредгольмовости.
Приведем необходимые сведения.
Свойство. Линейный оператор ![]() , действующий из банахова пространства
, действующий из банахова пространства ![]() в банахово пространство
в банахово пространство ![]() , обладает свойством фредгольмовости (с нулевым индексом), если имеют место следующие разложения в прямые суммы подпространств
, обладает свойством фредгольмовости (с нулевым индексом), если имеют место следующие разложения в прямые суммы подпространств
![]() (3)
(3)
где ![]() — ядро оператора
— ядро оператора ![]() ,
, ![]() — прямое дополнение к ядру,
— прямое дополнение к ядру, ![]() — образ оператора
— образ оператора ![]() ,
, ![]() — дефектное подпространство; размерности
— дефектное подпространство; размерности ![]() ; сужение
; сужение ![]() оператора
оператора ![]() на
на ![]() имеет ограниченный обратный
имеет ограниченный обратный ![]() [4].
[4].
Замечание 1. Всякий линейный оператор ![]() , задаваемый вырожденной квадратной матрицей, фредгольмов [5].
, задаваемый вырожденной квадратной матрицей, фредгольмов [5].
Замечание 2. Всякий линейный оператор ![]() , задаваемый числовой матрицей, ограничен [6].
, задаваемый числовой матрицей, ограничен [6].
Определение 1. Ограниченная функция ![]() , определенная на
, определенная на ![]() , называется функцией погранслоя вблизи точки
, называется функцией погранслоя вблизи точки ![]() , если при
, если при ![]() имеет место следующее поведение:
имеет место следующее поведение: ![]() на
на ![]() для любых
для любых ![]() и
и ![]() на
на ![]() [7].
[7].
Определение 2. Взадаче (1), (2) имеет место явление погранслоя, если
где ![]() — решение предельной задачи для задачи (1), (2). Условия, при которых имеет место явление погранслоя, называются условиями регулярности вырождения.
— решение предельной задачи для задачи (1), (2). Условия, при которых имеет место явление погранслоя, называются условиями регулярности вырождения.
1. Исследование задачи (1), (2) на явление погранслоя
Перейдем к исследованию задачи (1), (2) на наличие явления погранслоя.
Здесь и далее рассматривается случай фредгольмова оператора ![]() , имеющего одномерное ядро.
, имеющего одномерное ядро.
Вводится: проектор ![]() на
на ![]() , полуобратный оператор
, полуобратный оператор
![]() :
: ![]() , где
, где ![]() обозначен единичный оператор в соответствующем подпространстве. Фиксируются элементы
обозначен единичный оператор в соответствующем подпространстве. Фиксируются элементы ![]() ,
, ![]() ,
, ![]() . В
. В ![]() вводится скалярное произведение
вводится скалярное произведение ![]() так, что
так, что ![]() .
.
Задача (1), (2) называется допредельной. А задача, в которой формально положено ![]() :
:
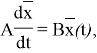
![]()
называется предельной. Предельная задача с данными из настоящего введения решена в работе [8].
Зададим условие.
-
Операторная пара (
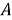 ,
, 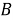 ) регулярна.
) регулярна.
Определение 3. Последовательность элементов ![]() ,
, ![]() , определяемых формулой
, определяемых формулой
![]()
назовем B-жордановой цепочкой ![]() .
.
Теорема 1. Операторная пара (![]() ,
, ![]() ) регулярна тогда и только тогда, когда -жорданова цепочка
) регулярна тогда и только тогда, когда -жорданова цепочка ![]() конечна [8].
конечна [8].
Приведем результаты, полученные в работах [9], [10].
Вводится сумма по всевозможным перестановкам из ![]() элементов
элементов ![]() и
и ![]() элементов
элементов ![]() :
:
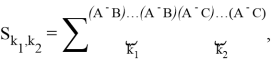
операторы, действующие из ![]() в
в ![]() :
:
![]()
![]()
![]()
![]()
коэффициенты ![]() , определяемые равенствами
, определяемые равенствами
![]()
Получено уравнение ветвления, помогающее выявлять наличие явления погранслоя в задаче и определять вид функций погранслоя
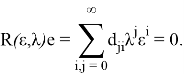
Регулярность операторной пары ![]() означает, что существует [8]
означает, что существует [8]
![]()
Число ![]() ‒ это длина B-жордановой цепочки
‒ это длина B-жордановой цепочки ![]() .
.
Замечание 3. При ![]() имеет место равномерная сходимость решения задачи (1), (2) крешению предельной задачи.
имеет место равномерная сходимость решения задачи (1), (2) крешению предельной задачи.
Предположим далее, что
Кроме того, зададим еще условия.
-
Операторы
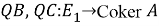 ,
, 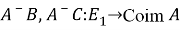 ограничены.
ограничены.
-
Существует такое число
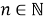 , что
, что
![]()
Тогда имеет место
Теорема 2. Пусть выполнены условия 1–3. В задаче (1), (2) имеет место явление погранслоя при выполнении условия
![]() (4)
(4)
2. Исследование одного линейного оператора на свойство фредгольмовости
Предложение. Линейный оператор ![]()
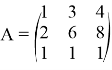
фредгольмов.
Доказательство. Строим подпространства:
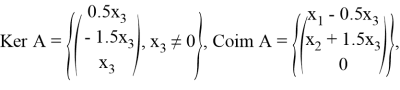
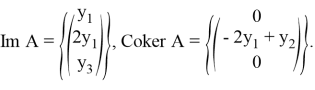
Ядро и коядро конечномерны и имеют единичную размерность. Выполнение ![]() ,
, ![]() влечет разложения (3). Оператор
влечет разложения (3). Оператор
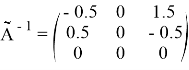
ограничен. Далее,
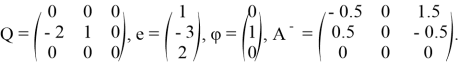
следовательно, ![]() фредгольмов.
фредгольмов.
3. Пример
Исследовать на наличие явления погранслоя следующую задачу Коши в ![]() , заданную на отрезке
, заданную на отрезке ![]() :
:
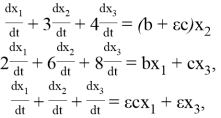 (5)
(5)
![]() (6)
(6)
где
1. Выпишем матрицы линейных операторов ![]() :
:
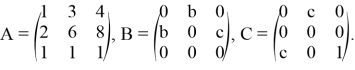
2. Оператор ![]() фредгольмов, что было доказано в предыдущем пункте.
фредгольмов, что было доказано в предыдущем пункте.
3. Проверим условие 1. Вычисления показывают, что
![]()
Следовательно, если ![]() , то
, то ![]() : операторная пара
: операторная пара ![]() регулярна, длина B-жордановой цепочки оператора
регулярна, длина B-жордановой цепочки оператора ![]() равна
равна ![]() .
.
Пусть теперь ![]() . Имеем:
. Имеем:
![]()
Поскольку ![]() (так как по условию
(так как по условию ![]() ), следовательно, операторная пара
), следовательно, операторная пара ![]() регулярна, длина B-жордановой цепочки оператора
регулярна, длина B-жордановой цепочки оператора ![]() равна
равна
![]() .
.
- Проверим условие 2. Операторы
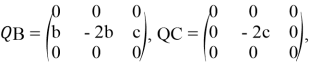
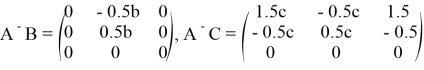
ограничены в силу замечания 2.
-
Проверим условие 3, вычислив значения
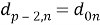 при каждом
при каждом 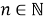 :
:
![]()
Оно выполнено, поскольку по условию ![]() .
.
- Далее,
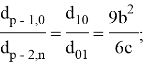
тогда неравенство (4) будет выполнено при условии ![]() .
.
Тем самым, применив замечание 3 и теорему 2, получим следующий результат.
Теорема 3. При выполнении условия ![]() имеет место равномерная сходимость решения допредельной задачи (5), (6) кпредельной задаче.
имеет место равномерная сходимость решения допредельной задачи (5), (6) кпредельной задаче.
Теперь пусть ![]() . При выполнении условия
. При выполнении условия ![]() в задаче (5), (6) имеет место явление погранслоя.
в задаче (5), (6) имеет место явление погранслоя.
Литература:
- Экономико-математические методы и модели. Под ред. А. В. Кузнецова, Минск, БГЭУ, 2000.
- Игнатенко, В. В. Моделирование и оптимизация процессов лесозаготовок / В. В. Игнатенко, И. В. Турлай, А. С. Федоренчик. — Учебное пособие для студентов по специальности «Лесоинженерное дело». — Мн.: БГТУ, 2004.
- Кащенко, М. А. Исследование возмущенной модели Леонтьева межотраслевого баланса / М. А. Кащенко, В. И. Усков // Материалы международной научной конференции «Воронежская зимняя математическая школа — 2020». — Воронеж: ИПЦ «Научная книга», 2020. — С. 147–149.
- Никольский, С. М. Линейные уравнения в линейных нормированных пространствах / С. М. Никольский // Изв. АН СССР. Серия математическая. — 1943. — Т. 7, вып. 3. — С. 147–166.
- Гельфанд, И. М. Лекции по линейной алгебре / И. М. Гельфанд. — Москва: Добросвет, МЦНМО, 1998. — 320 с.
- Бирман, М. Ш. Функциональный анализ / М. Ш. Бирман, Н.Я Виленкин,Е. А. Горин. — М.: Наука, 1972. — 544 с.
- Zubova, S. P. The role of perturbations in the Cauchy problem for equations with a Fredholm operator multiplying the derivative / S. P. Zubova // Doklady Mathematics. — 2014. — Vol. 89. — P. 72–75.
- Зубова, С. П. Сингулярное возмущение линейных дифференциальных уравнений, неразрешенных относительно производной / С. П. Зубова. — Автореф. дисс. … канд. физ.-мат. наук. — Воронеж, 1973. — 11 с.
- Zubova, S. P. Asymptotic Solution of the Cauchy Problem for a First-Order Equation with a Small Parameter in a Banach Space. The Regular Case / S. P. Zubova, V. I. Uskov // Mathematical Notes. — 2018. — Vol. 103, no. 3. — P. 395–404.
- Усков, В. И. О погранслое для дескрипторного уравнения с малым параметром / В. И. Усков // Актуальные направления научных исследований XXI века: теория и практика: сборник научных трудов по материалам международной заочной научно-практической конференции «Прикладная математика. Математическое моделирование систем и механизмов». — Воронеж: ВГЛТУ, 2017. — № 10, ч. 5 (36). — С. 541–543.







