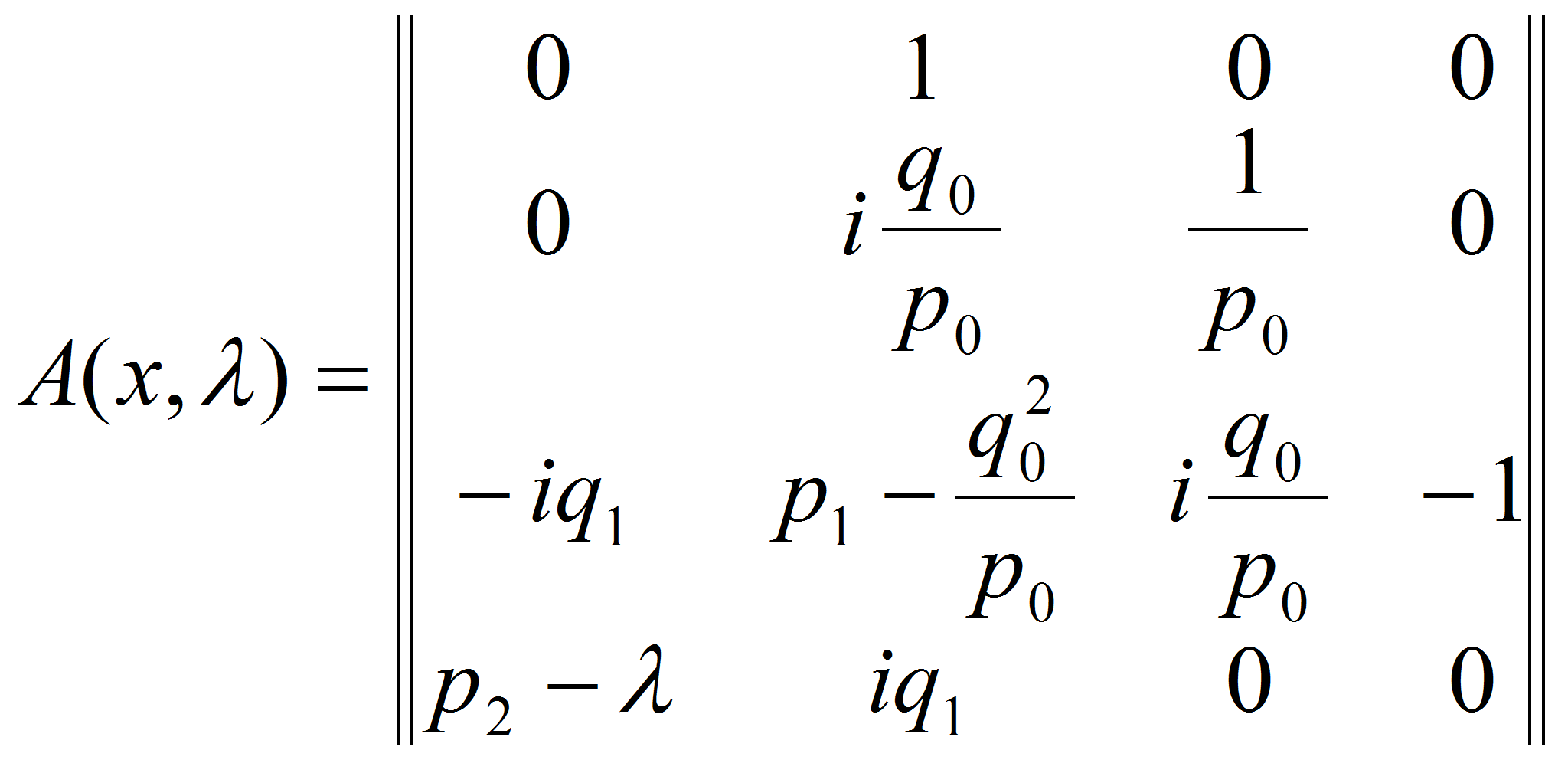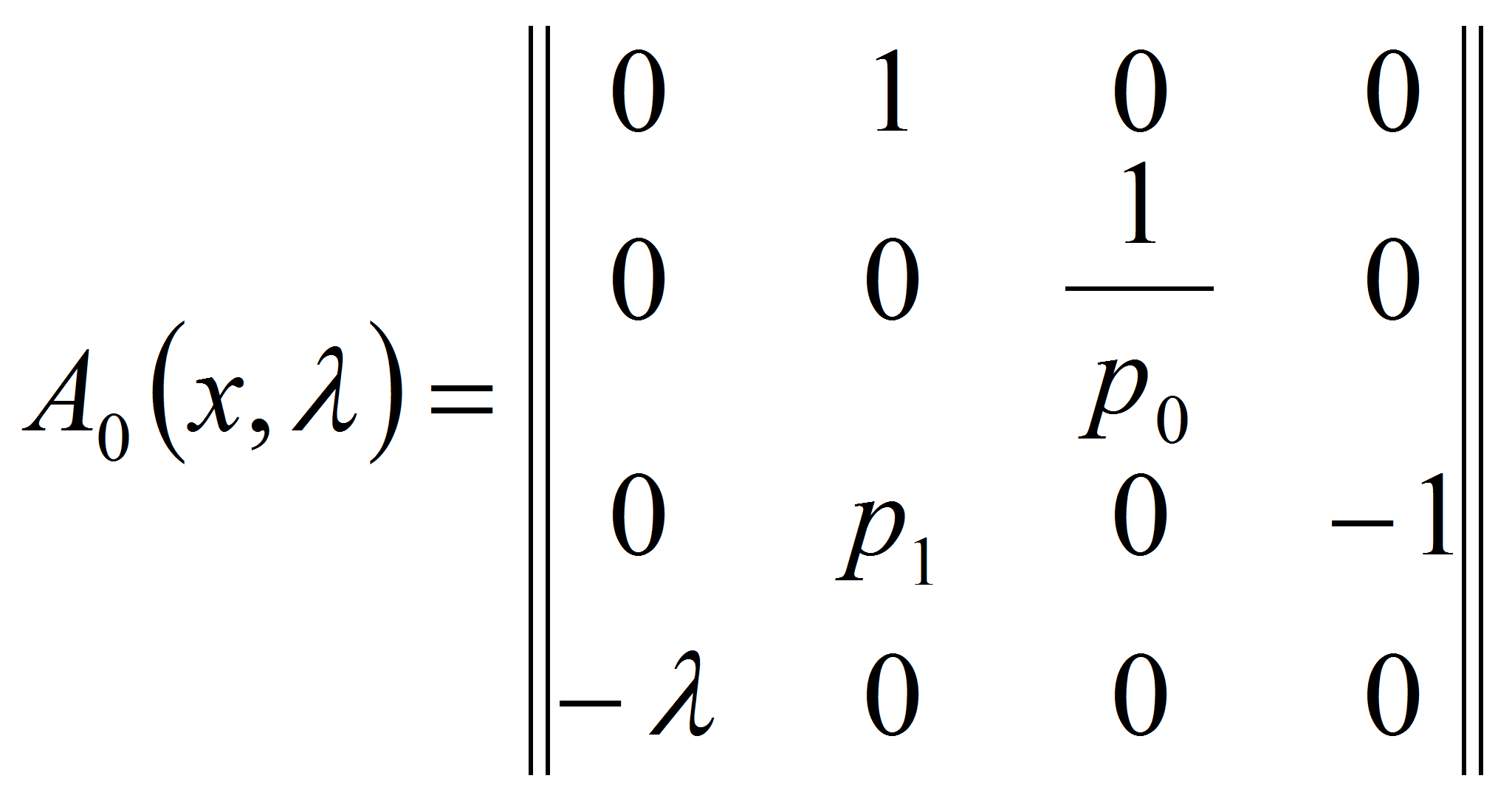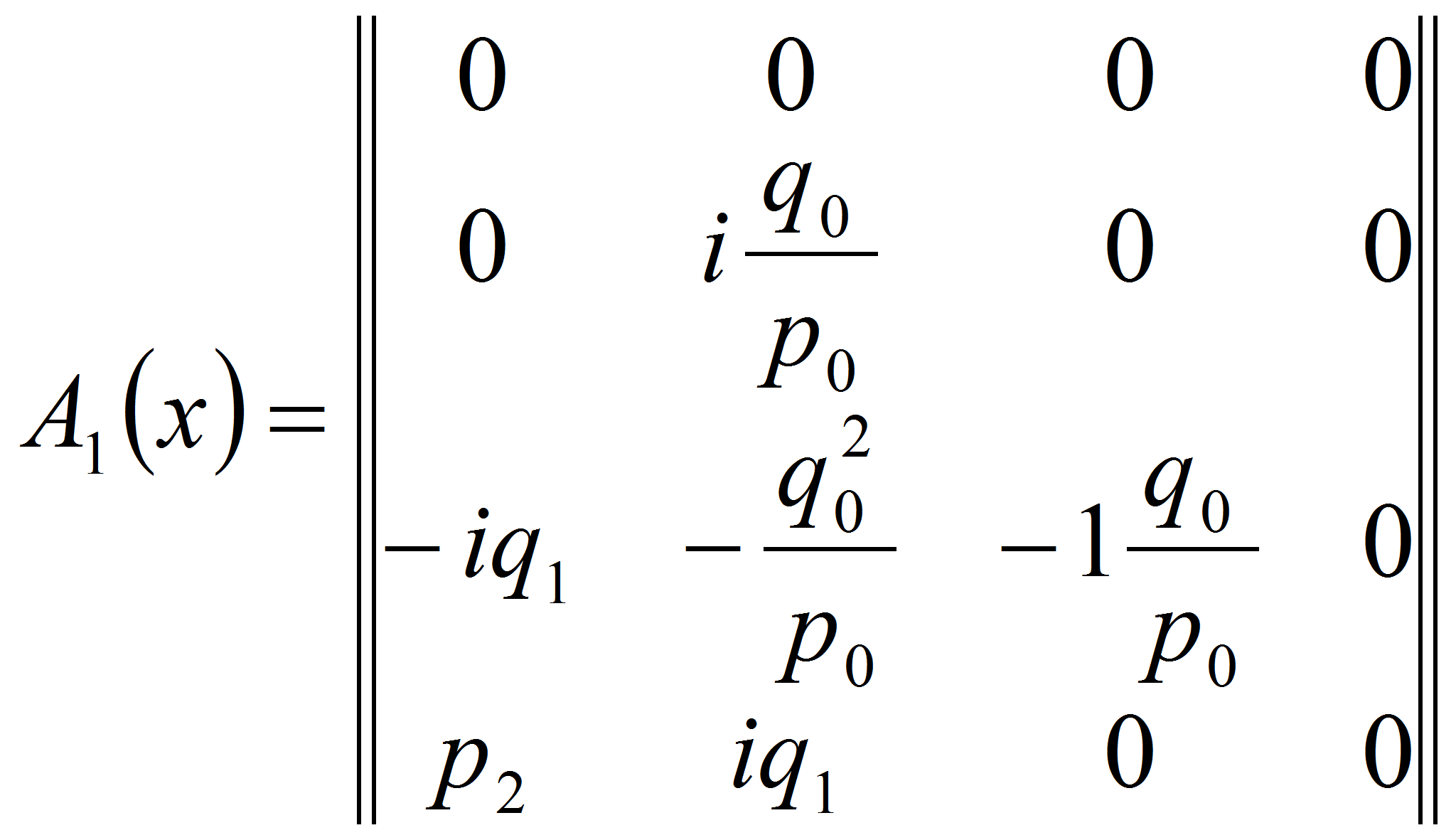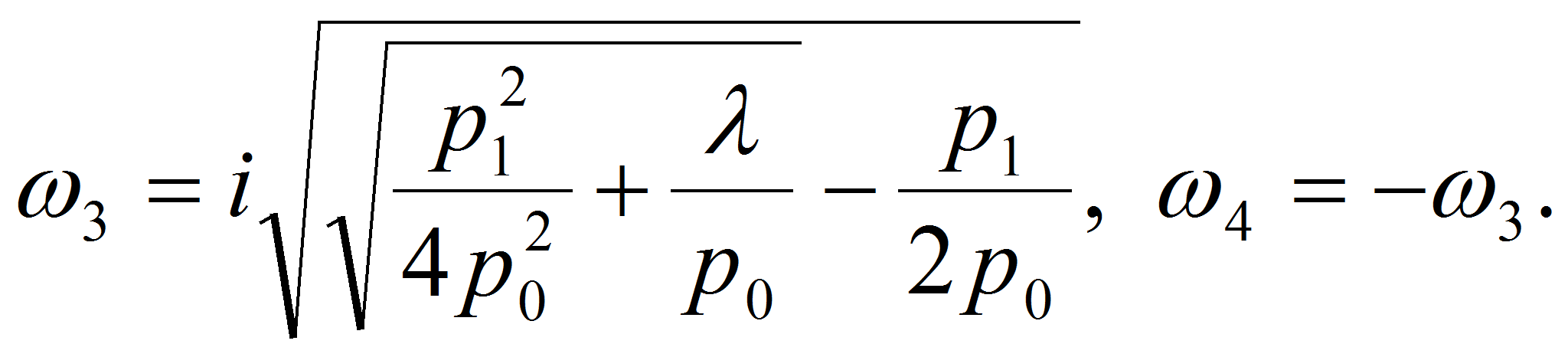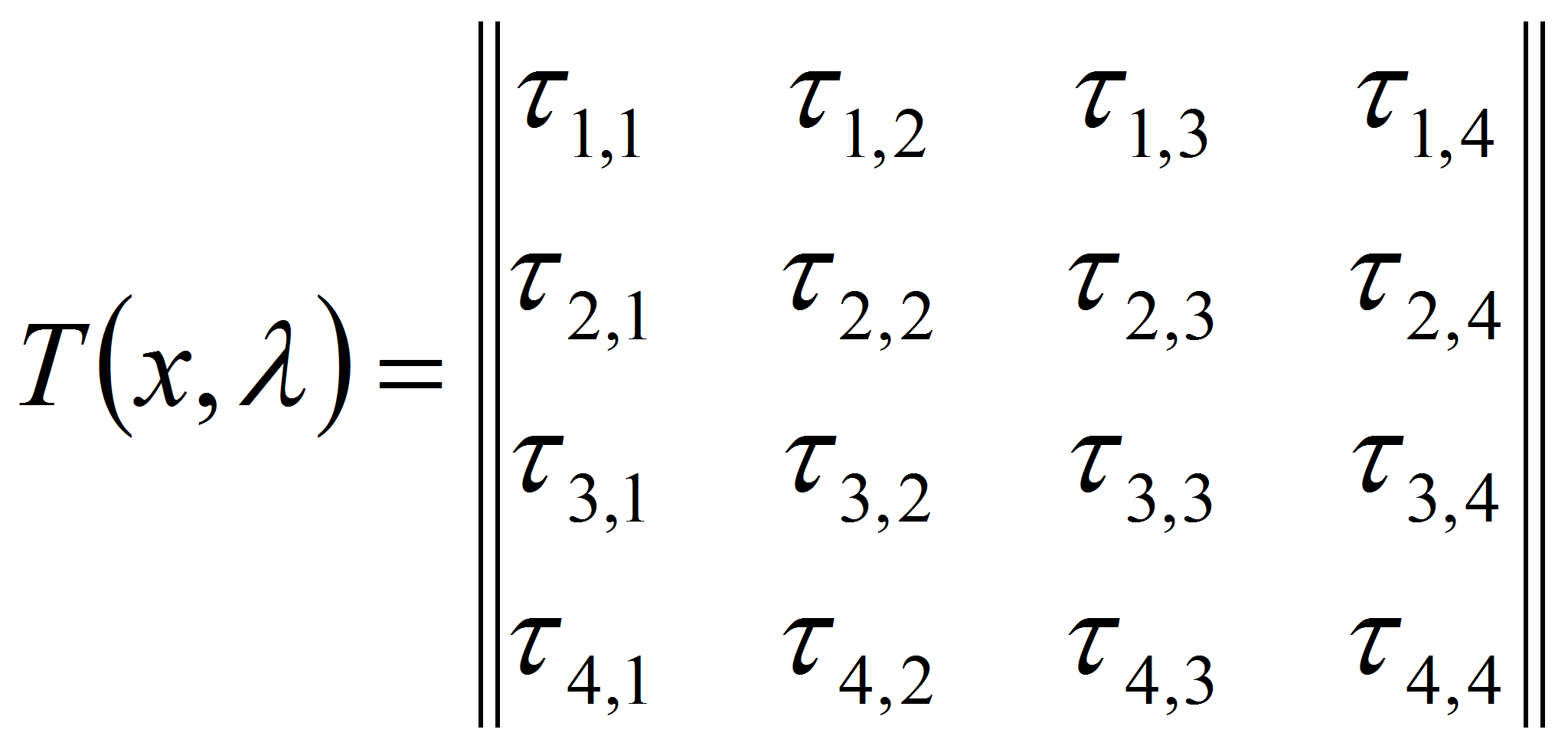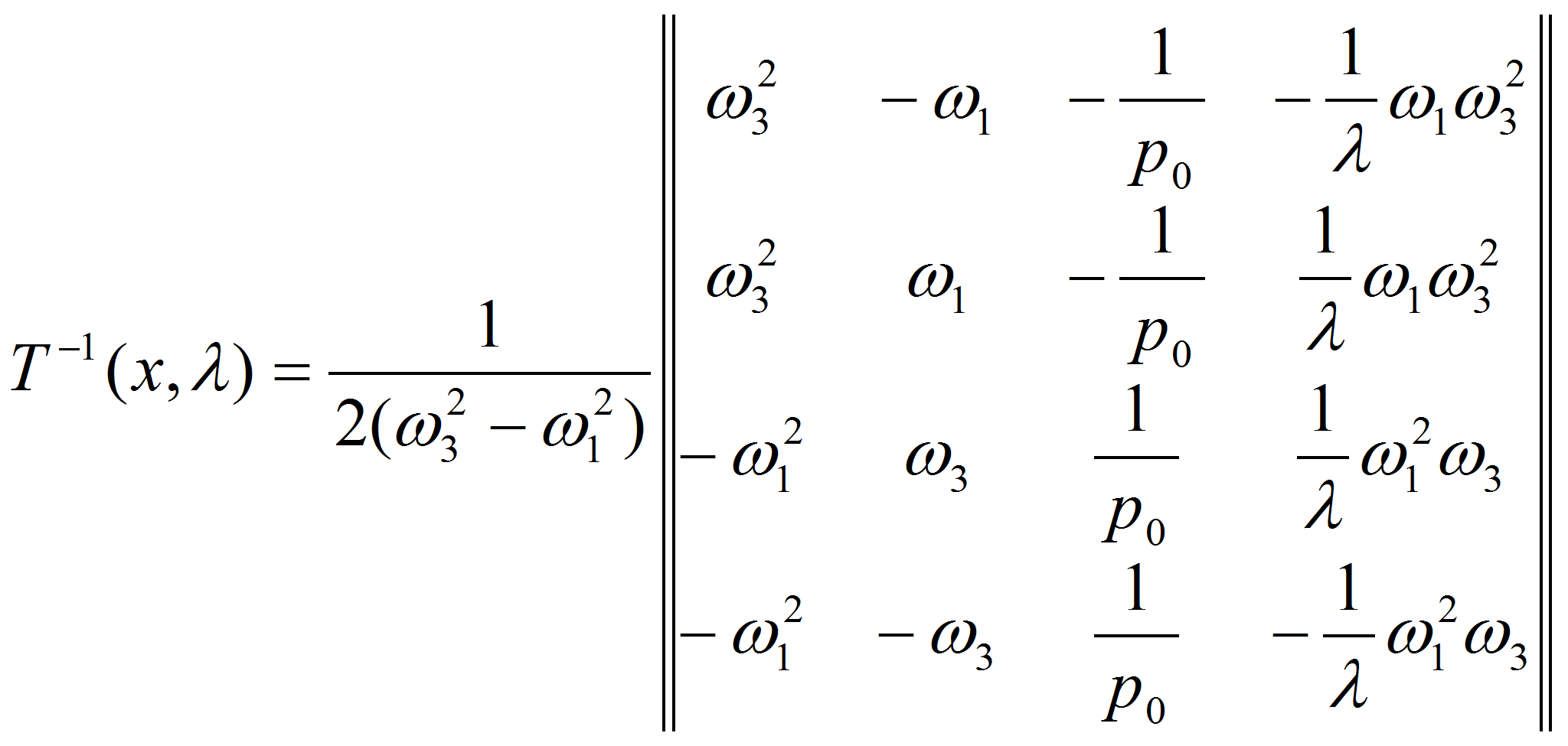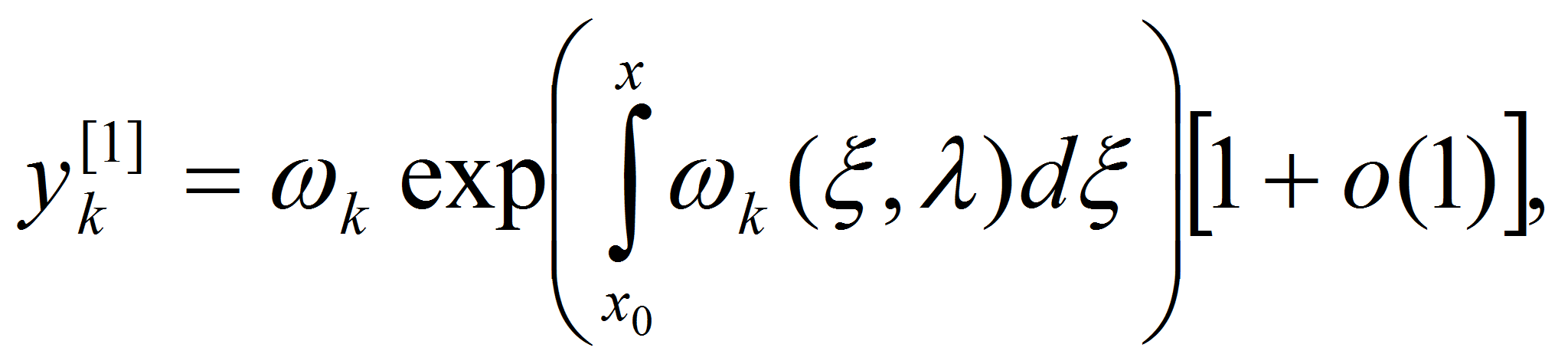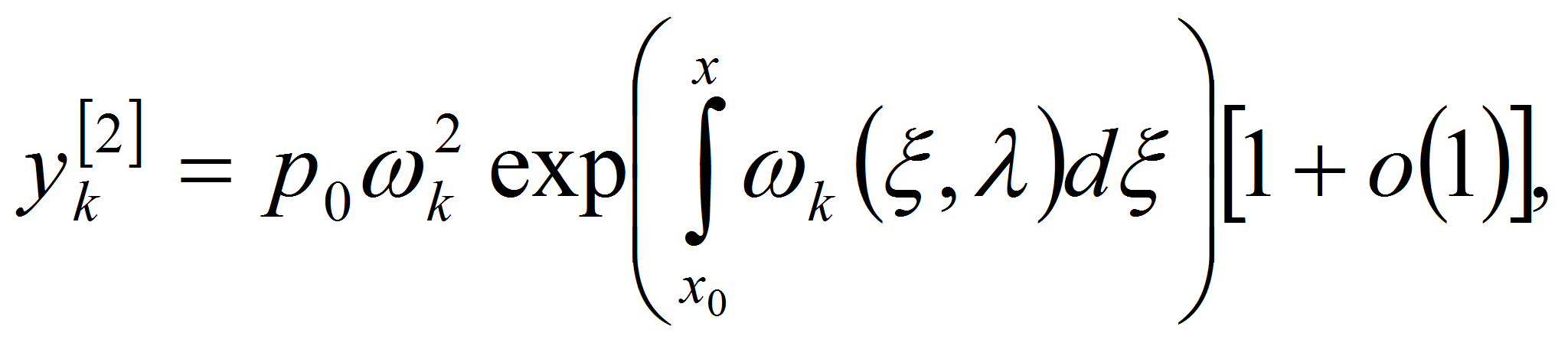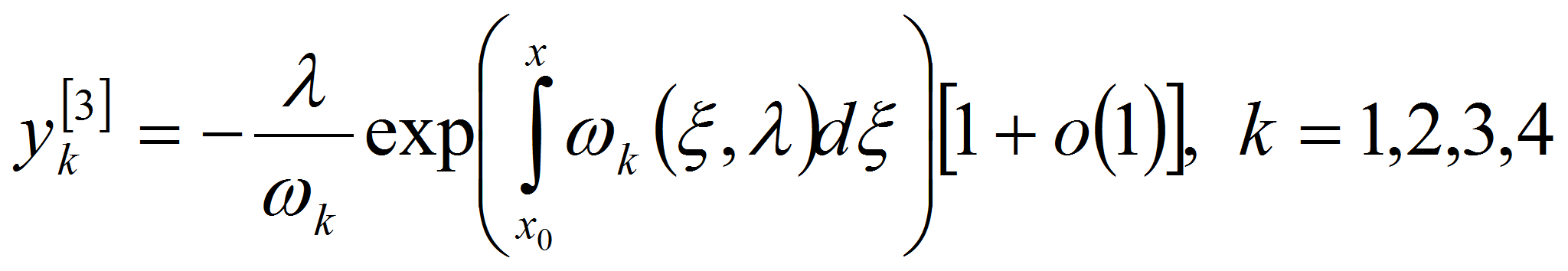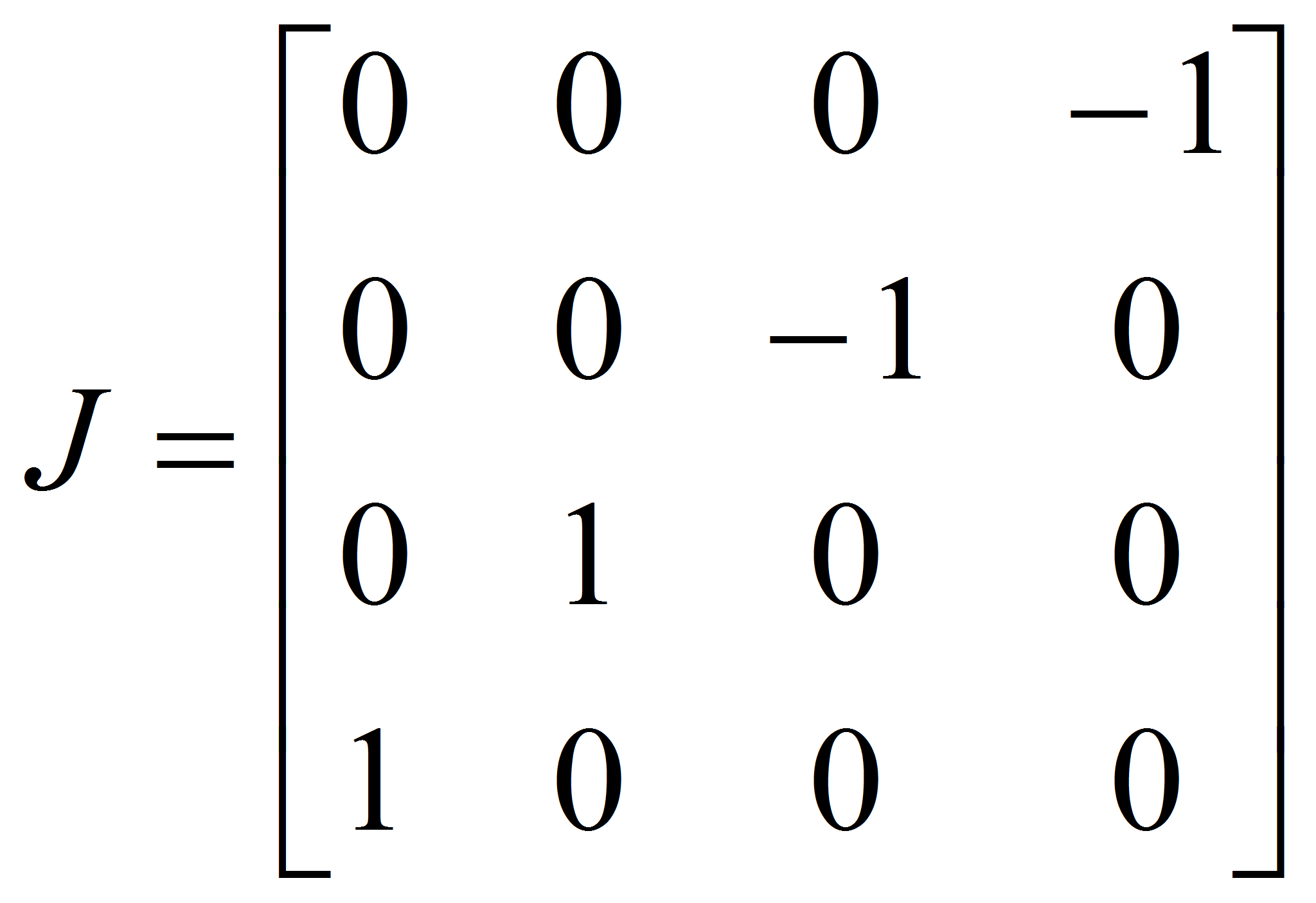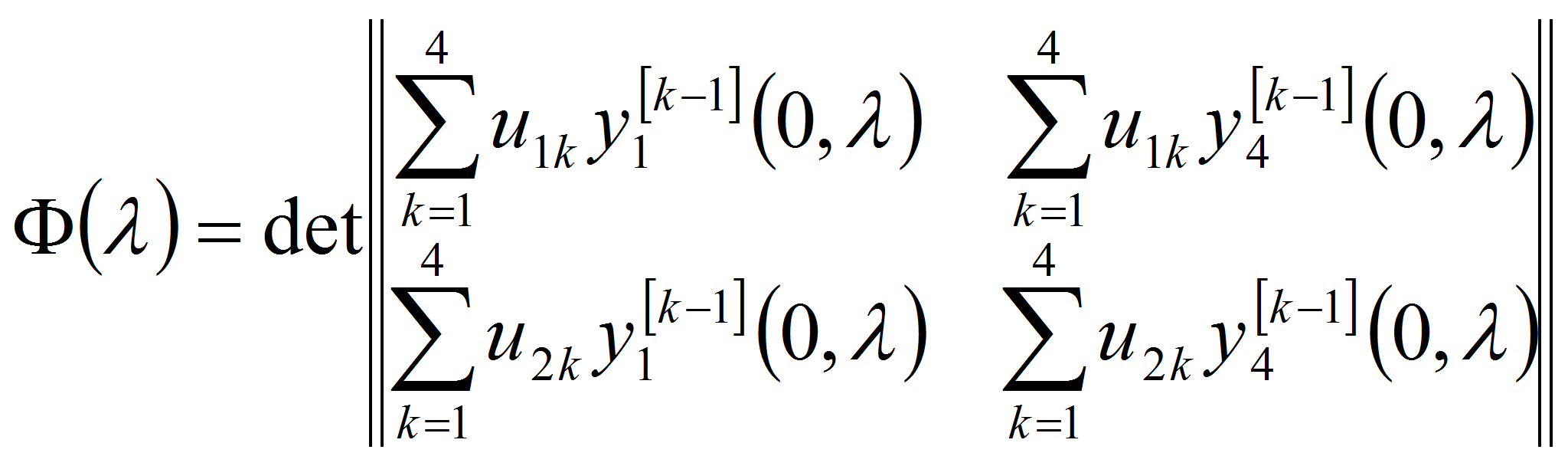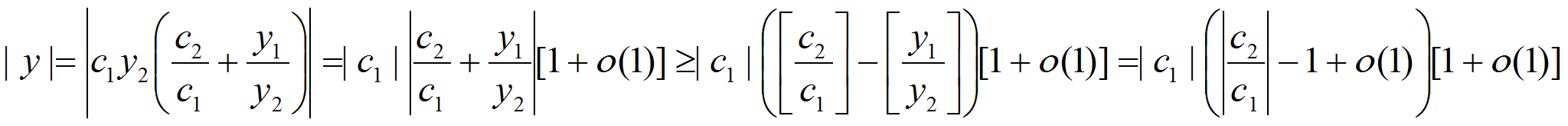При разделении переменных в динамической краевой задаче, описывающей малые колебания неоднородного стержня, жестко закрепленного на правом конце и подвергаемого действию следящей силы на правом конце, возникает спектральная задача четвертого порядка. Спектральные свойства таких задач, вообще говоря, могут отличаться от спектральных свойств аналогичных задач второго порядка. Например, спектр задачи о малых колебаниях стержня в отличие от задачи о малых колебаниях струны может не быть простым. Поэтому результаты, полученные для задач Штурма – Лиувилля, нельзя автоматически применять к задачам четвертого порядка.
Пусть
– формально самосопряженная квазидифференциальная операция
четвертого порядка:
,
где,
- мнимая единица. Операция
задана на полуоси
.
В дальнейшем при некоторых предположениях о поведении коэффициентов
квазидифференциальной операции
найдем
асимптотику решений дифференциального уравнения
,
(1)
когда
.
Установим индекс дефекта минимального симметричного оператора
,
порожденного операцией
в гильбертовом пространстве
;
изучим природу спектра самосопряженного расширения оператора
.
1. Следуя Ф. С. Рофе-Бекетову, определим
квазипроизводные
следующим образом:
.
При этом
.
Теперь сведем уравнение (1) к системе дифференциальных уравнений
первого порядка. Из определения квазипроизводых следует, что
.
Если положить
то уравнение (1) будет эквивалентно системе квазидифференциальных
уравнений
(2)
где
.
Будем считать, что
для всех
а, функции
суммируемы в интервале
,
т.е. их модули медленно меняются на бесконечности. Эти условия на
коэффициенты выражения
,
позволяют получить асимптотические формулы для решений уравнения (1)
и их квазипроизводных по схеме, предложенной в начале 50-х годов
прошлого века И. М. Рапопортом [1] (см. также [2, 3]).
Представим матрицу
в виде суммы двух матриц
и
,
имеющих вид
, 
,
и найдем собственное значение матрицы
,
т.е. корни характеристического уравнения
,
где
- единичная матрица размерности
.
Раскрывая этот определитель, получим уравнение
. (3)
Решая это уравнение, найдем собственные значения матрицы
:
,
Значения корней
выбираются
так, чтобы при положительных значениях
функции
и
принимали вещественные, а функции
и
–
чисто мнимые значения.
Найдем матрицу
такую,
что
(4)
где
- диагональная матрица, диагональными элементами которой являются
собственные значения матрицы
.
Равенство (4) означает, что столбцы матрицы
являются собственными векторами матрицы
,
отвечающими собственным значениям
.
Следовательно, матрица
имеет вид
.
Элементы матрицы
можно найти, решая уравнение
.
Перепишем это уравнение в виде
Следовательно, можно считать, что
Таким образом, матрица
имеет
вид
.
Теперь обычным способом находим обратную матрицу
.
Так как в рассматриваемом случае выполняются все условия теоремы о
преобразовании системы линейных квазидифференциальных уравнений
первого порядка к
– диагональному виду (см., например, [1]), то подстановка
приводит систему (2) к виду
(5)
где элементы матрицы
суммируемы по переменной
в интервале
,
а элементы матрицы
являются непрерывными функциями переменной
.
Если все функции
в интервале
сохраняют знак то система (5) имеет четыре линейно независимых
решения вида
,
-
где
Преобразование
переводит решения
- диагональной системы (5) в некоторые решения системы (2). Учитывая
вид матрицы
,
находим, что решения уравнения (1) и их квазипроизводные
удовлетворяют, если
,
следующим асимптотическим формулам:
(6)
.
2. Найдем индекс дефекта минимального
оператора
,
порожденного дифференциальной операцией
в гильбертовом пространстве
(см., например [4]). Из суммируемости функций
и
на промежутке
следует непрерывность функций
и
,
а также существование пределов
и
.
Тогда, если
,
то из уравнения (3) получим уравнение
, (7)
где
.
Выберем невещественное число
так, чтобы все корни уравнения (7) имели различные вещественные
части. Расположим их по убыванию вещественных частей
.
Так как уравнение (7) содержит только четные степени
,
то одновременно с
его корнем будет также
;
поэтому можно считать, что вещественные части корней
- положительные, а вещественные части корней
- отрицательны. Поскольку функция
непрерывна и
то, начиная с некоторого значения
,
вещественные части
становятся положительными, а вещественные части функций
становятся отрицательными. Отсюда следует, что функции
не принадлежат пространству
,
а функции
принадлежит пространству
.
Докажем, что при
и
. (8)
Действительно,
.
Так как в рассматриваемом случае
,
то из последнего соотношения следует формула (8).
Линейная комбинация вида
не
принадлежит пространству
,
если хотя бы один из коэффициентов
отличен
от нуля. Если
–
первый из коэффициентов
отличный
от нуля, то, устремляя
,
получим
.
Поскольку
,
то и
.
Следовательно,
,
тогда
.
Это значит, что индекс дефекта оператора
есть (2,2). Таким образом, справедлива следующая теорема.
Теорема 1. Если для некоторого
функции
- принадлежат
и
для любых
,
то уравнение (1) имеет четыре линейно независимых решения
,
которые удовлетворяют, установленным выше, формулам (6).
Индекс дефекта оператора
есть (2,2).
Пусть
- самосопряженное расширение оператора L0.
Так как индекс дефекта оператора L0
есть (2,2), то самосопряженный оператор
определяется системой краевых условий в точке
,
которые, следуя А.В. Штраусу, можно представить в виде
,
(9)
где
- некоторая прямоугольная матрица, состоящая из двух строк и четырех
столбцов, такая что
,
где
.
Пусть
.
Найдем собственные значения самосопряженного оператора
,
расположенные на отрицательной полуоси
Соответствующая собственная функция
должна принадлежать
и поэтому, при соответствующей нумерации
,
является линейной комбинацией функций
и
,
т. е.
.
Кроме того, собственная функция
должна удовлетворять условию (9), которое теперь можно представить в
виде
.
(10)
Эта система имеет нетривиальное решение относительно
и
тогда и только тогда, когда обращается в нуль определитель
.
Пусть
- нуль этого определителя. Тогда соответствующая собственная функция
оператора
представима формулой
,
в которой содержатся коэффициенты
,
являющиеся нетривиальными решениями системы (10) соответствующими
.
Кратность собственного значения
определяется рангом матрицы определителя
в точке
.
То, что отрицательные
,
не совпавшие ни с одним из собственных значений оператора
,
не принадлежат спектру этого оператора, следует из ограниченности при
этих l резольвенты оператора
,
где
-
тождественный оператор.
Пусть
- симметрический квазидифференциальный оператор с индексом дефекта
,
а
- его самосопряженное расширение. Если при некотором вещественном
значении спектрального параметра
его дефектное число
оператора
меньше
,
то
принадлежит спектру самосопряженного оператора
.
Если, кроме того,
не является собственным значением оператора
,
то
принадлежит непрерывной части спектра оператора
.
Пусть теперь
.
В этом случае
,
а функции
,
не принадлежат
.
Более того, никакая нетривиальная линейная комбинация
не принадлежит
Действительно, если,
то
.
Если
,
то функция
имеет вид
.
Предположим, что
тогда получим
и поэтому функция
не принадлежит пространству.
В этом случае, когда
,
требуемое соотношение можно получить, используя
ограниченность сверху при любом фиксированном
функции
.
Теорема 2. Если коэффициенты дифференциального выражения
удовлетворяют условиям:
,
то непрерывная часть спектра самосопряженного оператора
заполняет всю положительную полуось
,
а на отрицательной полуоси
может находиться только дискретная часть спектра самосопряженного
оператора
.
Замечание. В случае, когда коэффициенты
тождественно равны нулю, получаем хорошо известную ситуацию
суммируемых коэффициентов.
- Литература:
- Рапопорт И.М. О некоторых асимптотических методах в теории дифференциальных уравнений. – Киев: Изд-во АН УССР, 1954.
- Everitt W. N. Fourth order singular differential equations // Math. Ann. – 1963. – V. 149. – P. 230 – 340.
- Наймарк М. А. Линейные дифференциальные операторы. – М.: Наука, 1969. – 526 с.
- Плеснер А.И. Спектральная теория линейных операторов. – М.: Наука, 1965. – 624 с.
