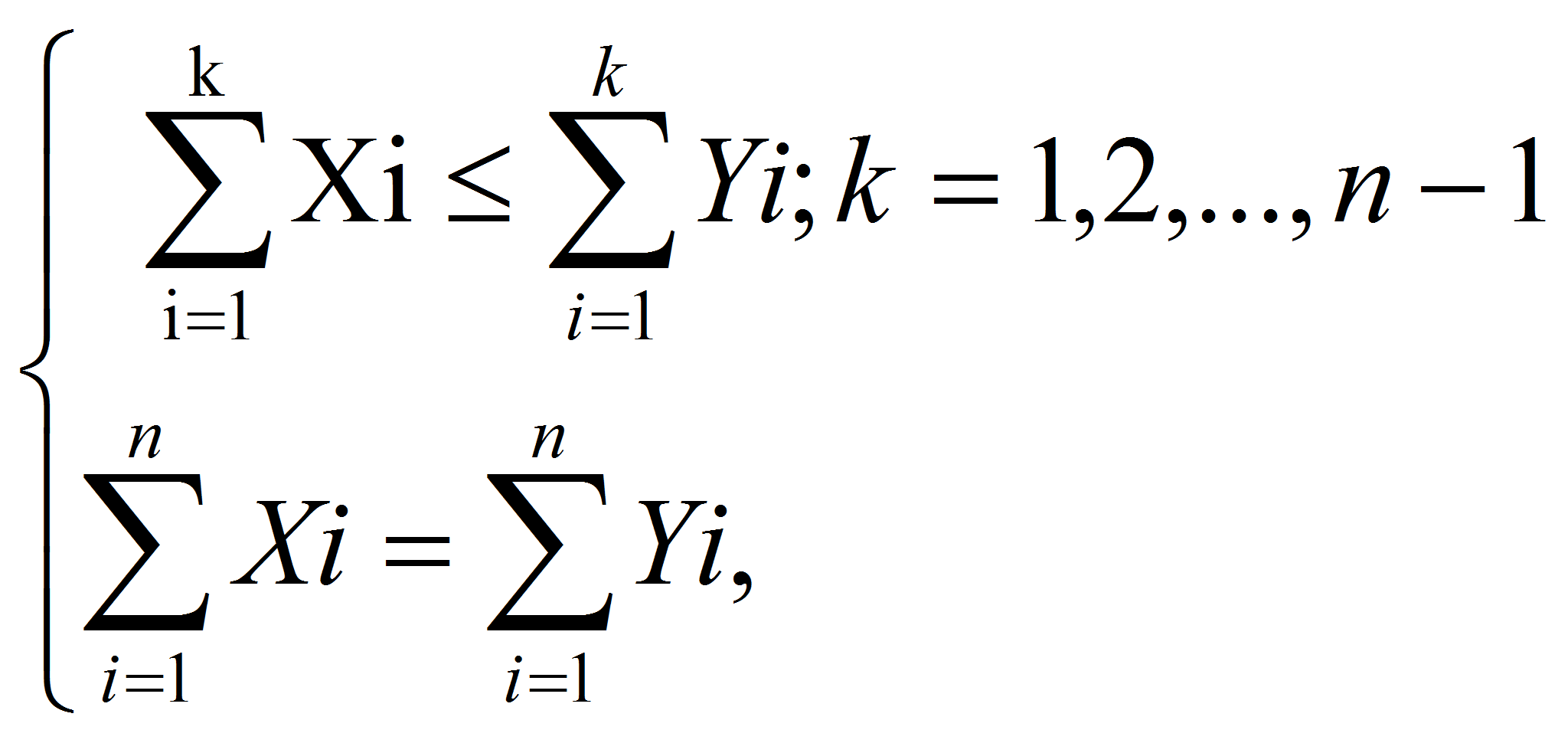Часто на олимпиадах различного уровня требуется применение классических неравенств для оценки каких-то величин. Это неравенства: Коши, Миньковского, Гёлдера, неравенство Эрдёша-Морделла и другие. В приведенной работе освещён материал, как при помощи леммы доказать неравенство Эрдёша-Морделла, кроме того показано применение неравенства Эрдёша-Морделла для доказательства других неравенств, встречающихся в задачах алгебры, геометрии.
Глава I. Вариация на тему неравенство Эрдёша-Морделла
В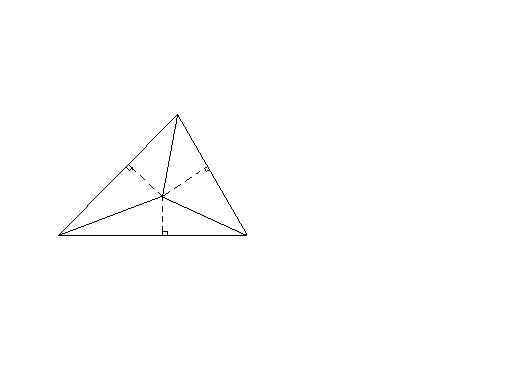
ведём
обозначения, которые мы будем использовать в дальнейшем.
-
С
- V U
- M
- А B
- W
Пусть дан ABC. Его стороны обозначим через a, b и c.
Пусть M – произвольная точка, расположенная внутри ABC.
Тогда MA = Ra, MB = Rb, MC=Rc.
Опустим из точки M перпендикуляры на стороны треугольника (рис.1).
Пусть MU = q( M, BC ) = da, MV = q ( M, AC ) = db и MW = q ( M, AB ) = dc.
В настоящее время известно несколько десятков различных неравенств, связывающих величины Ra, Rb, Rc и da, db, dc. Рассмотрим некоторые из них.
Наиболее известным из таких неравенств является неравенство Эрдёша-Морделла. Оно имеет довольно длинную историю. В 1935 году известный венгерский математик Пол Эрдёшь выдвинул предположение о том, что справедливо неравенство:
Ra+Rb+Rc 2(da+db+dc),но доказать его не смог. Первым доказать это неравенство удалось английскому математику Л.Дж. Морделлу, однако его доказательство существенно использовало тригонометрию и было довольно сложным.
И лишь в 1940-50-ых годах усилиями многих известных математиков были найдены простые доказательства неравенства Эрдёша – Морделла.
2.1. Прежде, чем перейти к доказательству неравенства Эрдёша–Морделла, сформулируем и докажем лемму, которая понадобиться нам в дальнейшем.
Лемма
aRa cdc+bd
Доказательство:
П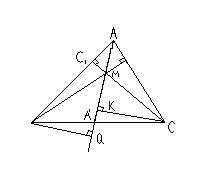
остроим
BQAM
и CKAM
(рис.2).
-
- В1
- В
- В1
Очевидно, что a=BC=BA1+A1C BQ + CK (это следует из того, что в прямоугольном
треугольнике гипотенуза больше любого из катетов).
Значит, aRa=BCAM BQAM + CKAM=2SAMB+2SAMC=cdc+bdb.
Аналогично доказывается, что
bRb ada+cdc, (11)
cRc ada+bdb. (111)
Замечание: при доказательстве мы использовали только то, что точка M лежит внутри угла BAC, а не то, что точка M лежит внутри треугольника.
Как нетрудно видеть, каждое из неравенств (1), (11), (111) обращается в равенство только в том случае, когда точка M принадлежит соответствующей высоте (ha,hb и hc соответственно).
Уже доказанная нами лемма позволяет получить ряд неравенств, связывающих величины Ra, Rb, Rc и da, db, dc.
А. Сложим неравенства (1),(11) и (111).
Получим неравенство:
aRa+bRb+cRc 2(ada+bdb+cdc) ( 2 ).
Равенство здесь достигается, когда AMBC, BMAC, CMAB (см. рис. 1), т.е. точка M совпадает с ортоцентром ABC.
B. Перемножим неравенства (1), (11), (111), получим:
aRabRbcRc (ada+bdb)( bdb+cdc)( ada+ cdc).
Но согласно неравенству между среднем арифметическим и средним геометрическим двух положительных чисел
сdc + bdb 2(cdc bdb),
ada + cdc 2(ada cdc),
ada + bdb 2( adabdb).
Перемножив эти неравенства, получим
aRabRbcRc 8adacdc bdb
RaRbRc8dadcdb
Знак равенства здесь имеет место, если BC = BA1 + A1C=BQ + CK, т.е. если AMBC и также BMAC, CMAB, т.е. если M является ортоцентром ABC и, кроме того, ada = cdc = bdb или SMBC =SMAC =SMAB, т.е. точка М является центром тяжести ABC. Но если ортоцентр и центр тяжести ABC совпадают, то ABC равносторонний (и точка Ь совпадает с его центром).
2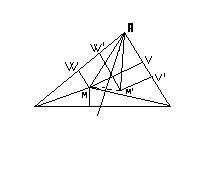
.2.
Неравенство Эрдёша-Морделла.
- Одно из самых простых и красивых из числа известных мне доказательств основано на применении сформулированной выше леммы.
B C
- U l
Применим неравенство леммы к точке М1, симметричной к точке М относительно биссектрисы l BAC (это правомерно ввиду замечания после доказательства леммы). Действительно, в силу симметрии Ra1 = M1A= MA = Ra, db1=M1V1=NW=dc, dc1=M1W1=MV=db (рис.3). Получим:
Ra(c/a)db+(b/a) dc
Аналогично,
Rb(c/b) da+(a/b) dc и
Rс(a/c) db+(b/c) da
Складывая эти неравенства, получим:
Ra + Rb + Rc (b/c + c/b) da + ( a/c + c/a) db + (b/a + a/b) dc 2(da + db + dc)
в силу известного неравенства: x>0, y>0, x/y+y/x 2
Знак равенства имеет место лишь в том случае, если b=c, a=c и a=b, т.е. если ABC равносторонний и если, кроме того, AMBC, BMAC, т.е. М совпадает с центром правильного ABC.
Приведём доказательства ещё двух неравенств, связывающих величины Ra, Rb, Rc и da, db, dc.
Д.
Ra Rb Rc (da+db) (da+dc) (db+dc), (4)
Доказательство:
Согласно лемме, для любой точки М внутри BAC
Ra a сdc + bdb ( * )
Применяя это неравенство к точке М1, симметричной к точке М относительно биссектрисы А, получим:
aRaсdb + bdc ( * * )
(см. докозательство неравенства Эрдёша-Морделла).
Сложим ( * ) и ( * * ), получим:
2aRaсdb + bdc + сdc + bdb =(b+c) ( db+dc)
Аналогично устанавливается , что
2bRb(a+c)(da+dc) и
2с Rс(a+b)( da+db)
Перемножим три последних неравенства, получим:
8abc RaRb Rс(a+b)(b+c)(c+a)( da+db) (da+dc) ( db+dc).
Но в силу неравенства между средним арифметическим и средним геометрическим
a+b 2(ab),
a+c 2(bc),
b+c 2(ac).
Поэтому
8abc RaRb Rс2(ab) 2(bc) 2(ac) (da+db) (da+dc) ( db+dc)= 8abc(da+db) (da+dc)
( db+dc), т.е. RaRb Rс(da+db) (da+dc) ( db+dc), что и требовалось доказать.
Равенство имеет место, лишь, если a=b, b=c, т.е. a = b = c, а значит, ABC – правильный, и, кроме того, (как было показано выше) точка M совпадает с точкой пересечения высот ABC, т.е. с центром этого треугольника.
Е. Справедливо также неравенство
RaRb + RbRc + RaRc4(dadb + dadc+ dbdc) (5)
Его доказательства мы здесь не приводим, его можно найти, например в [I] (решение задачи 116 в).
Неравенства ( 4 ) и ( 5 ) принадлежит А. Оппенгейму.
Как следует из [I], Оппенгейм предположил, что справедливо следующее неравенство, родственное неравенству ( 4 ) и более сильное, чем неравенство (5):
RaRb + RbRc + RaRc(da+db) (da+dc) + (da+db) ( db+dc) + (da+dc) ( db+dc) (6)
Однако неравенство это, как будто, никем пока не доказано (и не опровергнуто) [I, стр. 58].
Глава II. Понятие мажоризации
Ниже я приведу полученное мной доказательство неравенства (6). Несмотря на то, что найденное мной доказательство не вполне элементарно (хотя, на мой взгляд, доступно школьнику старших классов), оно иллюстрирует довольно мощный единый подход к исследованию неравенств, основанный на методе мажоризации.
Настоящий реферат не ставит перед собой цель изложить метод мажоризации. Ему посвящено большое количество литературы, в частности. Я приведу лишь те определения и теоремы, которые будут использоваться непосредственно [II].
Определение: Пусть x
и y – наборы из n действительных чисел, x=(x1,x2
…,xn),
y=(y1,
y2,…,yn).
Полагаем, что x
wy,
если
; k=1,2,…,n.
В этом случае говорят, что у слабо мажорирует х или х слабо супермажорирует у.
Будем считать, что в АВС с b a.
Проверим, что в наших обозначениях
(Ra,
Rb,
Rc)
w(da+db,
da+dc,
db+dc), (7)
Для этого нам надо проверить выполнение неравенств:
Ra db+dc
Ra+ Rb da + db + 2dc
Ra+Rb+Rc 2(da + db + dc) (8)
Тогда в силу леммы:
Ra
dc+
db
db+dc,
Тем самым проверенно выполнение первого неравенства из (8)
Складывая неравенства
Ra
db+
dc
Rb
da+
dc,
полученные в ходе доказательства неравенства Эрдёша-Морделла, получим:
Ra+
Rb
da+
db
+(
+)dc
(здесь мы вновь использовали неравенство x>0,
y>0,
x/y+y/x
2).
Итак, второе неравенство из (8) также проверено.
Третье же неравенство представляет собой не что иное, как неравенство Эрдёша-Морделла, доказанное ранее.
Нам понадобиться
Теорема. ( [II], стр.68).
Вещественная функция , определённая на множестве АRn, удовлетворяет условию
(xwy
на А) (х)
(у),
тогда и только тогда, когда монотонно не убывает и S – вогнута1) на А.
Пример S – вогнутых
на
2)
функций дают так называемые элементарные симметрические
функции.
Sk(x) – k-я элементарная симметричная функция от переменных
x1, x2,…,xn. Таким образом,
S0(x)≡1,
S1(x)=
,
S2(x)=
,…,
Sn(x)=
Относительно элементарных симметричных функций справедливо
Примечание
1)Если х, у Rn ={( x1, x2,…,xn):xiR для всех i} и
то говорят, что у
мажорирует х и пишут xy.
Определение ( [ II], стр. 62)
Вещественная функция ,
определенная на множестве АRn,
называется S – вогнутой на А, если ( xy
на А ) (х)
(у).
2)
={(
x1, x2,…,xn):xi
0
для всех i}
Предложение: Функция
Sk монотонно неубывающая и S –
вогнутая на
Это предложение принадлежит Шуру, доказательство его приведено, например в [II] (стр. 88).
Теперь мы сформулировали все необходимые определения и теоремы, касающиеся метода мажоризации.
Для набора положительных действительных чисел х1, х2, х3 существуют три элементарные симметрические функции, не равные тождественно константе:
S1(x)= х1 + х2 + х3,
S2(x) = x1x2+x2x3+x3x1,
S3(x)=x1x2x3.
Теперь применим сформулированную выше теорему к наборам
(Ra,
Rb,
Rc)
w(da+db,
da+dc,
db+dc),
и функциям S1(x),
S2(x),
S3(x)
(в силу сформулированного выше предложения все три они монотонно
неубывающие и S – вогнутые на
).
1. Для S1(x) имеем:
Ra+Rb+Rc da + db + dc + da + db + dc
Ra+Rb+Rc 2(da + db + dc), т.е. получили неравенство Эрдёша-Морделла, которое сразу следовало из произведенного упорядочения.
2. Для S2(х) получим:
RaRb + RbRc + RaRc(da+db) (da+dc) + (da+db) ( db+dc) + (da+dc) ( db+dc),
т.е. получили приведенное выше неравенство Оппенгейма ( 6 ).
3. Для S3(х) получаем:
RaRb Rс(da+db) (da+dc) ( db+dc),
т.е. получили доказанное выше другим способом неравенство (4), также принадлежащее Оппенгейму.
Т.к. все три полученных неравенства являются симметричными относительно a, b, c, то из полученного нами доказательства для случая сba следует, что все эти три неравенства доказаны для произвольных значений a, b, c.
Так что, оказывается, неравенства (4) и (6) родственны не только по внешнему виду.
Оба они оказываются следствием одной теоремы об элементарных симметрических функциях.
- Литература:
- Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Геометрические неравенства и задачи на максимумы и минимумы. Математическая наука, 2000 год.
- Маршалл А., Олкин И. Неравенства: теория мажоризации и ее приложения: перевод с английского. М. Мир, 2005 год.