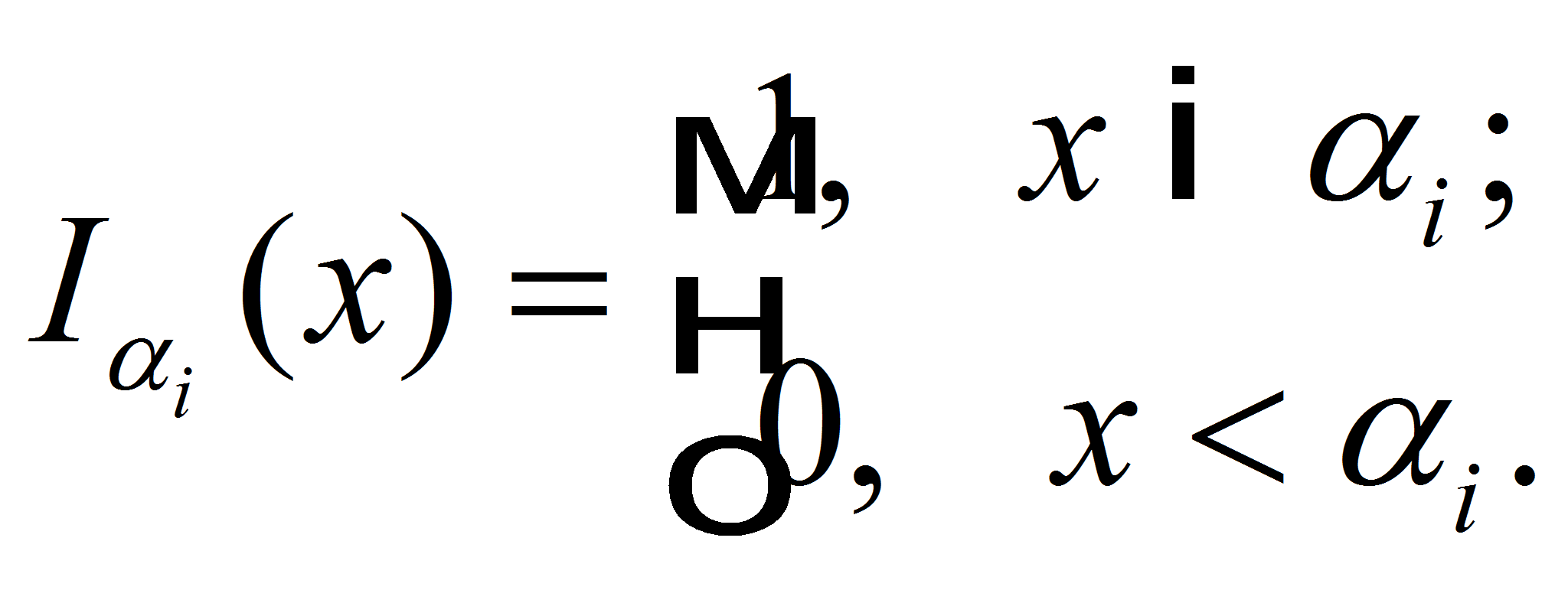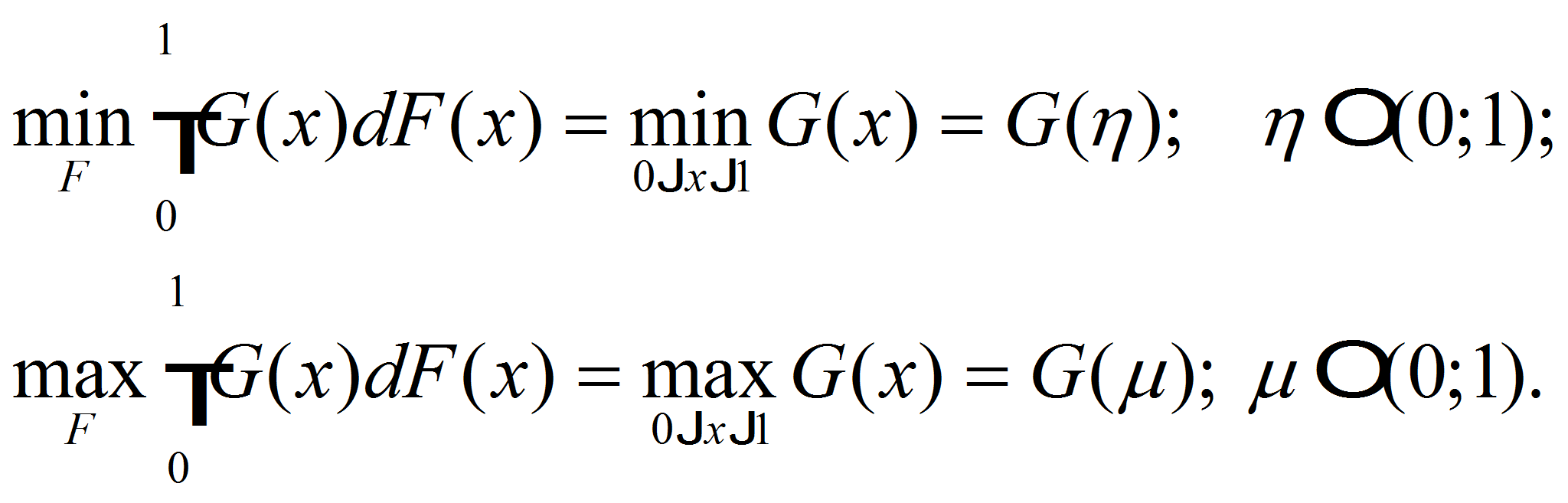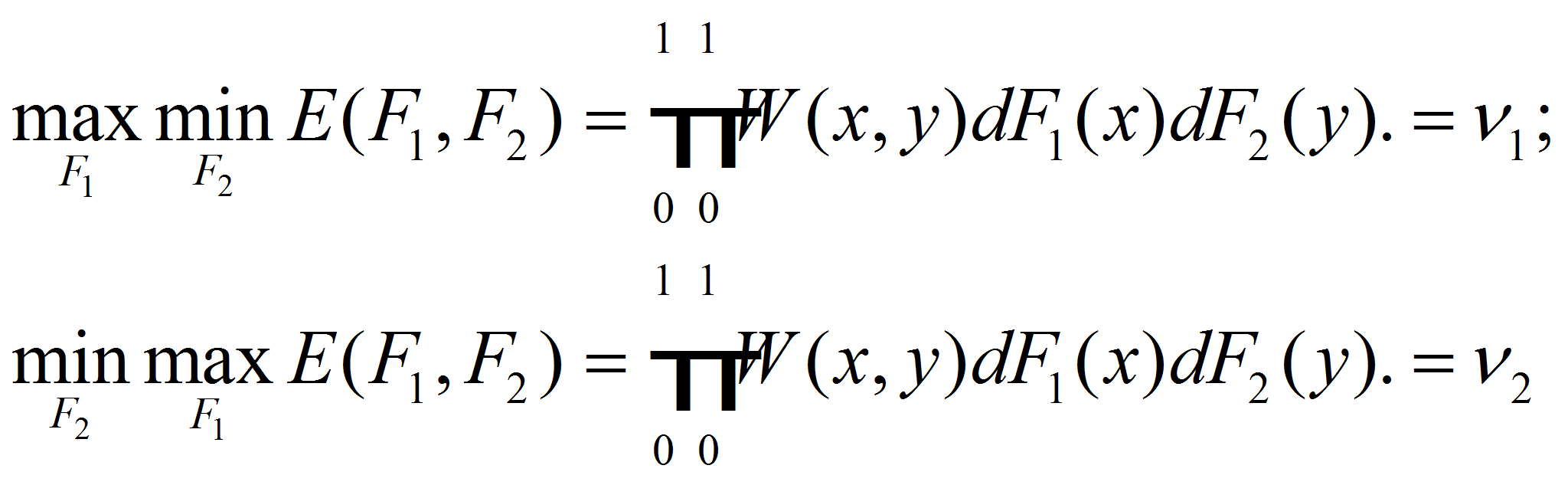Современная производственная и военно-техническая деятельность связана с выбором таких решений, которые позволили бы получить некие оптимальные результаты — затратить минимум средств, достичь максимальную прибыль, наилучших показателей и т.д. Но чтобы что-то рассчитать, надо формализовать задачу, т. е. составить математическую модель изучаемого явления, поскольку математические методы можно применять не к непосредственно изучаемой деятельности, а лишь к моделям того или иного типа объектов. При представлении конфликтной ситуации в военном деле возникает ряд трудностей в связи с описанием правил, условий, игроков, стратегий, ходов и выигрышей, т.е. в описании математической модели предстоящего конфликта по сценарию «если-то». Задача заключается в том, чтобы данную конфликтную ситуацию по возможности привести к формализованной игре без значительных потерь реальных целей, найти метод решения, провести расчеты и анализ.
Результаты исследований математических моделей представляют практический интерес только тогда, когда модели адекватно отображают реальные ситуации. Даже в тех случаях, когда принятие решения, казалось бы, полностью автоматизировано (например, в процессе автоматического управления предприятием или космическим объектом), роль человека не устраняется, ибо, в конечном счете, от него зависит выбор алгоритма, по которому осуществляется управление.
В теории игр рассматриваются вопросы о выборе оптимальных стратегий в различных конфликтных ситуациях. Данная тема является актуальной и недостаточно изученной в применении к практическим задачам военно-технического комплекса, экономике, управлении, юриспруденции, политике и т.д. С помощью теории игр для нескольких бескоалиционных противников (или противоборствующих сторон) определяются стратегии, которые приведут если не к положительному выигрышу, то, по крайней мере, к наименьшим потерям. В условиях конфликта принимающему решение необходимо учитывать не только свои собственные интересы, но и цели и интересы противника, которые в общем случае неизвестны. Таким образом, возникает достаточно непростая ситуация выбора оптимального действия для каждого из участников конфликтной ситуации.
Такой анализ является более неопределенным в смысле законов, предсказаний и логики и имеет вероятностный характер. Поэтому моделирование с тщательно подобранными реалистическими деталями не может дать общего достоверного результата, если опыт проведения операции не будет повторен очень большое число раз. С точки зрения дифференциальных игр единственное, на что можно надеяться, – это на подтверждение заключений теории. Особенно важно случай, чтобы такие заключения были выведены из упрощенной модели.
Заинтересованные стороны называют игроками. Любое возможное для игрока действие в рамках заданных правил игры называется его стратегией. В условиях конфликта каждый игрок выбирает свою стратегию, в результате чего складывается набор стратегий, называемый ситуацией. Заинтересованность игроков и ситуации заключается в том, что каждому игроку в каждой ситуации приписывается число, выражающее степень удовлетворения его интересов в этой ситуации и называемое его выигрышем. Протекание конфликта состоит в выборе каждым игроком своей стратегии и получении им в сложившейся ситуации выигрыша. Одной из плодотворных форм воплощения представлений об оптимальности можно считать понятие равновесия, при котором складывается такая равновесная ситуация, в нарушении которой не заинтересован ни один из игроков.
В некоторых практически
важных ситуациях рассматриваются бесконечные игры, в которых
участники конфликта производят выборы из бесконечных множеств.
Предположим, что игрок (стратег)
выбирает элемент
из
а игрок
выбирает элемент
из
Тогда игрок
платит игроку
сумму
Для фиксированного выбора второго игрока стратегии
выигрыш первого определяется функцией
(1)
Предположим теперь, что
игрок
применяет случайный
механизм, которому соответствует функция распределения
Для выбора между различными типами функций распределения необходимо
определить математическое
ожидание
полученного выигрыша. Для этого рассмотрим разбиение интервала
точками
Мы предположили для определенности, что все значения
(также как и
)
берутся из единичного отрезка
Очевидно, что для достаточно хорошей функции
с помощью интегральной суммы вида
(2)
где
можно сколь угодно близко подойти к выигрышу первого игрока. Эта
сумма является обобщением аналогичной суммы для обычного риманова
интеграла
когда
Предел интегральной суммы (2), если он существует и не зависит от
выбора значений
по
определению есть интеграл
Стильтьеса
функции
по
и
обозначается
(3)
Таким образом, математическое ожидание выигрыша первого игрока равно
(4)
Вследствие сложного
предельного перехода интеграл Стильтьеса не всегда существует
(например, если функции
и
имеют
общую точку разрыва). Справедлива следующая теорема.
Теорема.
Если функция
непрерывна на отрезке
а функция
является монотонной, то интеграл Стильтьеса (3) существует.
Если интегралы, стоящие в
обеих частях равенства (5), существуют и функция
имеет производную в каждой точке заданного интервала, то задачу
вычисления интеграла Стильтьеса можно свести к нахождению обычного
риманова интеграла по формуле
(5)
Рассмотрим случай, чаще всего возникающий при решении такого р задач, когда функция распределения является линейной комбинацией ступенчатых функций, т.е.
(6)
где через
обозначили единичные функции-ступени типа функции Хевисайда, имеющие
скачки соответственно в точках
т.е.
(7)
Очевидно, что функция
также является ступенчатой и имеет число разрывов не больше
суммарного числа разрывов функций
Сформулируем теорему, позволяющую вычислять интеграл Стильтьеса по
ступенчатой функции
.
Теорема.
Для любых
вещественных чисел
удовлетворяющих неравенствам
и ступенчатой функции распределения
вида (6) интеграл Стильтьеса можно найти по следующей формуле:
(8)
Здесь
-
любая определенная на отрезке
функция, непрерывная в точках
Если
-
непрерывная на данном отрезке функция, то она достигает своего
максимального и минимального значения. Они определяются по формулам
(9)
Аналогичным образом с
помощью интеграла Стильтьеса находится цена непрерывной игры и
оптимальная смешанная стратегия для обоих игроков-стратегов.
Предположим, что
есть платежная функция (или функция выигрыша) непрерывной игры и
игрок
выбирает стратегию
согласно функции распределения
игрок
выбирает стратегию
с функцией распределения
Тогда для
любой выбранной вторым игроком стратегии
математическое ожидание выигрыша для первого игрока равно
(10)
Справедливо следующее
утверждение. Если платежная функция
-непрерывная
функция двух переменных в единичном квадрате, то величины
(11)
существуют и равны между
собой. В этом случае их общее значение
определяет
цену игры для первого стратега и существует седловая точка
определяющая оптимальные распределения, для которой выполняется
(12)
Функции
распределения
называют оптимальными
смешанными стратегиями
соответственно для первого и второго игроков-стратегов.
К такого
рода решениям приводят многие малоизученные прикладные задачи в
смешанных стратегиях. Рассмотрим в качестве примера задачу об
одновременном преследовании друг друга на плоскости. Игра
заключается в преследовании друг друга при условии, что игрок
выбирает в качестве своей стратегии некоторую точку
игрок
-
точку
При совершении выбора игроки не имеют информации о выборе противной
стороны. Цель одного из игроков заключается в минимизации расстояния
между ними. Его функция выигрыша определяется как расстояние между
точками
Обычно в качестве областей
рассматриваются круги, их части или кольца различных радиусов. Это
достаточно сложные задачи, мало изученные в общих и частных
постановках.
Литература:
Петросян Л.А., Зенкевич Н.А., Семина Е.А.Теория игр. – М.: Высш.шк., Книжный дом «Университет», 1998. – 304 с.
Кинси Д.М. – Введение в теорию игр. – М., Физ.-мат.лит., 1960.- 420 с.
Айзекс Р. Дифференциальные игры. – М.: Мир, 1967. – 480 с.
Вентцель Е.С. Элементы теории игр. М.: Наука, 2008. - 360 с.
Покорная О.Ю. О выборе оптимальных стратегий в планировании боевых операций. Инновации в авиационных комплексах и системах военного назначения. Воронеж, ВАИУ, Ч.10, 2009, с.194-198.
