Разработка заданий суммативного оценивания за раздел по математике для 6-х классов

В этой статье рассматривается структура разработки заданий суммативного оценивания за раздел для учащихся 6-х классов общеобразовательных школ для разных образовательных групп учащихся. Показана важность дифференцированного подхода при использовании заданий суммативного оценивания для учащихся 6-х классов.

Ключевые слова: структура, суммативное оценивание, критерий, анализ, результат.

Введение

Значение оценивания в развитии образовательной системы уникально, так как именно оценивание является наиболее очевидным показателем уровня школьного образования, основным индикатором диагностики проблем обучения и средством осуществления обратной связи. Под системой оценивания при этом понимается не только шкала отметок и моменты, в которые отметки выставляют учащимся, но в целом механизм контрольно-диагностической связи между учеником, учителем и родителями.

Суммативное оценивание за раздел в школьном образовании, нацелено на мониторинг индивидуального прогресса и мотивирование учащихся на выстраивание индивидуальной траектории развития. Использование системы суммативного оценивания заключается в сравнении достижений школьника с определенными, коллективно выработанными, заранее известными всем субъектам образовательного процесса критериями. При этом оцениваемая работа позволяет самому ученику рефлексировать свои успехи и неудачи, не только усваивать знания, но и применять их, многопланово анализировать собственные действия, организовывать эффективное взаимодействие с учителем

Активность учащегося, его включенность в учебный процесс обеспечивается тем, что критериальное оценивание выполняет функцию обратной связи, когда ученик получает информацию о своих успехах и неудачах. Тем самым решая проблему объективного оценивания учащихся, суммативный подход стимулирует их на достижение не только более высокого результата, но и на самостоятельную постановку целей в учебном процессе.

Основная часть

Суммативное оценивание за раздел — это оценивание учебных достижений по завершении определенного изученного материала, то есть «подсчет» достижений учащихся по итогу темы, раздела [1, c. 23].

Начинать составление заданий для суммативного оценивания следует с обзора учебной программы и плана. Следующим шагом является анализ цели обучения, на основании чего и будут составляться критерии оценивания. Если критерии оценивания соответствуют проверяемым целям, то следующий шаг — составление заданий. При составлении заданий для суммативного оценивания за раздел учитель может использовать или адаптировать образцы, предложенные в методических рекомендациях по суммативному оцениванию. Кроме этого, учителю предлагается самостоятельно разработать инструменты оценивания согласно установленному алгоритму.

На практике столкнулись с тем, что задания в методических рекомендациях нацелены на среднего ученика. А как бы с детьми, которые являются учащимися общеобразовательной школы, но с особыми образовательными потребностями? Рекомендованные задания для таких учеников сложные, требуют больше времени для выполнения, а также отрицательно влияют на эмоциональное состояние ученика [2, с. 23–24, с. 27–28].

1. При каком значении b уравнения будут равносильными:

2х — 9 = 3 и х + 3b = — 10 ?

2. Решите уравнение:

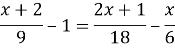
3. Решите уравнение: 5| х — 4| = 135.

4. В одном шкафу было в 4 раза меньше книг, чем в другом. Когда в первый шкаф положили 17 книг, а из второго взяли 25, то в обоих шкафах книг стало поровну. Сколько книг было в каждом шкафу [3, c. 16–17]?

Данные задания вызвали затруднения у низко мотивированных учащихся, а также учащихся с особыми образовательными потребностями. Это было выявлено при проведении анализа суммативной работы за раздел. Наглядно можно увидеть в таблице 1.

Цель: определить уровень достижения целей обучения за раздел

1. Анализ Сор показал следующий уровень учебных достижений (УУД) учащихся:

Таблица 1

Для раздела «Линейные неравенства с одной переменной» задания для суммативного оценивания были разработаны самостоятельно, учитывая вышеизложенные требования. Анализ суммативного оценивания показал следующий результат в таблице 2:

Цель: определить уровень достижения целей обучения за раздел

1. Анализ Сор показал следующий уровень учебных достижений (УУД) учащихся:

Таблица 2

Анализ суммативного оценивания

Заключение.

Анализ показал, что при использовании заданий суммативного оценивая из сборника учащиеся показали результат хуже, чем при использовании заданий, составленных дифференцируемо: отдельно для учащихся основного класса и для учащихся с особыми образовательными потребности. Наглядно это можно заметить на рис. 1.

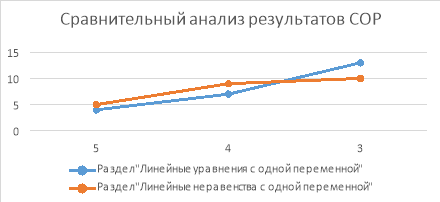
Рис. 1

Следовательно, можно сделать вывод о том, что при проведении суммативного оценивания за раздел нужно подбирать такие задания, чтобы были понятны и ясны не только среднему и сильному ученику класса, но и для слабо мотивированных учащихся, и для учащихся с особыми образовательными потребностями.

1. Автономная организация образования «Назарбаев интеллектуальные школы» Руководство по критериальному оцениванию для учителей основной и общей средней школ Учебно-методическое пособие Астана, 2017
2. Руководство по критериальному оцениванию для учителей основной и общей средней школы, учебно-методическое пособие, Астана, 2017 г,
3. Модель критериального оценивания. Утверждены решением Правления АОО «Назарбаев Интеллектуальные школы» от 15 августа 2016 года (протокол № 39) (с изменениями и дополнением от 17.08.2017 № 42, 22.08.2018 № 48; 21.06.2019 № 23; 15.08.2019 № 37)