Известно, что график движения поездов выражает принятый для данного участка или железнодорожной линии способ организации перевозок на железных дорогах. График движения объединяет в единое целое работу станций, локомотивных депо, тяговых подстанций, пункта осмотра и ремонта вагонов, дистанций пути, дистанции сигнализации и связи и других подразделений железных дорог, связанных с движением поездов, обеспечивая их согласованную работу.
От качественного составления графика движения зависит:
– удовлетворение потребностей в перевозках пассажиров и грузов;
– безопасность движения поездов;
– наиболее эффективное использование пропускной и провозной способности участков и перерабатывающей способности станций;
– рациональное использование подвижного состава;
– соблюдение установленной продолжительности непрерывной работы локомотивных бригад;
– возможность производства работ по текущему содержанию и ремонту пути, сооружений, устройств СЦБ, связи и электроснабжения.
В данной работе мы рассмотрим подход к графику движения, основанный на методах современной топологии малых размерностей. Также мы рассмотрим ряд задач, которые возможно решить этими методами, повысив при этом пропускную способность графика, давая возможность для прокладки новых ниток поездов. Топологический аппарат, предлагаемый в работе, является новым. Часть его была разработана в первой половине XX века выдающимися топологами, такими как Эмиль Артин, Курт Рейдемейстер, Джеймс Александер и др. Далее в течение нескольких десятилетий в данной топологической области был «застой», и лишь в конце 1980-х годов произошел серьезный скачок в развитии, благодаря новозеландскому математику Вогану Джонсу, который предложил более тонкий подход к вычислению полиномиальных инвариантов, названных позднее в его честь.
Особенностью описываемого нами подхода является тот факт, что визуально-геометрическая структура графика движения переводится на алгебраический язык, позволяя использовать аппарат непрерывных преобразований, изменяя саму структуру графика в зависимости от постановки задачи, а также — добавляя новые нитки поездов.
Интервалом неодновременного прибытия поезда с остановкой и проследовании без остановки встречного поезда ![]() является минимальное время от момента прибытия на раздельный пункт грузового или пассажирского поезда с остановкой до момента проследования без остановки встречного грузового (рис. 1, а) или пассажирского (рис. 1, б).
является минимальное время от момента прибытия на раздельный пункт грузового или пассажирского поезда с остановкой до момента проследования без остановки встречного грузового (рис. 1, а) или пассажирского (рис. 1, б).
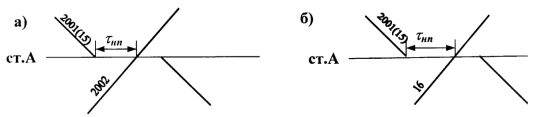
Рис. 1. Интервалы неодновременного прибытия поезда с остановкой и проследования без остановки встречного поезда: а) грузового (или пассажирского) и грузового; б) грузового (или пассажирского) и пассажирског
Интервалом скрещения поездов ![]() является минимальное время от момента прибытия (рис. 2, а) либо проследования (рис. 2,б) раздельного пункта грузовым или пассажирским поездом до момента отправления на тот же перегон встречного грузового или пассажирского поезда.
является минимальное время от момента прибытия (рис. 2, а) либо проследования (рис. 2,б) раздельного пункта грузовым или пассажирским поездом до момента отправления на тот же перегон встречного грузового или пассажирского поезда.

Рис. 2. Интервалы скрещения грузовых (пассажирских) поездов: а) при остановке прибывающего поезда; б) при проследовании прибывающего поезда без остановки
На первом этапе решения задачи представленные интервалы моделируются в виде соотношений в математической косе. В интуитивном представлении под косой понимается множество нитей, запутанных некоторым определенным образом. Более точно можно представить косу из ![]() нитей как
нитей как ![]() тонких бечевок, подвешенных «вверху» (на гвозди, выстроенные в горизонтальную линию) и переплетающихся друг с другом в своем движении «вниз» (движение вверх не допускается); по прибытии вниз мы находим те же нити (также зафиксированные гвоздями), но не обязательно в том же порядке. Пример такого моделирования графика движения поездов в виде математической косы представлен на рис. 3.
тонких бечевок, подвешенных «вверху» (на гвозди, выстроенные в горизонтальную линию) и переплетающихся друг с другом в своем движении «вниз» (движение вверх не допускается); по прибытии вниз мы находим те же нити (также зафиксированные гвоздями), но не обязательно в том же порядке. Пример такого моделирования графика движения поездов в виде математической косы представлен на рис. 3.
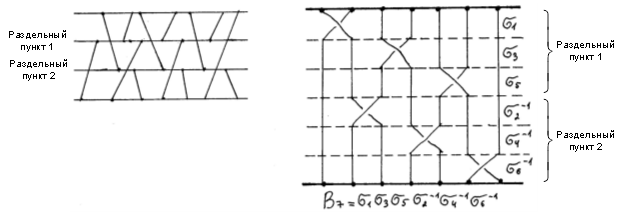
Рис. 3. Представление графика движения поездов с семью нитками в виде математической косы ![]()
Элементы пересечения нитей в косе ![]() называются соотношениями и обозначаются
называются соотношениями и обозначаются ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
На множестве кос ![]() выполняется операция произведения (при условии, что количество нитей сохраняется). Эта операция заключается в последовательном связывании кос (соединении верхних концов нитей второй косы с нижними концами нитей первой).
выполняется операция произведения (при условии, что количество нитей сохраняется). Эта операция заключается в последовательном связывании кос (соединении верхних концов нитей второй косы с нижними концами нитей первой).
Важно отметить, что произведение кос обладает многими свойствами обычного произведения чисел. Прежде всего, имеется единичная коса (обозначается ![]() ), т. е. коса, которая, как и число 1, не изменяет то, что на нее умножается. Это тривиальная коса, нити которой спадают вертикально, не переплетаясь. Действительно, прикрепление снизу тривиальной косы к данной косе приводит лишь к удлинению ее нитей и не изменяет тип косы.
), т. е. коса, которая, как и число 1, не изменяет то, что на нее умножается. Это тривиальная коса, нити которой спадают вертикально, не переплетаясь. Действительно, прикрепление снизу тривиальной косы к данной косе приводит лишь к удлинению ее нитей и не изменяет тип косы.
Во-вторых, для каждой косы ![]() существует коса, называемая обратной, и обозначается
существует коса, называемая обратной, и обозначается ![]() , такая, что ее произведение с
, такая, что ее произведение с ![]() дает тривиальную косу:
дает тривиальную косу: ![]() . Эта коса получается, если взять отражение косы в горизонтальном зеркале; действительно, каждый перекресток уничтожается своим зеркальным изображением, таким образом, все перекрестки взаимно уничтожаются попарно шаг за шагом, начиная с середины косы-произведения.
. Эта коса получается, если взять отражение косы в горизонтальном зеркале; действительно, каждый перекресток уничтожается своим зеркальным изображением, таким образом, все перекрестки взаимно уничтожаются попарно шаг за шагом, начиная с середины косы-произведения.
Третье свойство, которым обладают косы — это ассоциативность произведения.
Все вышеперечисленные свойства свидетельствуют о том, что множество кос с ![]() нитями образуют группу.
нитями образуют группу.
Существование произведения кос позволяет заменять рисунок косы, изображающий график движения поездов, некоторым словом — алгебраическим представлением этой косы. Действительно, двигаясь сверху вниз вдоль косы, мы видим, что наша коса — последовательное произведение кос с одним перекрестком в каждой (см. рис. 3); они называются элементарными косами и обозначаются (в случае с ![]() нитями)
нитями) ![]() ,
, ![]() ,...,
,..., ![]() .
.
Таким образом, мы заменим косы — геометрические объекты — словами, их алгебраическими кодами.
Между косами существует отношение эквивалентности (изотопия). Применительно к графику движения поездов мы расширили классические соотношения Э. Артина, полученные им для писания изотопии. Эти расширенные соотношения имеют вид:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() .
.
Сравнение различных вариантов графика движения поездов осуществляется посредством теоремы Артина, которая утверждает, что две косы изотопны тогда и только тогда, когда слово, представляющее одну из них, может быть преобразовано в слово, представляющее другую, с помощью последовательности допустимых преобразований.

Рис. 4. Эмиль Артин (1898–1962)
Важность этой теоремы объясняется тем, что она сводит наглядное и визуальное изучение графика движения поездов к их алгебраическому изучению, заведомо более эффективному (а также доступному для компьютеров). Именно этот алгебраический подход к графику движения позволяет нам их классифицировать, т. е. описывать алгоритм сравнения, который для каждой пары кос говорит нам «нет», если они не изотопны, и «да», если они изотопны (в последнем случае он дает к тому же последовательность допустимых преобразований, переводящую одну косу в другую).
На втором этапе решения задачи математическая коса превращается в узел с помощью операции замыкания, которая представляет собой соединение верхних концов нитей с нижними. Данная операция выполняется при условии замыкания, которое не образует новых двойных точек самопересечения.
Доказанная Дж. Александером в 1923 году теорема говорит о том, что используя операцию замыкания можно получить абсолютно любой узел.
Приведем теперь способ представления любого графика движения поездов в виде планарного графа. Напомним, что граф состоит из набора точек, называемых вершинами, и набора ребер, которые их соединяют. Здесь нас будут интересовать плоские графы, то есть графы, которые лежат на плоскости. Из схемы узла мы создаем соответствующий ей планарный граф следующим образом. Сначала заштрихуем каждую внутреннюю область проекции, чтобы внешняя область не была затенена (рис. 5).

Рис. 5. Проекции затененной области
Поместим вершину в центр каждой затененной области и затем соединим с ребром любые две вершины, находящиеся в областях, которые разделяют пересечения (рис. 6). Мы получим график, соответствующий нашей проекции. Существует всего лишь одна проблема ‒ как на получившемся графе отразятся точки пересечения в узле? Эта проблемы решается путем присвоения пересечениям положительного или отрицательного значения, в зависимости от того, как они пересекаются (рис. 7). Мы помечаем каждое ребро на плоском графе знаком + или -, в зависимости от того, проходит ли ребро через + или -. Получившийся граф мы называем помеченным плоским графом (рис. 8). Теперь у нас есть способ превратить любую проекцию узла в помеченный граф.
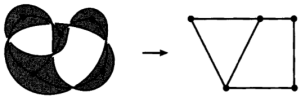
Рис. 6. Граф из проекции узла

Рис. 7. Знаки на перекрестках
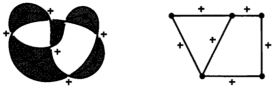
Рис. 8. Планарный граф со знаками из проекции узла
Но что делать если условия задачи будут от нас требовать пойти обратным путем? Можем ли мы превратить любой помеченный планарный граф в проекцию узла? Да, Конечно. Начнем с того, что в помеченном плоском графе поставим крестик на каждом ребре, как показано на рис. 9, b. Соединим ребра внутри каждой области графа, как показано на рис. 9, c. Заштрихуем те области, которые содержат вершину. Затем, в каждом из крестиков поместим пересечение, соответствующее тому, является ли ребро ребром + или -. Результатом является узел (рис. 10).
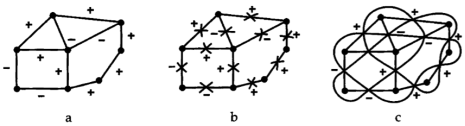
Рис. 9. Превращение помеченного планарного графа в узел
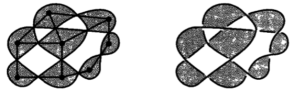
Рис. 10. Узел, созданный из помеченного планарного графа
Покажем теперь как на планарном графе, представляющем график движения поездов, определяется его структура. Иными словами, мы приведем способ расчета, который позволит понять, будут ли существовать в моделируемом графе циклы, то есть замкнутые пути, в которых совпадают начальная и конечная вершины. В действительности, мы поговорим об одном из самых удачных и интересных способов различать узлы. Каждому узлу мы сопоставляем полином. Мы вычислим многочлен из проекции узла, но любые две разные проекции одного и того же узла дают один и тот же многочлен. Таким образом, многочлен является инвариантом узла. Если у нас есть проекции двух узлов, а вычисленные многочлены различны, это немедленно говорит нам о том, что эти два узла должны различаться.
Прежде чем мы введем любой из многочленов, взглянем на историю полиномиальных инвариантов узлов и зацеплений. Первый полином, связанный с узлами и зацеплениями, был создан Дж. Александером примерно в 1928 году. Этот полиномиальный инвариант был очень хорош при различении узлов и зацеплений. Математики использовали многочлен Александера, чтобы различать узлы и зацепления в течение следующих 58 лет. В 1969 году Джон Конвей нашел способ вычислить многочлен Александера для узлов, используя так называемое скейн-соотношение. Это уравнение, которое связывает полином узла с полиномом узла, полученным путем изменения пересечений в проекции исходного узла.
В 1984 году Воган Джонс, математик из Новой Зеландии, открыл новый многочлен для узлов и зацеплений. Полином вышел из работы, которую он выполнял над алгебрами операторов, областью математики, ранее не связанной с теорией узлов. Он случайно заметил, что отношения, возникающие в операторных алгебрах, очень похожи на отношения, возникающие в теории узлов. Это привело его к открытию нового многочлена для узлов.
Открытие Джонса вызвало огромное волнение среди теоретиков узлов. Многие из них стали работать над полиномами. Через четыре месяца после того, как Джонс сообщил о своем новом полиноме, было объявлено об открытии полинома HOMFLY. Название HOMFLY происходит от первых букв имен первооткрывателей Хоста, Окнеану, Миллета, Фрейда, Ликориша и Йеттера. Удивительно, но этот же многочлен был обнаружен этими людьми, когда они работали в четырех разных независимых группах. Пара польских математиков по имени Przytycki и Traczyk также разработала один и тот же многочлен независимо, но их работа пришла по почте только через несколько месяцев. С тех пор было обнаружено множество других многочленов, различающих узлы и зацепления.
Мы начнем с обсуждения полинома Джонса, как его понимает Луи Кауфман, математик из Университета Иллинойса в Чикаго. Чтобы определить многочлен Джонса, мы сначала разработаем многочлен, связанный с узлами, который называется скобочным многочленом. При разработке полинома-скобки мы используем подход, который математик использовал бы, если бы он или она пытался обнаружить полином, инвариантный для узлов и зацеплений.
Давайте предположим, что мы пытаемся создать этот полиномиальный инвариант для узлов и зацеплений, и что у нас есть несколько требований к нему. Прежде всего, мы хотели бы, чтобы полином тривиального узла был равен 1. Если мы используем обозначение ![]() для скобочного полинома узла
для скобочного полинома узла ![]() , то наше первое правило становится следующим:
, то наше первое правило становится следующим:
![]()
Во-вторых, мы хотим получить скобочный полином узла в терминах скобочных полиномов простых узлов. Учитывая пересечение в нашей проекции узла, мы разделяем ее по вертикали и горизонтали, чтобы получить две новые проекции узла, каждая из которых имеет на одно пересечение меньше. Мы делаем скобочный многочлен нашей проекции узла линейной комбинацией скобочных многочленов двух наших новых проекций узла, где мы еще не определились с коэффициентами, поэтому мы просто называем их ![]() и
и ![]() .
.
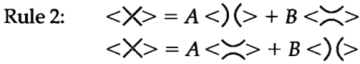
Второе уравнение здесь является только первым уравнением, но рассматривается с перпендикулярной точки зрения. Применение первого уравнения в правиле 2 дает нам точно второе уравнение, поэтому мы не рассматриваем эти два уравнения как отдельные. Наконец, нам нужно правило для добавления в узел тривиального компонента (результатом которого всегда будет разделенный узел). Итак, мы скажем:
![]()
Каждый раз, когда мы добавляем дополнительный тривиальный компонент, который не связан с исходным узлом ![]() , мы просто умножаем весь полином на
, мы просто умножаем весь полином на ![]() . Как и в случае с
. Как и в случае с ![]() и
и ![]() , мы рассматриваем
, мы рассматриваем ![]() как переменную в полиноме на данный момент.
как переменную в полиноме на данный момент.
Наиболее важным критерием для нашего полинома является то, что он представляет собой инвариант для узлов. То есть вычисление многочлена не может зависеть от конкретной проекции, с которой мы начали. Сама проекция должна быть эквивалентна всем другим проекциям, получившимся из нее, но различающимся движениями Рейдемейстера. Начнем с движения Рейдемейстера II типа. Мы хотим, чтобы
![]()
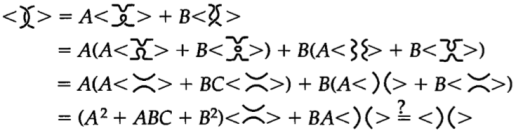
Чтобы этот многочлен не изменился при этом движении, мы вынуждены сделать ![]() , чтобы коэффициент ровнялся единице. Но это вполне нормально. В любом случае, мы не стремились к тому, чтобы в последнем полиноме была буква
, чтобы коэффициент ровнялся единице. Но это вполне нормально. В любом случае, мы не стремились к тому, чтобы в последнем полиноме была буква ![]() . После того, как мы заменили
. После того, как мы заменили ![]() на
на ![]() , очевидно, что нам также нужно
, очевидно, что нам также нужно ![]() , так что коэффициент перед горизонтальным разделением нитей узла равен нулю. Это означает, что мы должны сделать
, так что коэффициент перед горизонтальным разделением нитей узла равен нулю. Это означает, что мы должны сделать ![]() . Тогда полином скобки будет неизменным при движении Рейдемейстера II типа. Следовательно, с этого момента наши три правила вычисления полинома скобок становятся:
. Тогда полином скобки будет неизменным при движении Рейдемейстера II типа. Следовательно, с этого момента наши три правила вычисления полинома скобок становятся:
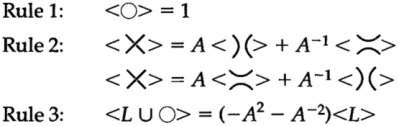
Обратите внимание, что наш полином теперь имеет единственную оставшуюся переменную ![]() .
.
Теперь давайте посмотрим, как третье движение Рейдемейстера влияет на полином (рис. 2). Движение III типа также на него не влияет.
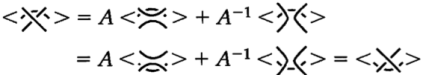
Прежде чем мы обсудим движение Рейдемейстера I типа, давайте сделаем пару быстрых вычислений с нашим полиномом. Сначала мы просто используем правила 1 и 3 для вычисления полинома обычной проекции тривиального зацепления, состоящего из двух компонентов. По правилу 3, где мы позволяем ![]() быть узлом, мы имеем
быть узлом, мы имеем
![]()
Давайте попробуем вычислить скобочный многочлен проекции простейшего нетривиального зацепления, состоящего из двух компонентов (зацепление Хопфа), представляющее косу графика движения поездов с кодировкой ![]() . На этот раз мы будем использовать все три правила.
. На этот раз мы будем использовать все три правила.
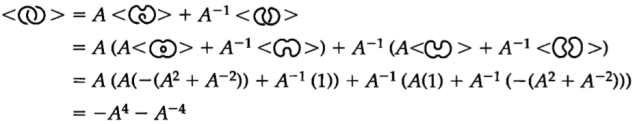
Полученная скобка Кауфмана свидетельствует о том, что данное зацепление является нетривиальным. Это означает, что граф, моделирующий график движения, содержит циклы.
В качестве упражнения мы предлагаем читателю самому определить скобку Кауфмана для узла «трилистника» и убедиться, что этот граф также будет иметь циклы.
Давайте теперь посмотрим, что происходит с полиномом, когда мы применяем движение Рейдемейстера I типа.
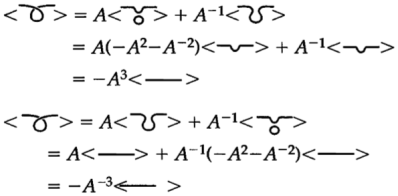
Как видно из вычисления, скобочный полином был изменен при первом движении Рейдемейстера. Это означает, что он зависит от того, какая проекция узла у нас есть.
Подводя итог вышеизложенному можно сказать:
- Графовое представление графика движения поездов очень удобно для понимания его структуры, которая в дальнейшем может быть изучена с помощью топологических индексов. Эти индексы представляют собой числовые значения, отображающие степень разветвленности графов. Кроме того, с помощью этих индексов возможно обнаружить топологически эквивалентные графы.
- Так как тривиальные узлы влекут за собой отсутствие циклов на графах, этот факт возможно обнаружить рассчитав полином Джонса для этих узлов, который должен равняться единице. Это утверждение верно и в обратном: нетривиальные узлы с полиномом Джонса, отличным от единицы, свидетельствуют о наличии в графах циклов.
Особый интерес в косах представляют комбинаторные алгоритмы, позволяющие определить структуру графика движения поездов с минимальным временным интервалом между моментом отправления первого поезда и моментом прибытия последнего поезда на раздельный пункт. В дальнейшем мы рассмотрим такие алгоритмы.
В списке литературы приводится перечень источников по топологическим вопросам. Для начального ознакомления с топологией интересны книги [1, 4, 6]. Для более детального и глубокого ознакомления — книги [2, 3, 5]
Один из авторов этой статьи считает своим долгом сердечно поблагодарить известного тополога и популяризатора математики, сотрудника Независимого московского университета Алексея Брониславовича Сосинского за приятное и плодотворное сотрудничество.
Литература:
- Болтянский В. Г. Наглядная топология / В. Г. Болтянский, В. А. Ефремович — М.: Книга по требованию, 2012. — 160 с.
- Дужин С. В., Чмутов С. В. Узлы и их инварианты // Математическое просвещение. — 1999. — № 3. — С. 59–93
- Мантуров В. О. Лекции по теории узлов и их инвариантов. — М.: Эдиториал УРСС, 2001. — 304 с.
- Прасолов В. В. Наглядная топология. — 4-е изд., стереотип. — М.: МЦНМО, 2015. — 112 с.: ил.
- Прасолов В. В., Сосинский А. Б. Узлы, зацепления, косы и трехмерные многообразия. — М.: Изд-во МЦНМО, 1997. — 352 с.
- Сосинский А. Б. Узлы и косы. — 2-е изд., стереотип. — М.: Изд-во МЦНМО, 2012. — 24 с

