Задачами линейного программирования называются задачи, в которых требуется найти наибольшее или наименьшее значение (или экстремум) некоторой линейной функции при наличии некоторых ограничений на переменные, причём все ограничения заданы в виде линейных равенств или неравенств.
Модель задачи линейного программирования имеет вид:
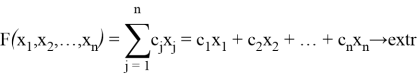
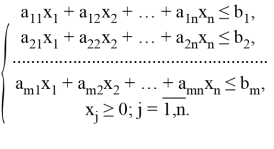
Функция 
называется целевой функцией, набор переменных 
, удовлетворяющий системе ограничений, называется допустимым решением (или планом). Множество всех допустимых решений называется областью допустимых решений (ОДР). Допустимое решение, при котором достигается экстремум целевой функции, называется оптимальным решением (оптимальным планом).
Применительно к школьному курсу математики можно рассматривать задачи линейного программирования, содержащие две переменные. Модель задачи в этом случае имеет вид:
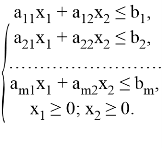
В этом случае задачу можно решить графическим способом. Действительно, целевая функция является линейной, и её линией уровня будет прямая. Все неравенства в системе ограничений являются линейными, решение каждого неравенства можно изобразить на плоскости как полуплоскость, расположенную по одну сторону от некоторой прямой. Таким образом, пересечение всех полуплоскостей и будет являться областью допустимых решений. В школьном курсе математики рассматриваются методы решения системы линейных неравенств, основанные на геометрических построениях. Пересечение плоскостей обычно представляет собой некоторый выпуклый многоугольник, и его построение в прямоугольной системе координат не должно вызывать особых сложностей для учеников. Понятие линии уровня также встречается в школьном курсе, причём не только в математике, но и в физике, географии и других дисциплинах. Изменение линии уровня означает изменение значения целевой функции, и рассматривается направление, в котором происходит увеличение (или уменьшение) значения целевой функции. Это направление связано с понятием нормального вектора к прямой. Таким образом, можно наглядно проиллюстрировать поиск оптимального решения из области допустимых решений, перемещая линию уровня до достижения крайних точек ОДР.
Проиллюстрируем на примере решение задачи с экономическим содержанием. Пусть швейная фабрика выпускает мужские и женские костюмы, и для их пошива использует ткани четырёх видов
Известны величины расходов каждого вида ткани на производство одного мужского и одного женского костюма, а также имеющиеся запасы тканей, заданные в таблице:
|
Виды тканей |
Расход ткани на изготовление одного костюма (условных единиц) |
Запасы тканей (тыс. усл. ед.) |
|
|
Мужские костюмы |
Женские костюмы |
||
|
A |
2 |
4 |
32 |
|
B |
3 |
2 |
24 |
|
C |
3 |
0 |
18 |
|
D |
0 |
4 |
28 |
Известно, что реализация одного мужского костюма приносит доход в 3 условных единиц, а одного женского — 4 условных единиц. Требуется составить оптимальный план выпуска товаров, то есть такой план, при котором с учётом имеющихся ресурсов тканей доход от реализации костюмов будет наибольшим.
Решение
Построим математическую модель задачи. Введём переменные 
— количество мужских и женских костюмов соответственно (тыс. шт.). Тогда суммарный доход от их реализации определяется выражением
,
которое нужно максимизировать. По имеющимся исходным данным определяем ограничения по ресурсам каждого вида тканей. Они определяются неравенствами:
— для тканей вида 
;
— для тканей вида 
;
— для тканей вида 
;
— для тканей вида 
.
Количество выпускаемых костюмов есть величина неотрицательная, поэтому 
Таким образом, получаем:
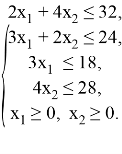
Построим область допустимых решений. Заменив в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств на знаки точных равенств, построим по двум контрольным точкам прямые, соответствующие этим равенствам, и для удобства пронумеруем все прямые:
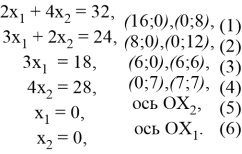
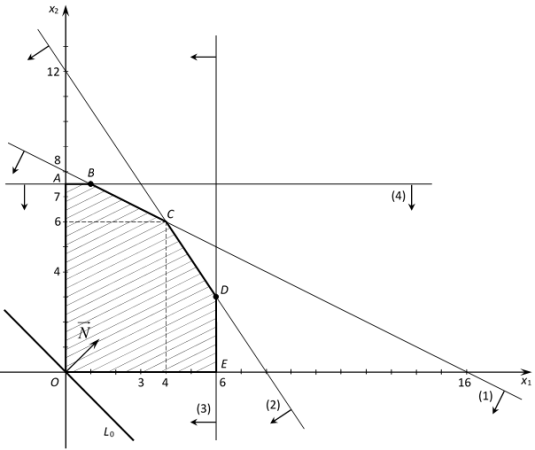
Построим полуплоскости с этими граничными прямыми и найдём их пересечение. Получим шестиугольник 
, который и представляет собой ОДР. Затем строим линию нулевого уровня 
она пройдёт через начало координат, построим также нормальный вектор 
Передвигая линию уровня 
в направлении вектора 
параллельно самой себе, найдём крайнюю точку выхода из ОДР, в которой линия уровня займёт положение опорной прямой. В нашем случае это будет точка , которая будет точкой максимума целевой функции. Найдём координаты точки как точки пересечения прямых 
и 
, решив систему уравнений:
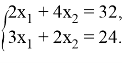
В результате получим:
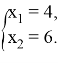
Значит, 
— точка максимума, и тогда
.
Таким образом, фабрике следует выпускать 4 тысячи мужских костюмов и 6 тысяч женских костюмов, при этом доход будет наибольшим и составит 36 тысяч условных единиц.
Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи рационального использования сырья и материалов; оптимизации раскроя; оптимизации производственной программы предприятий; оптимального размещения и концентрации производства; составления оптимального плана перевозок, работы транспорта; управления производственными запасами· и многие другие, принадлежащие сфере оптимального планирования. Линейное программирование применимо для построения математических моделей тех процессов, в основу которых может быть положена гипотеза линейного представления реального мира. Подобных примеров существует огромное множество, и это указывает на актуальность и практическую значимость рассматриваемой темы. В школьном курсе математики задачи линейного программирования можно рассматривать на элективных курсах, кружках и факультативах. Решение этих задач способствует тому, что у учащихся закрепляются междисциплинарные связи между различными дисциплинами. Постановка задач предполагает знание основных экономических понятий и умение моделировать реальные ситуации с привлечением математического аппарата. Решение задач требует познаний в области геометрии и алгебры. Анализ полученных результатов и выводы требуют осмысления содержательной стороны вопроса.
Литература:
- Антонюк, Т. П. Задачи линейного программирования. Т. П. Антонюк // г. Ижевск. Ижевская областная типография, 2008–365с.
- Дорофеев, Г. В. Математика. 5 класс. Часть 1. Л. Г. Петерсон// М.: ООО «БИНОМ. Лаборатория знаний»
- Дорофеев, Г. В. Математика. 5 класс. Часть 2. Л. Г. Петерсон// М.: ООО «БИНОМ. Лаборатория знаний»
- Виленкин, А. Н. Математика 5 класс. Часть 1, А. Н. Виленкин., В. И. Жохов., А. С. Чесноков// М.: Просвещение
- Виленкин, А. Н. Математика 5 класс. Часть 2, А. Н. Виленкин., В. И. Жохов., А. С. Чесноков// М.: Просвещение
- Дорофеев, Г. В. Математика. 5 класс. Г. В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова// Под ред. Г. В. Дорофеева, И. Ф. Шарыгина. — М.: Просвещение
- Дорофеев, Г. В. Математика. 6 класс. Г. В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова// Под ред. Г. В. Дорофеева, И. Ф. Шарыгина. — М.: Просвещение
- Никольская, И. Л. Учимся рассуждать и доказывать. И. Л. Никольская, Е. Е. Семенов // Книга для учащихся 6–10 кл. сред.шк.-М.: Просвещение, 1989. –С. 192.
- Матюшкин, А. М. Проблемные ситуации в мышлении и обучении/ А. М. Матюшкин — М.:«Педагогика», 2007. — 198 с.
- Атанасян, Л. С. Методика преподавания математики в средней школе. / Л. С. Атанасян, — М.: Просвещение, 2012. — 368 с.
