Цель исследования: повышение уровня выполнения заданий, ориентированных на навыки анализа и синтеза у учащихся путем изучения предмета не только со стороны математики, но и с других областей наук.
Задачи:
– Изучить принцип дифференциации «углубление»;
– Провести сравнительный анализ результатов;
– Выявить преимущества и недостатки использования принципа; дифференциации «углубление» на уроках математики.
Актуальность: Использование принципа «углубление» реализуется в процессе преподавания и обучения, как один из инструментов поддержки и развития одаренности у учащихся.
Постановка проблемы исследования: На уроках математики наиболее распространен принцип дифференциации «усложнение», который подразумевает разработку комплексных заданий на основе разноуровневых ресурсов в процессе обучении. Однако, процесс выполнение заданий уровня А, В, С не позволяет учащимся развивать исследовательские навыки и навыки высокого мышления.
Объект исследования — учащиеся 7–8 классов Назарбаев Интеллектуальной школы химико-биологического направления города Актау.
Предмет исследования — урок математики
В целях поддержки одаренности и повышения интереса учащихся к предмету мы решили применить в дальнейшем исследовать передовые методы обучения. Наблюдая за мотивацией учащихся в классе и академической успеваемостью, мы обнаружили, что ученики 7–8 классов были мало заинтересованы на уроках и не проводили анализ собственных действий. Чтобы преодолеть эти проблемы, мы решили использовать несколько методов для определения эффективности дифференцированного подхода с учетом возрастных характеристик, а также развития навыков анализа, синтеза и оценивания.
Мы использовали методы исследования:
- Опрос
- Наблюдение
- Изучение литератур как, руководство учителя Программа «Развитие одаренности детей», статей интернета.
Углубление учебной программы существенно влияет на развитие способностей одаренных учащихся. Этот принцип предполагает более глубокое изучение одаренными учащимися тем, дисциплин или областей знания, что ведет к ряду положительных результатов: высокий уровень компетентности в соответствующей предметной области знания, благоприятные условия для интеллектуального развития учащихся [1, c.109]. Для обеспечения преемственности данного принципа дифференциации был разработан пошаговый алгоритм:
- Изучение среднесрочного плана;
- Выбор подходящего концепта;
- Определение ожидаемого результата;
- Формирование исследовательского вопроса;
- Планирование условий проведения исследований на уроке.
Ожидаемый результат исследования — повышение уровня мотивации и интереса к изучению предмета, а также улучшение качества выполнения заданий, ориентированных на навыки высокого порядка учащихся.
Применяя принцип “углубление” на первоначальных уроках, с целью выполнения работы над одаренностью учащихся, мы акцентировали внимание на группе учеников, отличающихся высоким уровнем усвоения материала. Для того, чтобы рассмотреть теорию предмета математики с разных сторон было решено внедрить в урок элементы интеграции, тем самым мы начинали постепенно внедрять элементы концептуального обучения. На одном из уроков им необходимо было провести анализ исторических фактов, постараться разглядеть неравенства треугольника со стороны исторических событий во время рабовладельческого строя и получится ли у них создать собственную модель обучения, построенную на материалах двух предметов. Суть их работы заключалась в проведении мини-исследований на уроке. Этим заданием учащиеся должны были выйти на задуманный нами концепт: Неравенство (Неравенство треугольника и Неравенство рабовладельческого строя).

Рис. 1. Фрагмент урока
Можно отметить тот факт, что учащиеся отнеслись к таким заданиям очень ответственно и при презентации своей работы смогли удивить остальную группу учеников своими интересными докладами. Такой вид работы не заставил себя долго ждать и уже на последующих уроках было заметно, что у учащихся был явно выражен интерес к обучению предмета. Заметно стала проявляться мотивация к обучению и у учащихся с менее выраженными способностями. Таким образом, планируя и проводя дальнейшие занятия, задания такого рода стали выполнять все учащиеся.
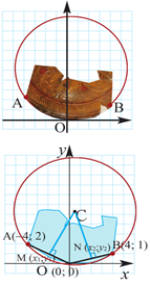
Рис. 2. Фрагмент задания
При изучении темы “Уравнение окружности”, мы решили провести небольшой эксперимент. Учащимся нужно было воссоздать разбитое блюдца из обломков, применяя уравнение окружности.
Так как задание носило прикладной характер, то учащиеся, синтезируя свои знания об окружности, смогли оценить результаты эксперимента благодаря критериям оценивания, составленным совместно с учениками на уроке.
Еще одно задание, которое связано с закреплением изученного раздела “Комбинаторика”, учащиеся восприняли с высоким интересом и увлеченностью. Применяя принцип “углубление”, главной особенностью урока являлось развитие более способных учащихся посредством предоставления им усложненных заданий, при этом не выделяя из общей группы. На этапе вызова первые задания вызывали интерес к обучению, способствовали самостоятельному обобщению знаний по теме. Следующий этап урока был направлен на развитие навыков высокого порядка и критического мышления. Задания были ориентированы на анализ учащимися изученной темы, проблемной ситуацией для них было синтезировать знания, с помощью демонстрации применения комбинаторики в повседневной жизни. Деление на группы производилось по способностям и восприятию учащихся. Так, учащиеся третьей группы выполняли задания общего характера, а первая группа, в составе которой были более способные учащиеся, работали более узко, поскольку их ограничили в конкретной теме, и направлении мини-исследования.
Учащиеся готовили доклад на темы:
1 группа — взаимосвязь комбинаторики и вероятности в науке.
2 группа — применение геометрической вероятности в повседневности.
3 группа — классическая вероятность и я.
Анализируя серию исследуемых уроков, можно выявить как преимущества, так и недостатки принципа “углубление”:
|
Преимущества |
Недостатки |
|
данный принцип позволяет подойти к изучению предмета с различных сторон и способствует более глубокому пониманию в применении на практике; |
занимает большое количество времени как при планировании задания, так и при выполнении его учащимися |
|
способствует развитию навыков критического мышления у учащихся |
мало источников о методе и примерах практики |
|
повышает мотивацию к обучению |
внедрение в предмет, составление прикладных заданий |
|
расширяет кругозор учащихся |
непопулярность данного метода |
|
позволяет составлять урок основываясь на концепт поддержка одаренности учащихся развиваются навыки анализа и синтеза |
Для оценивания проделанной работы, был проведен опрос среди учащихся в устной и электронной форме. Результаты опроса показывают, что большинству понравилась такая форма урока, есть также пару ребят, кто считает данный способ проведения урока бесполезным.
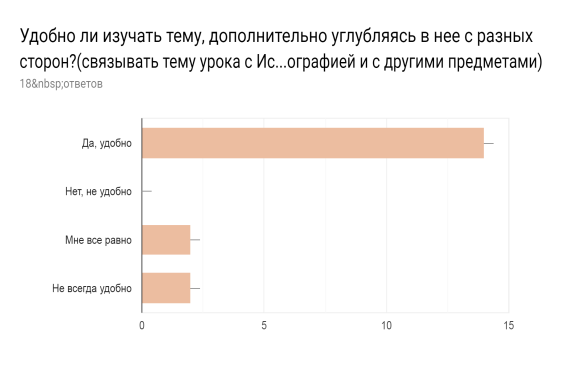
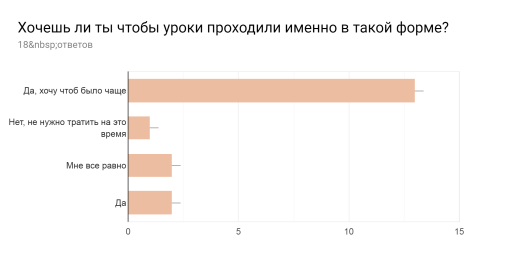
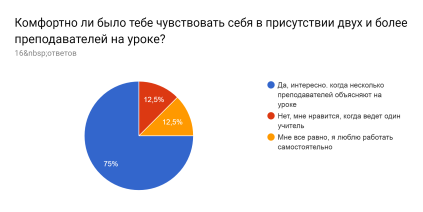
Рис. 3. Результаты опроса
Делая вывод о нашем исследовании, можно сказать, что применение принципа дифференциация, “углубление” в преподавании способствует развитию у учащихся навыков высокого порядка через внедрение концептуального обучения. На данном этапе мы планируем не останавливаться на полученных результатах, а наоборот в дальнейшем будем развиваться в этом направлении поскольку данная методика, еще не развита в наших школах. Метод концептов позволяет создать условия для того, чтобы учащиеся могли проводить связь между предметами и создавать более глубокое понимание и оценивание окружающего мира. Одним из “плодов” данного исследования стало вовлечение учащихся в олимпиадное движение, учащиеся 7–8 классов стали призерами олимпиад на республиканском и международном уровне. Другие учащиеся нашли и реализовали себя в турнире связанным с креативным мышлением, выступали на уровне АО НИШ, заняли второе место на международном турнире “Креатив-бой” (г. Санкт-Петербург, Россия). Учащиеся изменили стиль обучения, что говорит о результативности данного метода на уроках.


Рис. 4.
Литература:
- Программа «Развитие одаренности детей», АОО «Назарбаев Интеллектуальные школы», 2013
- «Психология одаренности: от теории к практике», Москва, Институт психологии РАН, 1999, Авторы: А. Н. Адаскина, Д. В. Ушаков и др.
- Учебно-методическое пособие «Детская одаренность: теория и практика», Блинова В. Л., Блинова Л. Ф., Казань, ТГГПУ, 2010

