Настоящая работа является продолжением статьи «О некоторых непараметрических оценках плотности вероятности и кривой регрессии. Часть 1.», сохраняет все обозначения и посвящена исследованию асимптотических свойств непараметрических оценок плотности распределения вероятности и функции регрессии по экспериментальным данным.
Необходимость исследования новых непараметрических оценок плотности распределения вероятности и кривой регрессии объясняется потребностью в идентификации дискретно-непрерывных процессов, в реальности протекающих при наличии условий А [1]. Эти условия означают, что в выборке «входных - выходных» статистически независимых переменных процесса (x1,y1), (x2y2), … , (xs,ys), где s – количество наблюдений или объем выборки, присутствуют такие особенности, как сгущения, выбросы, разреженности. В таком случае предлагается использовать новые непараметрические оценки плотности распределения вероятности следующего вида:
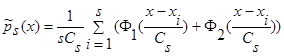 (1)
(1)
и кривой регрессии:
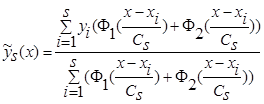 , (2)
, (2)
где знаменатель является оценкой плотности распределения вероятности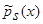 (1) с точностью до
(1) с точностью до 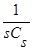 ,
, 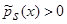 , числитель же обозначим:
, числитель же обозначим:
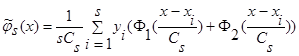 , (3)
, (3)
а интегрируемые с квадратом функции 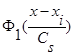 ,
, 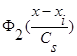 и параметр Cs(коэффициент размытости) таковы, что удовлетворяют условиям сходимости:
и параметр Cs(коэффициент размытости) таковы, что удовлетворяют условиям сходимости:
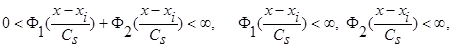
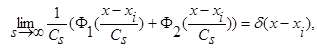
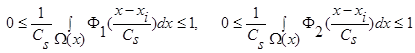
 (4)
(4)
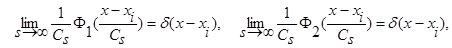
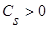 , s=1,2,… ,
, s=1,2,… , 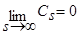 ,
, 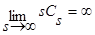 .
.
Функции 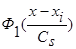 ,
, 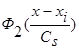 в оценках (1 - 3) четные относительно
в оценках (1 - 3) четные относительно 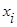 и, например, могут иметь вид, графически представленный на Рис. 1 [1].
и, например, могут иметь вид, графически представленный на Рис. 1 [1].
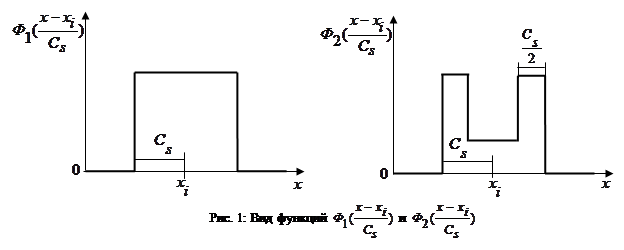
з
Для непараметрической оценки плотности вероятности 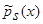 (1) имеет место следующая теорема:
(1) имеет место следующая теорема:
Теорема 1. Пусть р(х) дважды дифференцируема, а функции 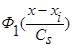 ,
, 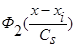 и параметр размытости
и параметр размытости 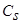 удовлетворяют условиям сходимости (4) и свойству
удовлетворяют условиям сходимости (4) и свойству 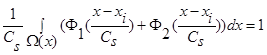 , тогда:
, тогда:
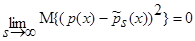 ,
, 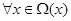 .
.
Доказательству теоремы 1 предпошлем следующую лемму.
Лемма 1.1. Непараметрическая оценка плотности распределения вероятности 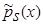 в условиях теоремы 1 является асимптотически несмещенной.
в условиях теоремы 1 является асимптотически несмещенной.
Доказательство леммы 1.1. Возьмем математическое ожидание от 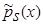 (1):
(1):
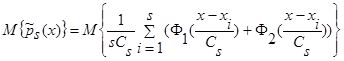 . (5)
. (5)
Воспользуемся свойствами математического ожидания и получим:
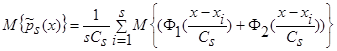 , (6)
, (6)
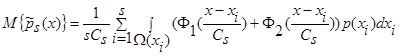 . (7)
. (7)
Поскольку 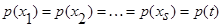 , то имеем s одинаковых интегралов:
, то имеем s одинаковых интегралов:
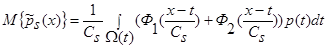 . (8)
. (8)
Сделаем замену переменных:
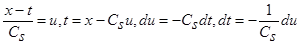 , (9)
, (9)
и, учитывая, что 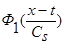 и
и 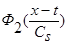 - четные функции относительно
- четные функции относительно 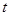 , из выражения (8) получаем:
, из выражения (8) получаем:
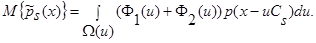 (10)
(10)
Далее разложим 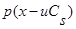 в ряд Тейлора с остаточным членом в форме Лагранжа [2]:
в ряд Тейлора с остаточным членом в форме Лагранжа [2]:
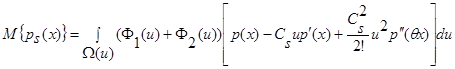 , (11)
, (11)
где 0<θ<1 – некоторая константа.
Воспользуемся свойством интегралов, тогда:
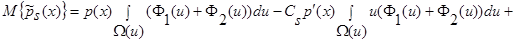
(12)
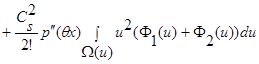 .
.
Применим свойства функций 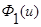 и
и 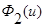 и параметра размытости
и параметра размытости 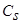 при
при 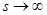 :
: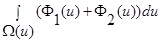 =1, остальные слагаемые обращаются в ноль, поскольку
=1, остальные слагаемые обращаются в ноль, поскольку 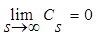 . Следовательно:
. Следовательно:
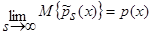 . (13)
. (13)
То есть, оценка функции плотности распределения вероятности 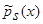 (1) является асимптотически несмещенной.
(1) является асимптотически несмещенной.
Таким образом, лемма 1.1 доказана.
Аналогично выглядит доказательство асимптотической несмещенности оценки плотности распределения вероятности типа оценки 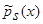 (1), когда вместо суммы двух функций
(1), когда вместо суммы двух функций 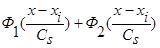 имеем сумму n функций
имеем сумму n функций 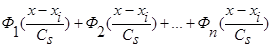 , где n>2 и все n функций удовлетворяют условиям сходимости (4) и свойству
, где n>2 и все n функций удовлетворяют условиям сходимости (4) и свойству 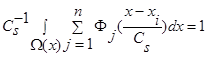 .
.
Доказательство теоремы 1. Возьмем математическое ожидание от 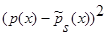 и при
и при 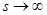 получим:
получим:
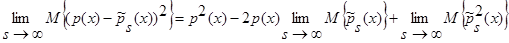 .
.
С учетом леммы 1.1, имеем:
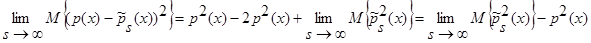 .
.
Докажем, что:
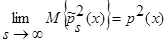 .
.
Вычислим математическое ожидание от квадрата оценки плотности распределения вероятности 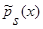 (1):
(1):
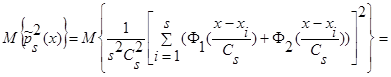
(14)
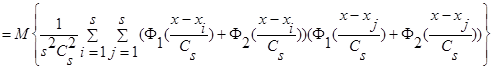 .
.
Двойная сумма разбивается на два слагаемых, первое – когда i=j, второе - когда i≠j, поскольку 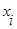 и
и 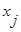 статистически независимы, то есть
статистически независимы, то есть 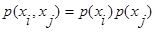 , тогда:
, тогда:
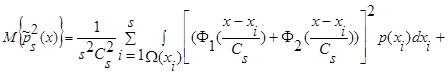
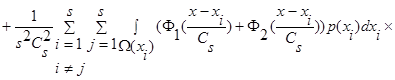 (15)
(15)
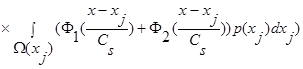 .
.
Поскольку 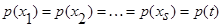 , то:
, то:
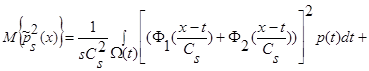
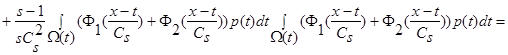 (16)
(16)
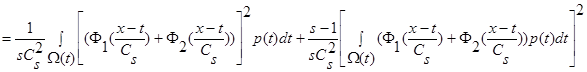 .
.
Сделаем замену переменных (9): 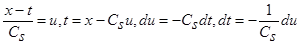 , и, учитывая, что
, и, учитывая, что  и
и 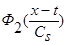 - четные функции относительно
- четные функции относительно 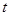 , получаем:
, получаем:
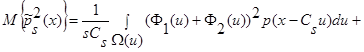
(17)
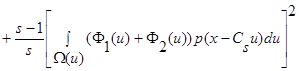 .
.
При 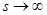 интеграл
интеграл 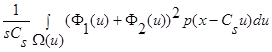 стремится к нулю, поскольку
стремится к нулю, поскольку 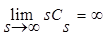 , следовательно:
, следовательно:
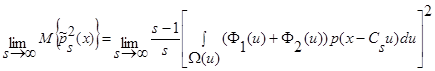 . (18)
. (18)
С учетом условий сходимости и при 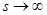
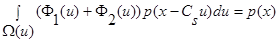 (см. (10) – (13)), то есть:
(см. (10) – (13)), то есть:
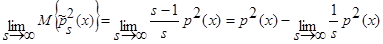 . (19)
. (19)
 Так, как s→∞, то
Так, как s→∞, то 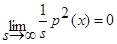 . В итоге получаем:
. В итоге получаем:
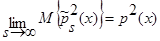 . (20)
. (20)
Тогда 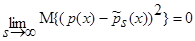 . Таким образом, теорема 1 доказана.
. Таким образом, теорема 1 доказана.
 Аналогично выглядит доказательство теоремы 1, когда в оценке плотности распределения вероятности, типа оценки
Аналогично выглядит доказательство теоремы 1, когда в оценке плотности распределения вероятности, типа оценки 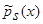 (1), вместо суммы двух функций
(1), вместо суммы двух функций 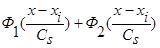 имеем сумму n функций
имеем сумму n функций 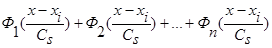 , где n>2 и все n функций удовлетворяют условиям сходимости (4) и свойству
, где n>2 и все n функций удовлетворяют условиям сходимости (4) и свойству 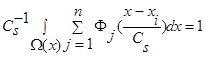 .
.
Для непараметрической оценки кривой регрессии по наблюдениям 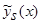 (2) имеет место следующая теорема:
(2) имеет место следующая теорема:
Теорема 2. Пусть у(х) дважды дифференцируема и с вероятностью единица р(х)>0 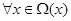 , а функции
, а функции 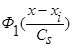 ,
, 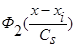 и параметр размытости
и параметр размытости 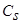 удовлетворяют условиям сходимости (4) и свойству
удовлетворяют условиям сходимости (4) и свойству 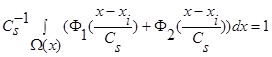 , тогда:
, тогда:
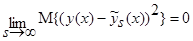 ,
, 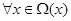 .
.
Произведя простые преобразования, изложенные в [1], можно показать, что [2]:
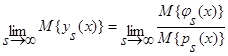 . (21)
. (21)
Доказательству теоремы 2 предпошлем леммы 2.1, 2.2 для оценки 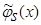 (3) и лемму 2.3 для оценки регрессии
(3) и лемму 2.3 для оценки регрессии 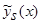 (2).
(2).
Лемма 2.1. Непараметрическая оценка функции 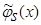 в условиях теоремы 2 является асимптотически несмещенной.
в условиях теоремы 2 является асимптотически несмещенной.
Доказательство леммы 2.1. Вычислим математическое ожидание 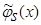 (3):
(3):
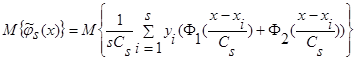 . (22)
. (22)
Произведя в выражении (22) простые преобразования, получим:
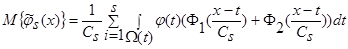 . (23)
. (23)
Сделаем замену переменных (9): 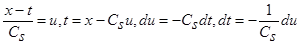 , и, учитывая, что
, и, учитывая, что 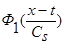 и
и 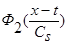 - четные функции относительно
- четные функции относительно 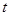 , получаем:
, получаем:
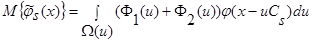 . (24)
. (24)
Далее разложим 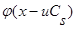 в ряд Тейлора с остаточным членом в форме Лагранжа:
в ряд Тейлора с остаточным членом в форме Лагранжа:
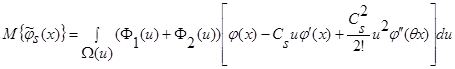 , (25)
, (25)
где 0<θ<1 – некоторая константа.
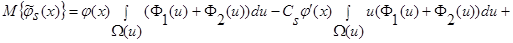
(26)
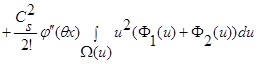 .
.
Применим свойства функций 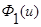 и
и 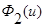 и параметра размытости
и параметра размытости 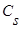 при
при 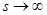 :
: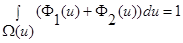 , остальные слагаемые обращаются в ноль, поскольку
, остальные слагаемые обращаются в ноль, поскольку 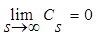 . Следовательно:
. Следовательно:
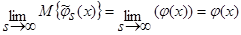 . (27)
. (27)
То есть, оценка 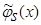 (3) является асимптотически несмещенной.
(3) является асимптотически несмещенной.
Таким образом, лемма 2.1 доказана.
Аналогично выглядит доказательство асимптотической несмещенности оценки функции типа оценки 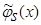 (3), когда вместо суммы двух функций
(3), когда вместо суммы двух функций 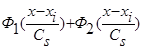 имеем сумму n функций
имеем сумму n функций 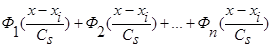 , где n>2 и все n функций удовлетворяют условиям сходимости (4) и свойству
, где n>2 и все n функций удовлетворяют условиям сходимости (4) и свойству 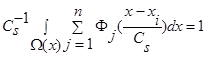 .
.
Лемма 2.2. Пусть φ(х) дважды дифференцируема, а функции 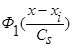 ,
, 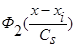 и параметр размытости
и параметр размытости 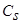 удовлетворяют условиям сходимости (4) и свойству
удовлетворяют условиям сходимости (4) и свойству 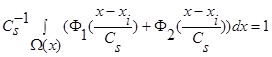 , тогда:
, тогда:
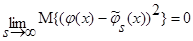 ,
, 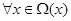 .
.
Доказательство леммы 2.2. Возьмем математическое ожидание от 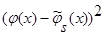 и при
и при 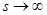 получаем:
получаем:
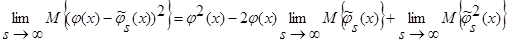 .
.
С учетом леммы 2.1 имеем:
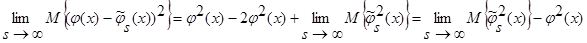 .
.
Докажем, что:
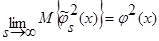 .
.
Вычислим математическое ожидание от квадрата оценки  (3):
(3):
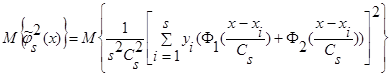 . (28)
. (28)
Произведя в выражении (28) простые преобразования и учитывая, что 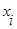 и
и 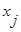 статистически независимы, то есть
статистически независимы, то есть 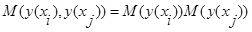 , получим:
, получим:
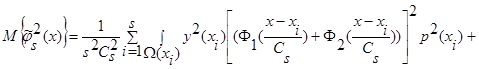
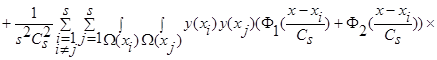 (29)
(29)
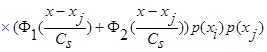 .
.
В силу обозначений 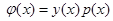 и поскольку
и поскольку 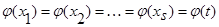 , то:
, то:
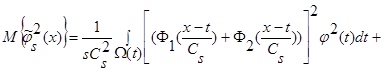
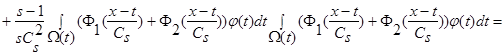 (30)
(30)
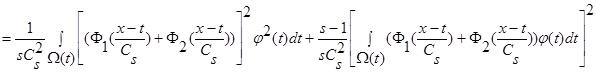 .
.
Сделаем замену переменных (9): 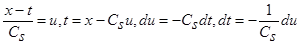 , и, учитывая, что
, и, учитывая, что 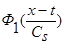 и
и 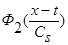 - четные функции относительно
- четные функции относительно 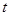 , получаем:
, получаем:
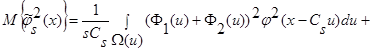
(31)
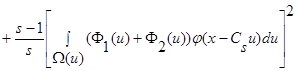 .
.
При 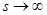 интеграл
интеграл 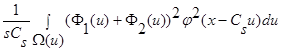 стремится к нулю, поскольку
стремится к нулю, поскольку 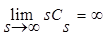 , следовательно:
, следовательно:
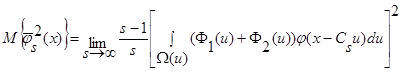 . (32)
. (32)
С учет условий сходимости и при 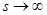
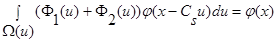 (см. (22) – (27)), тогда:
(см. (22) – (27)), тогда:
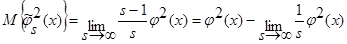 . (33)
. (33)
Так, как s→∞,то 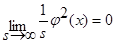 . В итоге имеем:
. В итоге имеем:
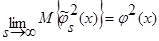 . (34)
. (34)
Таким образом, лемма 2.2 доказана.
Аналогично выглядит доказательство леммы 2.2 для оценки функции типа оценки 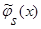 (3), когда вместо суммы двух функций
(3), когда вместо суммы двух функций 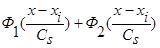 имеем сумму n функций
имеем сумму n функций 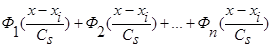 , где n>2 и все n функций удовлетворяют условиям сходимости (4) и свойству
, где n>2 и все n функций удовлетворяют условиям сходимости (4) и свойству 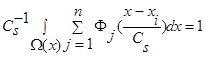 .
.
Лемма 2.3. Непараметрическая оценка регрессии 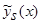 в условиях теоремы 2 является асимптотически несмещенной.
в условиях теоремы 2 является асимптотически несмещенной.
Доказательство леммы 2.3. Возьмем математическое ожидание от оценки регрессии 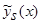 (5):
(5):
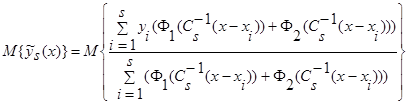 .
.
С учетом (21) при 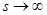 , получим:
, получим:
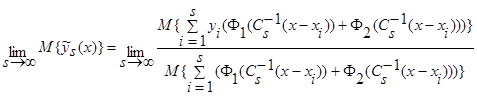 . (35)
. (35)
Поскольку числитель выражения (35) представляет собой математическое ожидание от оценки 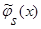 (3), с учетом леммы 2.1
(3), с учетом леммы 2.1 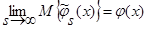 (см. (22) – (27)), а знаменатель – математическое ожидание от оценки плотности распределения вероятности
(см. (22) – (27)), а знаменатель – математическое ожидание от оценки плотности распределения вероятности 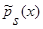 (1), с учетом леммы 1.1
(1), с учетом леммы 1.1 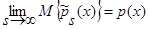 (см. (5) – (13)), тогда:
(см. (5) – (13)), тогда:
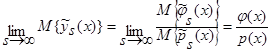 .
.
В силу обозначений 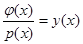 , т.е. оценка регрессии
, т.е. оценка регрессии 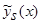 (2) является асимптотически несмещенной:
(2) является асимптотически несмещенной:
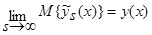 . (36)
. (36)
Таким образом, лемма 2.3 доказана.
Аналогично выглядит доказательство леммы 2.3 для оценки функции регрессии типа оценки 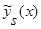 (2), когда вместо суммы двух функций
(2), когда вместо суммы двух функций 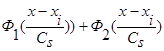 имеем сумму n функций
имеем сумму n функций 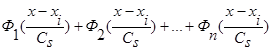 , где n>2 и все n функций удовлетворяют условиям сходимости (4) и свойству
, где n>2 и все n функций удовлетворяют условиям сходимости (4) и свойству 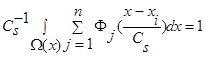 .
.
Доказательство теоремы 2. Возьмем математическое ожидание от 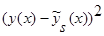 и при
и при 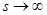 получим:
получим:
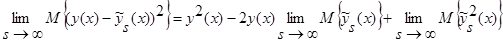 .
.
С учетом леммы 2.3 имеем:
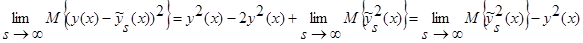 .
.
Докажем, что:
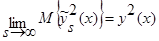 . (37)
. (37)
Возьмем математическое ожидание от квадрата оценки регрессии 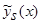 (2):
(2):
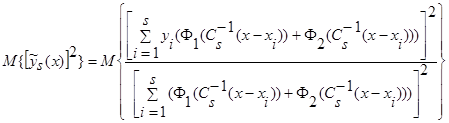 .
.
С учетом (22) при 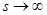 , получим:
, получим:
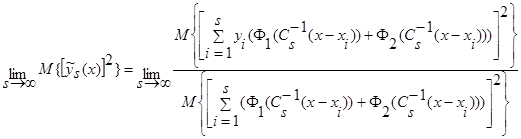 . (38)
. (38)
Поскольку числитель выражения (39) представляет собой математическое ожидание от квадрата оценки 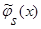 (3), с учетом леммы 2.2
(3), с учетом леммы 2.2 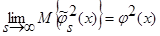 (см. (28) – (34)), а знаменатель – математическое ожидание от квадрата оценки плотности распределения вероятности
(см. (28) – (34)), а знаменатель – математическое ожидание от квадрата оценки плотности распределения вероятности 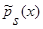 (1), с учетом теоремы 1
(1), с учетом теоремы 1 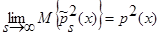 (см. (14) – (20)), тогда:
(см. (14) – (20)), тогда:
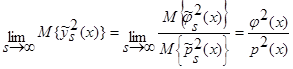 .
.
В силу обозначений 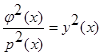 , т.е.:
, т.е.:
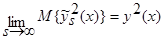 . (39)
. (39)
Таким образом, теорема 2 доказана.
Аналогично выглядит доказательство теоремы 2 для оценки функции регрессии типа оценки 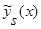 (2), когда вместо суммы двух функций
(2), когда вместо суммы двух функций 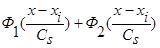 имеем сумму n функций
имеем сумму n функций 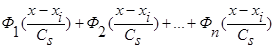 , где n>2 и все n функций удовлетворяют условиям сходимости (4) и свойству
, где n>2 и все n функций удовлетворяют условиям сходимости (4) и свойству 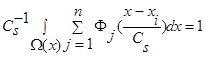 .
.
Теоремы 1 и 2 доказаны для оценок плотности распределения вероятности 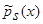 (1) и кривой регрессии
(1) и кривой регрессии 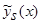 (2), когда х – скалярная величина. В случае, когда х – векторная величина, оценки плотности распределения вероятности и кривой регрессии выглядят следующим образом:
(2), когда х – скалярная величина. В случае, когда х – векторная величина, оценки плотности распределения вероятности и кривой регрессии выглядят следующим образом:
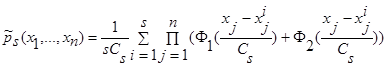 , (40)
, (40)
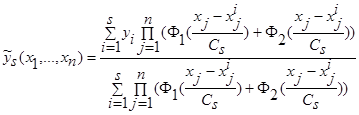 . (41)
. (41)
Теоремы 1 и 2 для оценок плотности распределения вероятности 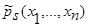 (41) и кривой регрессии
(41) и кривой регрессии 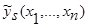 (42) имеют такую же схему доказательства, что и для оценок
(42) имеют такую же схему доказательства, что и для оценок 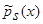 (1) и
(1) и 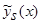 (2).
(2).
Таким образом, в данной работе приведены оценки плотности распределения вероятности 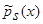 (1) и кривой регрессии
(1) и кривой регрессии 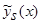 (2), предназначенные для работы в условиях А, и доказана их сходимость.
(2), предназначенные для работы в условиях А, и доказана их сходимость.
Ниже для наглядного сравнения результатов работы разных непараметрических оценок кривой регрессии представлены численные примеры.
Численное моделирование проводилось с использованием одномерных оценок кривой регрессии 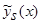 (2) и
(2) и 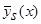 (часть 1 (5)). Истинная зависимость, неизвестная алгоритму и необходимая только для определения качества результатов оценок кривой регрессии, имеет вид:
(часть 1 (5)). Истинная зависимость, неизвестная алгоритму и необходимая только для определения качества результатов оценок кривой регрессии, имеет вид: 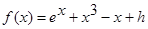 , где
, где 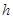 - величина, характеризующая уровень случайных помех с нулевым математическим ожиданием и ограниченной дисперсией. Исследования проводились на интервале [0,2], объем выборки s=30 точек. Выбор параметра размытости
- величина, характеризующая уровень случайных помех с нулевым математическим ожиданием и ограниченной дисперсией. Исследования проводились на интервале [0,2], объем выборки s=30 точек. Выбор параметра размытости 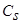 осуществлялся путем минимизации критерия:
осуществлялся путем минимизации критерия:
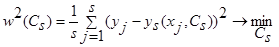 .
.
Ошибка аппроксимации 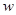 находится, как
находится, как 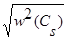 .
.
Ниже представлены результаты численного моделирования разных оценок кривой регрессии, работающих при различном уровне помех.
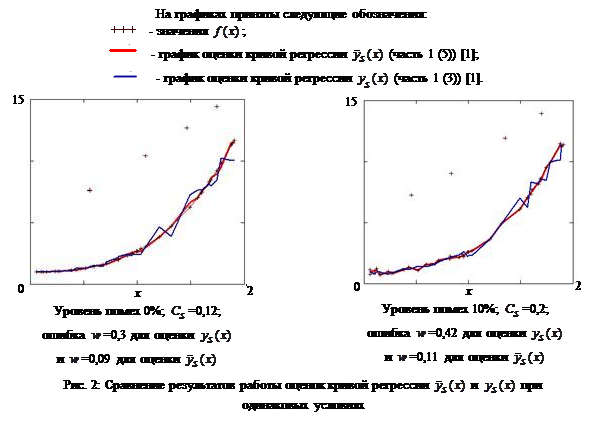
Как видно на Рис. 2, при наличии условий А в выборке «входных – выходных переменных» оценка кривой регрессии 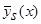 (часть 1 (5)) [1] дает результаты лучше, чем оценка
(часть 1 (5)) [1] дает результаты лучше, чем оценка 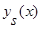 (часть 1 (3)) [1].
(часть 1 (3)) [1].
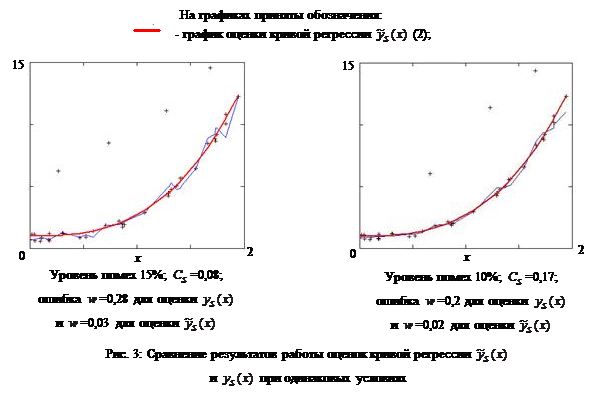 |
Как видно на Рис. 3, при наличии условий А в выборке «входных – выходных переменных» оценка кривой регрессии 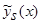 дает результаты лучше, чем оценка
дает результаты лучше, чем оценка 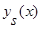 (часть 1 (3)) [1].
(часть 1 (3)) [1].
Из выше приведенных доказательств и графиков следует, что непараметрические оценки плотности распределения вероятности 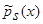 (1) и кривой регрессии
(1) и кривой регрессии 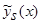 (2), а также оценки
(2), а также оценки 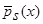 (часть 1 (4)) [1] и
(часть 1 (4)) [1] и 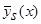 (часть 1 (5)) [1], могут быть использованы при наличии условий А. Непараметрические оценки кривой регрессии
(часть 1 (5)) [1], могут быть использованы при наличии условий А. Непараметрические оценки кривой регрессии 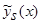 (2) и
(2) и 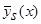 (часть 1 (5)) [1] дают лучшие результаты, чем оценка
(часть 1 (5)) [1] дают лучшие результаты, чем оценка 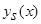 (часть 1 (3)) [1].
(часть 1 (3)) [1].
Литература
1. Демченко, Я.И. О некоторых непараметрических оценках плотности вероятности и кривой регрессии. Часть 1 // Молодой ученый – Чита, 2010.
2. Надарая, Э. А. Непараметрические оценки кривой регрессии// Некоторые вопросы теории вероятностных процессов.- АН Груз. ССР: 1965, вып. 5, с. 56 - 68.

