Моделирование дискретно-непрерывных процессов является одной из центральных проблем кибернетики. Ниже рассматриваются непрерывные во времени процессы, но входные и выходные переменные доступны измерению в дискретные моменты времени. Проиллюстрируем схему такого процесса на Рис. 1:
Здесь приняты обозначения: 
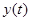- векторная выходная переменная процесса, 
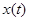- векторное управляющее воздействие, 
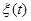- векторное случайное воздействие, (
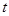) – непрерывное время, 
, 
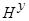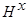– каналы связи, соответствующие различным переменным, включающие в себя средства контроля, приборы для измерения наблюдаемых переменных, 
,
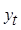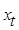- измерения в дискретные моменты времени. Контроль переменных 
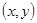осуществляется через интервал времени 
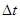, т.е. 
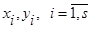- выборка статистически независимых измерений переменных процесса 
, 
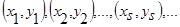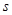- объем выборки, 
,
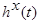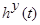– случайные помехи измерений соответствующих переменных процесса.
Задача идентификации дискретно-непрерывных процессов состоит в построении их математической модели, например, на основе непараметрических оценок функции регрессии по наблюдениям. В свою очередь, непараметрические оценки функции регрессии базируются на непараметрических оценках плотности вероятности. В дальнейшем на это и будет сделан основной акцент. Причем, мы учитываем тот факт, что имеющиеся выборки в пространстве «входных – выходных» переменных в реальности расположены неравномерно. Настоящее исследование посвящено непараметрическим оценкам плотности вероятности и функции регрессии, отличающимся от известных, а именно, когда выборка (x1,y1), (x2y2), … , (xs,ys) расположена некоторым характерным образом, определяемым реальной ситуацией, с которой часто приходится сталкиваться на практике. Это обусловлено следующими чертами:
1. сгущением значений измеряемых параметров на некоторых участках интервала измерения;
2. пустотами – отсутствием значений измеряемых параметров на некоторых участках интервала измерения;
3. разреженностью – наличием нескольких значений измеряемых параметров, распределенных по интервалу неравномерно.
Назовем условия 1, 2, 3 условиями А.
Сначала рассмотрим непараметрическую оценку плотности вероятности по наблюдениям и изучим асимптотические свойства этой оценки.
Пусть (x,y) – случайная величина со значениями в пространстве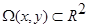 
, а p(x,y)>0 – плотность распределения двумерной случайной величины (x,y), она неизвестна. Пусть (x1,y1), (x2y2), … , (xs,ys) – выборка из s статически независимых наблюдений двумерной случайной величины (x,y).
Обычно в качестве непараметрической оценки плотности вероятности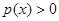 
принимают статистику [1,2]:
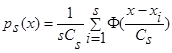, (1)
где интегрируемая с квадратом функция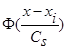 
и параметр Cs(коэффициент размытости) таковы, что удовлетворяют условиям сходимости [3]:
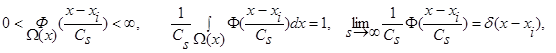
(2)
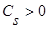, s=1,2,… , 
, 
.
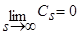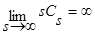Назовем условия сходимости (2) условиями В.
Непараметрической оценкой функции регрессии - М(у/х) является:
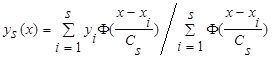, (3)
где знаменатель -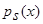 
(1) с точностью до 
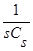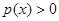, , а числитель обозначим 
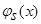. Асимптотические свойства непараметрических оценок плотности вероятности (1) и кривой регрессии (3), а также их функционалов, подробно исследовались в [4].
При наличии условий А в выборке наблюдаемых переменных предлагается использовать новые непараметрические оценки плотности распределения вероятности следующего вида:
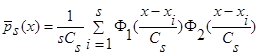(4)
и кривой регрессии:
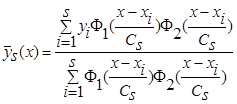, (5)
где знаменатель является оценкой плотности распределения вероятности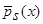
(4) с точностью до , 
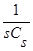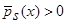, числитель же обозначим:
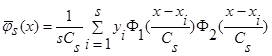, (6)
а функции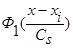 
, 
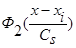четные относительно 
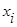и, например, имеют вид:
, 
,
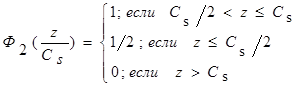здесь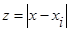 
.
Для непараметрической оценки плотности вероятности 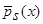(4) имеет место следующая теорема:
Теорема 1. Пусть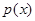 
дважды дифференцируема, а функции 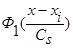, 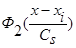и параметр размытости 
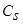удовлетворяют условиям сходимости В и свойству 
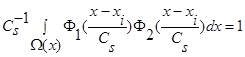, тогда:
, 
.
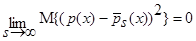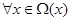Доказательству теоремы 1 предпошлем следующую лемму.
Лемма 1.1. Непараметрическая оценка плотности распределения вероятности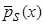 
в условиях теоремы 1 является асимптотически несмещенной.
Доказательство леммы 1.1. Возьмем математическое ожидание от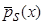 
(4):
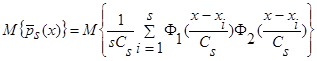. (7)
Воспользуемся свойствами математического ожидания и получим:
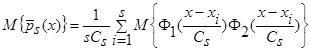, (8)
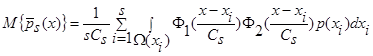. (9)
Поскольку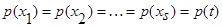 
, то имеем s одинаковых интегралов:
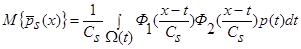. (10)
Сделаем замену переменных:
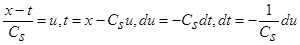, (11)
и, учитывая, что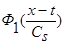 
и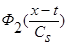 
- четные функции относительно 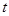, из выражения (10) получаем:
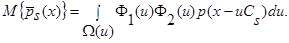(12)
Далее разложим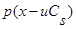 
в ряд Тейлора с остаточным членом в форме Лагранжа [2]:
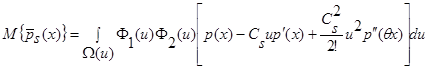, (13)
где 0<θ<1 – некоторая константа.
Воспользуемся свойствами интегралов, тогда:
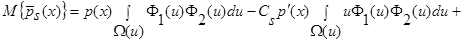
(14)
.
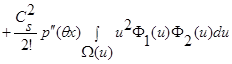Применим свойства функций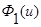 
и 
и 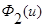параметра размытост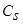и при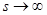 
:
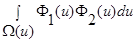=1, остальные слагаемые обращаются в ноль, поскольку 
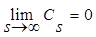. Следовательно:
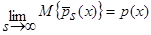. (15)
То есть, оценка функции плотности распределения вероятности 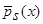(4) является асимптотически несмещенной. Таким образом, лемма 1.1 доказана.
Аналогично выглядит доказательство асимптотической несмещенности оценки плотности распределения вероятности типа оценки 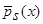(4), когда вместо произведения двух функций 
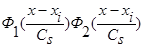имеем произведение n функций 
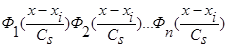, где n>2 и все n функций удовлетворяют условиям сходимости В и свойству 
.
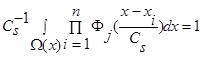Доказательство теоремы 1. Возьмем математическое ожидание от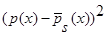 
и при 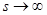получим:
.
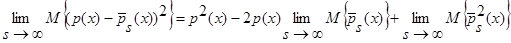С учетом леммы 1.1 имеем:
.
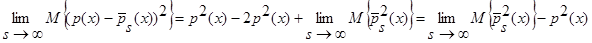Докажем, что:
.
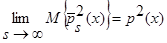Вычислим математическое ожидание от квадрата оценки плотности распределения вероятности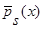 
(4):
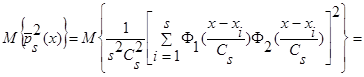
(16)
.
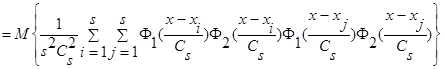Двойная сумма разбивается на два слагаемых, первое – когда i=j, второе - когда i≠j, поскольку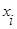 
и 
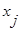статистически независимы, то есть 
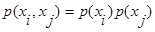, тогда:
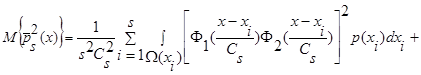
(17)
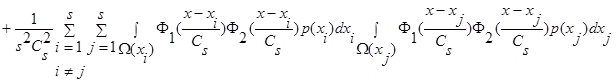
Так, как 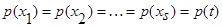, то:
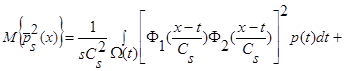
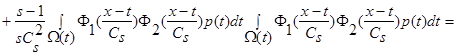(18)
.
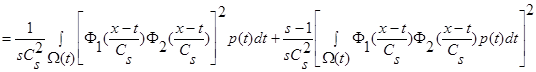Сделаем замену переменных (11): 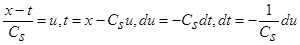, и, учитывая, что 
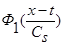и 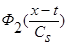- четные функции относительно 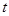, получаем:
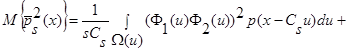
(19)
.
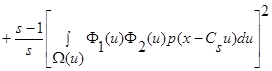При 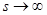интеграл 
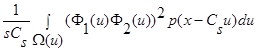стремится к нулю, поскольку 
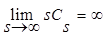, следовательно:
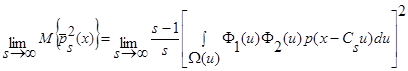. (20)
С учетом условий сходимости и при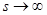 
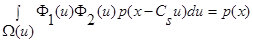(см. (12) – (15)), то есть:
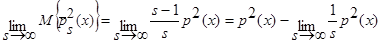. (21)
Так, как s→∞, то 
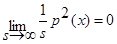. В итоге получаем:
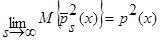. (22)
Тогда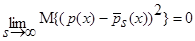 
. Таким образом, теорема 1 доказана.
Аналогично выглядит доказательство теоремы 1, когда в оценке плотности распределения вероятности, типа оценки 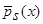(4), вместо произведения двух функций 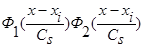имеем произведение n функций 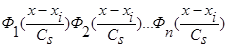, где n>2 и все n функций удовлетворяют условиям сходимости В и свойству 
.
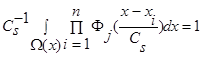Для непараметрической оценки кривой регрессии по наблюдениям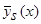 
(5) имеет место следующая теорема:
Теорема 2. Пусть 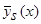дважды дифференцируема и с вероятностью единица 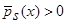,,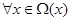 а функции 
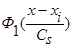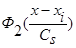, и параметр размытости 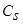удовлетворяют условиям сходимости В и свойству 
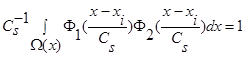, тогда:
, .
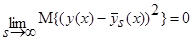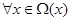Рассмотрим следующее тождество [5]:
.
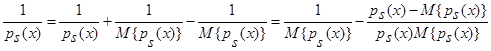Умножим обе части выражения на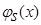 
и возьмем от полученного выражения математическое ожидание:
.
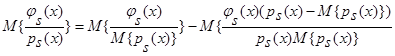Поскольку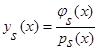 
, а в знаменателях слагаемых при фиксированном x 
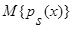является константой и ее можно вынести за знак математического ожидания, то:
.
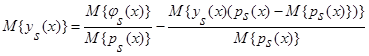При s→∞ имеем:
.
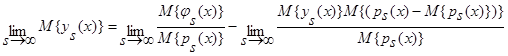Слагаемое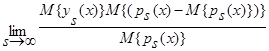 
в силу независимости наблюдений 
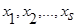и ограниченности функций обращается в ноль. Следовательно:
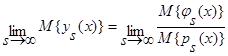. (23)
Доказательству теоремы 2 предпошлем леммы 2.1, 2.2 для оценки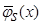 
(6) и лемму 2.3 для оценки регрессии 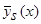(5).
Лемма 2.1. Непараметрическая оценка функции 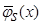в условиях теоремы 2 является асимптотически несмещенной.
Доказательство леммы 2.1. Вычислим математическое ожидание от 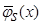(6):
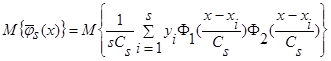. (24)
Произведя в выражении (24) простые преобразования, получим:
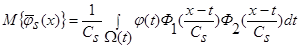. (25)
Сделаем замену переменных (11): 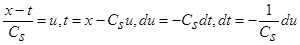, и, учитывая, что 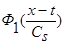и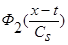 
- четные функции относительно 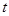, получаем:
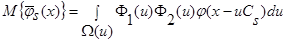. (26)
Далее разложим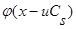 
в ряд Тейлора с остаточным членом в форме Лагранжа:
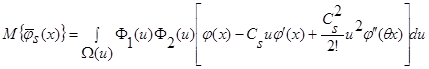, (27)
где 0<θ<1 – некоторая константа.
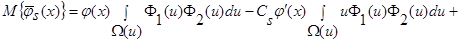
(28)
.
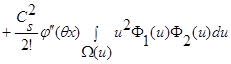Применим свойства функций 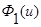и и 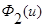параметра размытости 
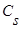при :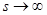
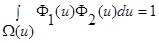, остальные слагаемые обращаются в ноль, поскольку 
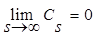. Следовательно:
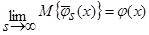. (29)
То есть, оценка 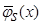(6) является асимптотически несмещенной.
Таким образом, лемма 2.1 доказана.
Аналогично выглядит доказательство асимптотической несмещенности оценки функции типа оценки 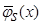(6), когда вместо произведения двух функций 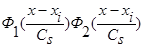имеем произведение n функций 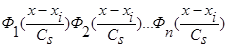, где n>2 и все n функций удовлетворяют условиям сходимости В и свойству .
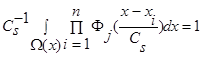Лемма 2.2. Пусть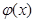 
дважды дифференцируема, а функции 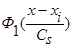, 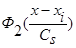и параметр размытости 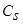удовлетворяют условиям сходимости В и свойству 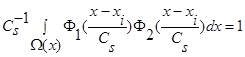, тогда:
, .
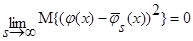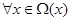Доказательство леммы 2.2. Возьмем математическое ожидание от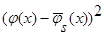 
и при 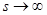получаем:
.
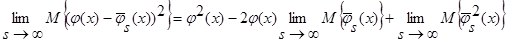С учетом леммы 2.1 имеем:
.
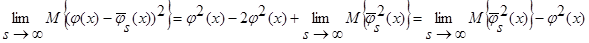Докажем, что:
.
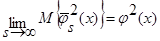Вычислим математическое ожидание от квадрата оценки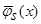 
(6):
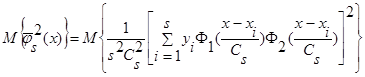. (30)
Произведя в выражении (30) простые преобразования и учитывая, что 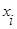и 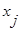статистически независимы, то есть 
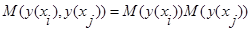, получим:
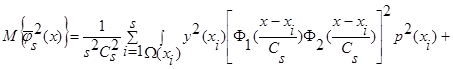
(31)
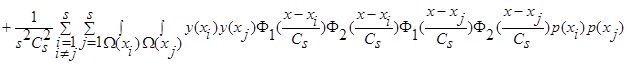
В силу обозначений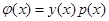 
и поскольку 
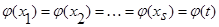то:
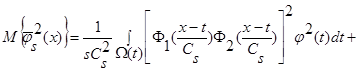
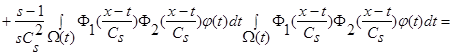(32)
.
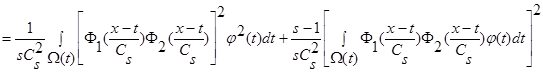Сделаем замену переменных (11): 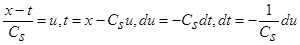, и, учитывая, что 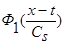и 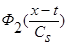- четные функции относительно 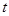, получаем:
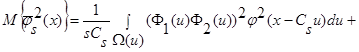
(33)
.
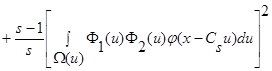При 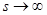интеграл 
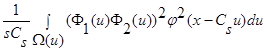стремится к нулю, поскольку 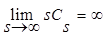, следовательно:
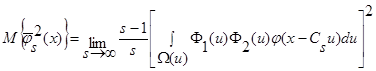. (34)
С учетом условий сходимости и при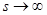 
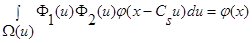(см. (26) – (29)), то есть:
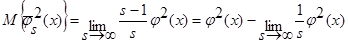. (35)
Так, как s→∞,то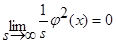 
. В итоге имеем:
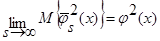. (36)
Таким образом, лемма 2.2 доказана.
Аналогично выглядит доказательство леммы 2.2 для оценки функции типа оценки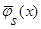 
(6), когда вместо произведения двух функций 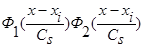имеем произведение n функций 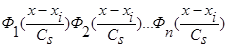, где n>2 и все n функций удовлетворяют условиям сходимости В и свойству .
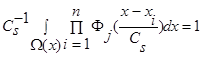Лемма 2.3. Непараметрическая оценка регрессии 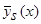в условиях теоремы 2 является асимптотически несмещенной.
Доказательство леммы 2.3. Возьмем математическое ожидание от оценки регрессии 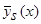(5):
.
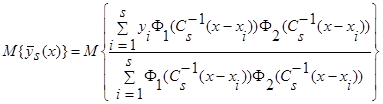С учетом (23) при 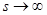, получим:
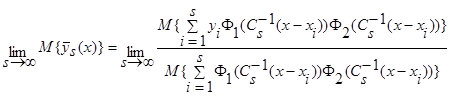. (37)
Поскольку числитель выражения (37) представляет собой математическое ожидание от оценки 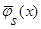(6), с учетом леммы 2.1 
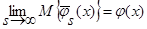(см. (24) – (29)), а знаменатель – математическое ожидание от оценки плотности распределения вероятности 
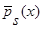(4), с учетом леммы 1.1 
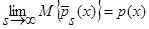(см. (7) – (15)), тогда:
.
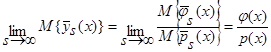В силу обозначений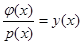 
, т.е. оценка регрессии 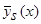(5) является асимптотически несмещенной:
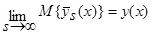. (38)
Таким образом, лемма 2.3 доказана.
Аналогично выглядит доказательство леммы 2.3 для оценки функции регрессии типа оценки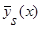 
(6), когда вместо произведения двух функций 
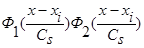имеем произведение n функций 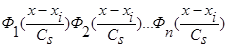, где n>2 и все n функций удовлетворяют условиям сходимости В и свойству .
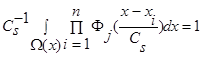Доказательство теоремы 2. Возьмем математическое ожидание от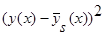 
и при 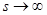получим:
,
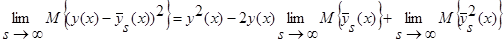С учетом леммы 2.3 имеем:
.
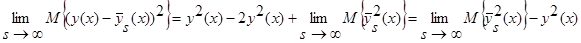Докажем, что:
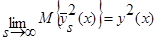. (39)
Вычислим математическое ожидание от квадрата оценки регрессии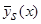 
(5):
.
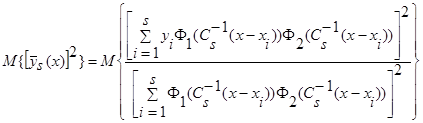С учетом (23) при 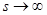, получим:
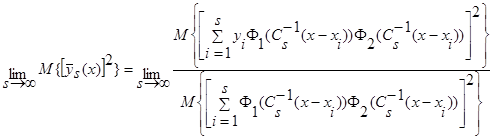. (40)
Поскольку числитель выражения (40) представляет собой математическое ожидание от квадрата оценки 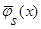(6), с учетом леммы 2.2 
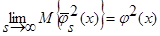(см. (30) – (36)), а знаменатель – математическое ожидание от квадрата оценки плотности распределения вероятности 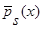(4), с учетом теоремы 1 
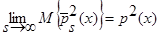(см. (16) – (22)), тогда:
.
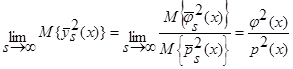В силу обозначений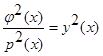 
, т.е.:
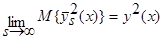. (41)
Таким образом, теорема 2 доказана, с учетом леммы 2.2, теоремы 1 и выражения 23.
Аналогично выглядит доказательство теоремы 2 для оценки функции регрессии типа оценки 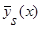(6), когда вместо произведения двух функций 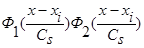имеем произведение n функций 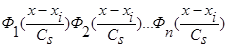, где n>2 и все n функций удовлетворяют условиям сходимости B и свойству .
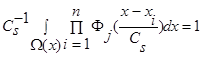Теоремы 1 и 2 доказаны для оценок плотности распределения вероятности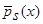 
(4) и кривой регрессии 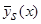(5), когда х – скалярная величина. В случае, когда х – векторная величина, оценки плотности распределения вероятности и кривой регрессии выглядят следующим образом:
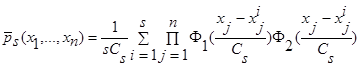, (42)
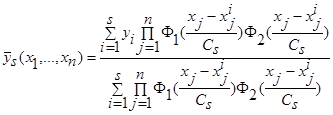. (43)
Теоремы 1 и 2 для оценок плотности распределения вероятности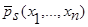 
(42) и кривой регрессии 
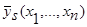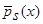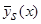(43) имеют такую же схему доказательства, что и для оценок (4) и (5).
Таким образом, в данной работе приведены оценки плотности распределения вероятности 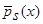(4) и кривой регрессии 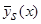(5), предназначенные для работы в условиях А, с которыми часто приходится сталкиваться на практике, и доказана их сходимость. Новые непараметрические оценки кривой регрессии являются более устойчивыми к разреженности, пустотам и выбросам в пространстве «входных - выходных» значений, чем оценки 
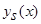(5), и в этих условиях позволяют аппроксимировать искомый процесс.
Литература:
1. Parzen, E. On estimation of a probability density.//Ann. Maht. Statistic, 1969, N 3, p. 854-864.
2. Епанечников, В.А. Непараметрическая оценка многомерной плотности вероятности // Теория вероятностей и ее применение – 1969, т. 14, вып. 1, с 156-162.
3. Медведев, А.В. Непараметрические системы адаптации. – Новосибирск: Наука, 1983.
4. Васильев, В.А. Непараметрическое оценивание функционалов от распределений стационарных последовательностей / В.А. Васильев, А.В. Добровидов, Г.М. Кошкин. М.: Наука, 2004. 508с.
5. Надарая, Э. А. Замечания о непараметрических оценках плотности вероятности и кривой регрессии // Теория вероятности и ее применение.- Т. 15, вып. 1, 1970.-с. 139-142.
