Ключевые слова: физическая теория, дедуктивные следствия теоретического ядра, теоретическое мышление
Физика является основой формирования научных знаний о природе, на ее основе формируется мировоззрение обучающихся среднего профессионального образования. Усвоение в дальнейшем технических наук во многом зависит от системности и фундаментальности физико-математического образования.
Систематизация материала курса физики на основе фундаментальных физических теорий и идеи научной картины мира служит реализации единства системы знаний и методов научного познания, а также основой формирования системных научных знаний, развития научного мышления обучающихся.
В физических теориях отражаются результаты научного стиля мышления, воплощаются в свернутом виде элементы цикла познания. Каждая из физических теорий исследует свой фрагмент природы, содержательная структура всех физических теорий одинакова.
Cодержательная структура физической теории как концептуальной системы состоит из диалектически взаимосвязанных элементов: эмпирического основания теории; концептуального теоретического ядра теории; дедуктивного теоретического следствия.
Важнейшим признаком научного знания является его принципиальная проверяемость. Следует подчеркнуть, основные законы физической теории не поддаются непосредственной эмпирической проверке — проверке практикой. Экспериментальной проверке техническими средствами подвергаются дедуктивные следствия теоретического ядра, что подтверждает (или опровергает) истинность ядра физической теории.
Примерами дедуктивных следствий теоретического ядра классической механики являются: «Элементы динамики вращательного движения твердого тела. Элементы статики. Элементы гидростатики и гидродинамики. Элементы теории механических колебаний и волн». Они служат иллюстрацией применения основных законов к конкретным механическим системам. Для них вводятся более сложные модели: упругое тело, пластическое тело, несжимаемая жидкость и др. Через теоретические следствия, дедуктивно выведенные из фундаментальных законов, реализуется объяснительная и предсказательная функции физической теории.
В окружающем нас мире и технике часто приходится сталкиваться с периодическими (или почти периодическими) процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени называют механическими колебаниями. При изучении колебаний рассматривают свойства различных колебательных систем. Примерами простых колебательных систем могут служить груз на пружине или математический маятник Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными.
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными. Простейшим видом колебательного процесса являются простые гармонические колебания, в которых динамическая переменная ![]() описываются уравнением с использованием функций синуса (косинуса)
описываются уравнением с использованием функций синуса (косинуса) ![]() . При этом колебательная система, как материальный объект, называется гармоническим осциллятором. Элементы теории механических колебаний рассмотрим как пример дедуктивного следствия ядра физической теории «Механика Ньютона». При описании процессов, происходящих в колебательных системах, мы иллюстрируем применение основных законов к конкретным механическим системам.
. При этом колебательная система, как материальный объект, называется гармоническим осциллятором. Элементы теории механических колебаний рассмотрим как пример дедуктивного следствия ядра физической теории «Механика Ньютона». При описании процессов, происходящих в колебательных системах, мы иллюстрируем применение основных законов к конкретным механическим системам.
Рассмотрим на примере колеблющегося груза на пружине применение второго закона Ньютона для вывода уравнения движения. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f(t). Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Выбираем инерциальную систему координат, связанную с Землей, приняв за начало координат положение равновесия тела. Втрой закон Ньютона ![]() трансформируется:
трансформируется: ![]() , где
, где ![]() — это упругая сила, определяемая законом Гука:
— это упругая сила, определяемая законом Гука: ![]() . Следовательно,
. Следовательно, ![]() , откуда
, откуда ![]() . Или
. Или![]() Решением этого дифференциального уравнения второго порядка является гармоническая функция:
Решением этого дифференциального уравнения второго порядка является гармоническая функция: ![]() Пружинный маятник является примером гармонического осциллятора. В качестве возвращающей силы не обязательно должна быть сила упругости. Например, для математического маятника — это равнодействующая сил тяжести и упругости. Периодическая функция времени x = f(t), позволяет предсказать состояние колебательной системы со временем. Так реализуется предсказательная функция физической теории для конкретной механической системы.
Пружинный маятник является примером гармонического осциллятора. В качестве возвращающей силы не обязательно должна быть сила упругости. Например, для математического маятника — это равнодействующая сил тяжести и упругости. Периодическая функция времени x = f(t), позволяет предсказать состояние колебательной системы со временем. Так реализуется предсказательная функция физической теории для конкретной механической системы.
Для получения уравнений скорости и ускорения нужно применить закон изменения первой и второй производной. Тогда уравнение скорости
При изучении колебательных процессов важно использовать закон сохранения импульса и особенно закон сохранения энергии, которые входят с состав ядра механики Ньютона. С энергетической точки зрения колебательный процесс представляет собой периодический обмен энергией между различными элементами системы и превращение энергии одного вида, например кинетической, в другой вид энергии, например потенциальную.
Покажем, что для любого положения колеблющегося тела его полная энергия не изменяется в процессе колебаний на примере груза, совершающего свободные гармонические колебания на достаточно жесткой пружине.
Закон изменения кинетической энергии:
![]() , где
, где ![]() — максимальное значение кинетической энергии груза.
— максимальное значение кинетической энергии груза.
Закон потенциальной энергии:
![]() , где
, где
![]() – максимальная потенциальная энергия пружины.
– максимальная потенциальная энергия пружины.
Кинетическая и потенциальная энергии изменяются с частотой 2ω, то есть в два раза большей, чем частота колебаний координаты. Сравнивая выражения для изменения потенциальной и кинетической энергий, видим, что энергии изменяются в противофазе. При свободных гармонических колебаниях собственная частота осциллятора ![]() , следовательно,
, следовательно, ![]() . Полная механическая энергия не изменяется в процессе колебаний:
. Полная механическая энергия не изменяется в процессе колебаний: ![]() .
.
Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.
Приведем пример методики решения задачи на основе аналогии между механическими и электрическими колебаниями.
Задача. Найти период колебаний осцилляторов, изображенных на схеме 1 и 2.
Для решения такой задачи следует перейти к эквивалентной электрической системе. Двум пружинам механического осциллятора в электрической системе соответствуют два конденсатора, имеющие емкости![]() и
и ![]() , а массе — индуктивность L. Как должны будут соединены конденсаторы, следует дополнительно конкретизировать. В первом случае при смещении груза m на некоторое расстояние (х) каждая из пружин получит такое же удлинение (
, а массе — индуктивность L. Как должны будут соединены конденсаторы, следует дополнительно конкретизировать. В первом случае при смещении груза m на некоторое расстояние (х) каждая из пружин получит такое же удлинение (![]() и
и![]() ): х =
): х =![]() =
=![]() . Так как смещению х соответствует заряд q, то конденсаторы следует соединить последовательно, поскольку при этом q=
. Так как смещению х соответствует заряд q, то конденсаторы следует соединить последовательно, поскольку при этом q=![]() =
=![]() . Таким образом, получаем эквивалентную схему (рис)и далее находим период электрических колебаний:
. Таким образом, получаем эквивалентную схему (рис)и далее находим период электрических колебаний: ![]() , где
, где ![]() . Далее используя аналогию, запишем период колебаний механического осциллятора:
. Далее используя аналогию, запишем период колебаний механического осциллятора: 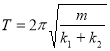 .
.
Дедуктивные следствия, как теоретические обобщения второго уровня проверяются практикой. Экспериментальная проверка техническими средствами подтверждает (или опровергает) истинность ядра физической теории. Теория колебаний многократно проверена на практике и нашла широкое применение в различных технологических процессах и машинах. Примером могут служить сортировочные машины, вибрационные конвейеры, вибролитье, виброрезание и т. д. Приходится учитывать и вредное действие колебаний. Понимание природы колебаний, умение правильно выбрать динамическую модель машины, адекватную колебательным процессам, оценить виброактивность механизмов и машины в целом, знание методов уменьшения виброактивности и методов виброзащиты машин, аппаратов, людей, а также способов полезного использования колебаний в рабочих процессах совершенно необходимы для будущего специалиста направления подготовки 18.01.27 Машинист технологических насосов и компрессоров (МТНр).
Таким образом, знание логического генезиса дедуктивных следствий физической теории служит формированию системности знаний физических теорий, развитию теоретического мышления обучающихся.
Литература:
- Казаков, Р. Х. Методическая система обучения общей физике в педагогическом вузе /Р. Х. Казаков. — М.: МГОУ, 2003. — 84с.
- Половникова Л. Б. Методическая система преемственности курса физики технического вуза (на примере вводного раздела «Механика»): Автореф. дис. канд. пед. наук. — Тюмень, 2009. — 24 с.







