В данной работе в приближенном виде найдены зависимости периода колебаний одномерного релятивистского гармонического осциллятора от его амплитуды колебаний и полной механической энергии. Также приведено сравнение полученных результатов с известным периодом колебаний гармонического осциллятора в классическом случае.
Ключевые слова: релятивистский гармонический осциллятор, финитное движение, зависимость периода от энергии, зависимость периода от амплитуды, изохронность
Известно, что в рамках классической механики гармонические колебания частицы (гармонического осциллятора) обладают свойством изохронности [1], т. е. период таких колебаний не зависит от их амплитуды. Впрочем, изохронность гармонических колебаний в классическом случае сохраняется до тех пор, пока выполнено требование малости таких колебаний, при учете следующих членов в разложении потенциальной энергии частицы появляется зависимость периода от ее амплитуды колебаний.
Переход же от классической механики к релятивистской при описании движения частицы во внешних потенциальных полях в свою очередь приводит к появлению релятивистских эффектов и более сложным зависимостям между исследуемыми величинами, которые, однако, не всегда можно получить в точном виде. Возможность получения точных выражений для периода финитного движения частицы в некоторых симметричных внешних потенциальных полях обсуждалась в [2]. В настоящей работе в первых двух приближениях получены простые выражения для зависимостей периода колебаний релятивистского осциллятора во внешнем квадратичном потенциальном поле от его амплитуды колебаний и полной энергии.
Рассмотрим релятивистскую частицу массой покоя ![]() , которая может совершать одномерное финитное движение во внешнем поле с потенциальной энергией
, которая может совершать одномерное финитное движение во внешнем поле с потенциальной энергией ![]() , где
, где ![]() — коэффициент квазиупругой силы, действующей на частицу,
— коэффициент квазиупругой силы, действующей на частицу, ![]() — ее координата. Будем считать внешнее поле стационарным, поэтому сохраняется полная энергия
— ее координата. Будем считать внешнее поле стационарным, поэтому сохраняется полная энергия ![]() релятивистской частицы в данном поле, которую можно представить в следующем виде [3]
релятивистской частицы в данном поле, которую можно представить в следующем виде [3]
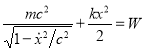 ,
,
где первое слагаемое — это энергия движения свободной релятивистской частицы, ![]() — ее скорость,
— ее скорость, ![]() — скорость света в вакууме.
— скорость света в вакууме.
Проинтегрируем это уравнение, разделяя переменные, в результате получим выражение для периода финитного движения ![]() в зависимости от полной энергии релятивистской частицы
в зависимости от полной энергии релятивистской частицы ![]() в виде
в виде
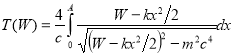 , (1)
, (1)
где
![]() , (2)
, (2)
другими словами, наибольшее отклонение частицы при данной энергии ![]() или амплитуда колебаний.
или амплитуда колебаний.
Преобразуем подынтегральное выражение в (1) с учетом (2) к следующему виду
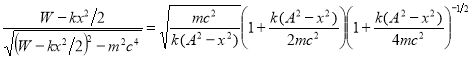 . (3)
. (3)
Далее, для того чтобы упростить вычисление интеграла в (1), будем считать потенциальную энергию малой по сравнению с энергией покоя частицы, так что можно разложить последний множитель в выражении (3) в ряд:

При этом мы ограничимся первыми тремя членами разложения, тем самым получим искомое выражение для периода колебаний осциллятора с учетом релятивистских поправок до второго порядка включительно. В результате разложения выражение (3) примет вид
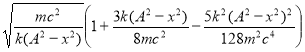 . (4)
. (4)
Тогда, вычисляя интеграл (1) с уже выражением (4), после преобразований получим в первых двух приближениях следующую зависимость периода колебаний релятивистского гармонического осциллятора от его амплитуды колебаний:
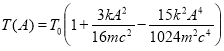 , (5)
, (5)
где
Используя связь энергии и амплитуды (2), из (5) нетрудно получить соответственно зависимости периода колебаний релятивистского осциллятора от его полной энергии в первом приближении
![]() (6)
(6)
и во втором
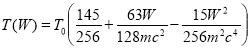 , (7)
, (7)
где так же считается, что полная энергия ![]() релятивистской частицы не сильно отличается от ее энергии покоя.
релятивистской частицы не сильно отличается от ее энергии покоя.
Таким образом, расчет и анализ периода колебаний релятивистского гармонического осциллятора показал, что по сравнению с классическим случаем изохронность колебаний релятивистского осциллятора нарушается: в силу релятивистских эффектов в первом приближении появляется квадратичная зависимость периода от амплитуды, во втором приближении — зависимость четвертой степени от амплитуды колебаний осциллятора (формула (5)). Кроме этого, различны зависимости периода такого осциллятора от его полной энергии в первом и втором приближениях (формулы (6) и (7) соответственно).
В заключение отметим, что рассмотренная методика приближенного вычисления периода колебаний релятивистского гармонического осциллятора позволяет также получить приближения и более высоких порядков.
Литература:
- Сивухин Д. В. Общий курс физики. Т. 1. Механика. — М., 2005. — 560 с.
- Кочкин С. А., Фофанов А. С. Зависимости периода одномерного финитного движения релятивистской частицы от ее полной энергии и амплитуды во внешних потенциальных полях // Молодой ученый. — 2017. — № 5(139). — С. 17–19.
- Истеков К. К. Курс теоретической физики. — А., 2005. — 574 с.







