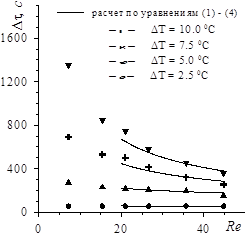В работе представлены результаты экспериментального исследования нестационарного теплообмена при циклической фильтрации потока воздуха через зернистый слой, в качестве которого использовали свинцовые (D= 2.0, 3.5 и 4.5 мм) и стеклянные шары (D = 3.2 мм). Для исследованных засыпок измерена зависимость времени переключения направления потока воздуха от числа Рейнольдса. Разработана математическая модель процесса, описывающая теплообмен между газовым потоком и неподвижным слоем шаров. Хорошее согласование экспериментальных данных с расчетными наблюдается при больших числах Рейнольдса, в то время как при малых сказывается влияние тепловых потерь, в результате чего экспериментальное время оказывается меньше расчетного. Полученные результаты могут быть использованы при разработке регенеративных тепло- массообменных устройств.
1. Введение
Известны определенные нестационарные режимы проведения каталитических реакций, значительно превосходящие по своей эффективности стационарные. Одним из способов реализации такого режима может быть переключение направления подачи газа в слой катализатора [1, 2]. Исследования [3, 4] показывают, что такая организация химических реакций позволяет удерживать зону с высокой температурой внутри зернистого слоя при низкой входной температуре. В этом случае наличие катализатора позволяет не только увеличивать скорость реакции, но и выполнять роль регенератора теплоты, т.е. дает возможность осуществлять химические реакции (например, окисление диоксида серы, синтез аммиака) без дополнительного подвода энергии. Реверсивные режимы без адсорбции газа или его химической реакции с материалом слоя исследуются в регенеративных теплообменниках для нагрева воздуха с непористыми теплоаккумулирующими элементами. В качестве таких элементов для утилизации высокотемпературной теплоты используют огнеупорные насадки (например, кирпич).
В данной работе экспериментальными и численными методами исследованы реверсивные режимы фильтрации воздуха через слой теплоаккумулирующей среды, в которых коэффициенты теплоотдачи от поверхности зерна имеют невысокие значения, и термическое сопротивление на внешней поверхности является основным. Именно такие режимы реализуются в недавно предложенном устройстве для регенерации теплоты и влаги в системе вентиляции бытовых и офисных помещений [5].
2. Экспериментальная установка
Опыты проводили на установке, подробно описанной в [6]. Рабочий участок представлял собой полиэтиленовую трубу диаметром 210 мм и длиной 800 мм. Внутрь трубы помещали кассеты с теплоаккумулирующим материалом - свинцовыми (D = 2.0, 3.5 и 4.5 мм) и стеклянными шарами (D = 3.2 мм). Общая длина слоя шаров составляла 166 мм. Источником воздуха служил сжатый воздух из лабораторной сети. Для создания потока холодного воздуха (Т = -5 ¸ -20 оС) применяли трубку Ранка. Такая схема позволяла независимо регулировать температуру и объемную скорость воздуха на входе в устройство. Среднемассовую температуру воздуха измеряли хромель-копелевыми термопарами, показания которых автоматически регистрировали. Для уменьшения тепловых потерь кассеты изолировали, также был теплоизолирован корпус от окружающей среды.
Реверсивные режимы теплообмена (регенерации теплоты) осуществляли по двум методикам. В первой методике переключение потока воздуха проводили следующим образом: в каждом нечетном полуцикле при достижении фиксированного падения температуры DТТ на теплом конце регенератора, а в каждом четном - по длительности предыдущего нечетного полуцикла. По второй методике переключение осуществляли при достижении фиксированного падения температуры на теплом DТТ и холодном DТХ концах регенератора (DТТ = DТХ).
Первая методика заключалась в том, что на холодный вход установки подавали воздух при температуре ТХ = -8 оС. Проходя через засыпку шаров, воздух нагревался до ТТ = 20.5 оС (исходной температуры засыпки). По мере охлаждения шаров температура воздуха на теплом конце начинала постепенно снижаться. Когда она уменьшалась на заданную величину DТТ = 2.5, 5.0, 7.5 или 10.0 оС (через время Dt1), то направление потока переключали. На теплый вход подавали воздух при ТТ = 20.5 оС и продували его в течении такого же времени Dt1. Затем поток вновь переключали, и на холодный вход регенератора подавали воздух при ТХ = -8 оС. Через время Dt2 < Dt1, когда температура воздуха на теплом конце регенератора понижалась на DТТ = 2.5, 5.0, 7.5 или 10.0 оС, направление потока снова переключали и т.д. Вторая методика отличалась от первой тем, что потоки переключали, когда падение температуры, как на теплом, так и холодном конце регенератора достигало заданной величины DТ = 2.5, 5.0, 7.5 или 10.0 оС.
При переключении по первой методике перепад температур на холодном конце оказывался гораздо больше, чем на теплом. Это соответствует "проскоку" части теплого воздуха и уменьшению степени регенерации теплоты. Так, для свинцовых шаров при DТ = 2.5 °С коэффициент теплоутилизации по второй методике оказался равным 0.91 вместо 0.88 по первой. Если по второй методике увеличить перепад температуры до величины, которая соответствует коэффициенту теплоутилизации 0.88, то время полуцикла возрастет до 96 секунд, т.е. увеличится на 13 % по сравнению с первой методикой [6]. Таким образом, вторая методика переключения воздушных потоков приводит к повышению коэффициента теплоутилизации и к увеличению времени полуцикла.
Обобщенные графики зависимости времени полуцикла от числа Re для исследованных засыпок представлены на Рис. 1-2. При близких размерах, время полуцикла для стеклянных шаров примерно в 1.5-2.5 раза больше, чем для свинцовых. Это в основном связано с большей объемной теплоемкостью стекла (1960 кДж/(м3×К)) по сравнению со свинцом (1450 кДж/(м3×К)), которые отличаются в 1.35 раза. Некоторое дополнительное уменьшение времени полуцикла для свинцовых шаров может быть связано тем, что их теплопроводность l больше, чем у стеклянных. В результате возрастает поток тепла в слой шаров через стенки установки из окружающей среды, и слой прогревается быстрее, чем при его нагреве только фильтрующимся воздухом. Этот эффект особенно заметен при малых потоках, которым соответствуют большие времена контакта воздуха с засыпкой.
Таким образом, в качестве теплоаккумулирующей среды перспективно использовать материалы с высокой теплоемкостью и относительно низкой теплопроводностью, которая, тем не менее, должна быть достаточной, чтобы обеспечить быструю передачу теплоты от внешней поверхности в объем отдельной частицы среды. Это условие выполняется, если термическое сопротивление внутри единичной частицы засыпки (условно в форме шара радиуса R), которое можно оценить как R/l, гораздо меньше, чем термическое сопротивление при передаче теплоты от воздуха к внешней поверхности шара 1/a. При a » 50 Вт/(м2∙К) и R = 2×10-3 м, достаточно, чтобы теплопроводность материала теплоаккумулирующей среды была гораздо больше 0.01 Вт/(м×К), что с запасом выполняется для стекла (l = 1.1 Вт/(м×К)).
Характер изменения времени полуцикла в зависимости от Re и ΔТ для свинцовых шаров диаметром 2.0 и 4.5 мм практически одинаков: при малых ΔТ время полуцикла слабо зависит от Re, в то время как при больших ΔТ оно резко уменьшается с увеличением числа Re (рис.1 и 2). Вместе с тем следует отметить, что время полуцикла для шаров диаметром 2.0 мм несколько больше (от 5 до 58%) по сравнению с шарами диаметром 4.5 мм. Это можно объяснить более высоким значением коэффициента теплоотдачи при меньшем диаметре шара (приблизительно на 24%), что, соответственно, делает тепловой фронт более резкими.
3. математическая модель реверсивного теплообмена
Теплообмен между газовым потоком и неподвижным слоем зернистого материала описывается системой уравнений [7]:
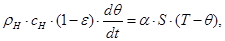(1)
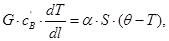(2)
с начальными и граничными условиями:
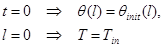
Для описания циклического процесса, реализованного в эксперименте, использовали процедуру реверса потока, которая описывается операцией:
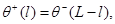(3)
где 
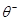и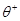 
соответствуют распределению температур до и после переключения потока, L – полная длина слоя.
Для численного решения уравнений (1)-(3) использовали неявный метод Эйлера с постоянным шагом по длине и по времени. Температура на входе в слой зернистого материала Тin в общем случае не равна температуре на входе в установку, так как подводящие воздух коммуникации обладают тепловой инерционностью, поэтому Тin находили из уравнения:
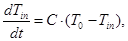(4)
В уравнении (4) коэффициент С зависит от таких параметров, как скорость фильтрации, теплоемкость воздуха и подводящих коммуникаций. Значение С рассчитывали для каждого расхода, исходя из экспериментальных данных по изменению во времени температуры воздуха на входе в установку при прямом и обратном направлении течения [8]. Для вычисления числа Nu использовали зависимость Тимофеева [9] для диапазона Re > 20.
|
|
|
|
Рис. 1. Зависимость времени переключения по первой методике от числа Re для различных засыпок при DТТ = 2.5 оС. |
Рис. 2. Зависимость времени переключения по второй методике от числа Re для свинцовых шаров D = 2.0 мм при различных DT. |
На Рис. 2 - 4 представлены результаты расчета времени полуцикла в зависимости от числа Re для шаров различного диаметра при различных DT и проведено его сравнение с опытными данными. Из рисунков видно, что наблюдается удовлетворительное совпадение времен при больших значениях чисел Re и больших DТ. При малых значениях Re заметно сказывается влияние подвода теплоты из окружающего пространства, который не учитывается уравнениями (1)-(3). В результате дополнительного подвода теплоты экспериментальные значения времени полуцикла оказываются меньше расчетных.
|
|
|
|
Рис. 3. Зависимость времени полуцикла от числа Re для свинцовых шаров D = 4.5 мм при различных DT. |
Рис. 4. Зависимость времени полуцикла от числа Re для стеклянных шаров D = 3.2 мм при различных DT.
|
4. Заключение
Представлены результаты экспериментального исследования нестационарного теплообмена при циклической фильтрации потока воздуха через зернистый слой, в качестве которого использовали свинцовые (D = 2.0, 3.5 и 4.5 мм) и стеклянные шары (D = 3.2 мм). Для исследованных засыпок измерена зависимость времени переключения направления потока воздуха от числа Рейнольдса. Разработана математическая модель процесса, описывающая теплообмен между газовым потоком и неподвижным слоем шаров. Хорошее согласование экспериментальных данных с расчетными наблюдается при больших числах Рейнольдса, в то время как при малых сказывается влияние тепловых потерь, в результате чего экспериментальное время оказывается меньше расчетного. Полученные результаты могут быть использованы при разработке регенеративных тепло- массообменных устройств.
Благодарность
Работа выполнена при финансовой поддержке молодых российских ученых и ведущих научных школ (грант МК-50.2009.8 и грант № НШ-8888.2010.8).
Литература:
1. Матрос Ю.Ш. // Кинетика и Катализ, 1981, Т. 22, № 2, С. 219-226.
2. Франк-Каменецкий Д.А. Диффузия и теплопередача в химической кинетике. М.: Наука, 1967. с. 426.
3. Боресков Г.К., Матрос Ю.Ш., Киселев О.В., Бунимович Г.А. // Докл. АН СССР, 1977, Т. 237, № 1, С. 160-163.
4. Боресков Г.К., Бунимович Г.А., Матрос Ю.Ш., Иванов А.А. // Кинетика и катализ, 1982, Т. 23, № 2, С. 402-406.
5. Аристов Ю.И., Мезенцев И.В., Мухин В.А. // ИФЖ. 2006, Т. 79, № 3. С. 151-157.
6. Аристов Ю.И., Мезенцев И.В., Мухин В.А // ИФЖ. 2006, Т. 79, № 3. С. 143-150.
7. Schuman T.E.W. Heat transfer a liquid flowing trough a porous prism // J. Franklin Inst, 1929. Vol. 208, No. 3. P. 405-416.
8. Мезенцев И.В., Верниковская Н.В., Аристов Ю.И., Мухин В.А. // Теплофизика и аэромеханика, 2006, Т. 13, № 3.
9. Тимофеев В. Н. Теплообмен в слое. В кн.: Известия ВТИ им. Ф. Э. Дзержинского, 1949, № 7, С. 12.
