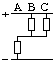К пониманию векторной системы широтно-импульсной модуляции инвертора напряжения



Одной из блестящих работ по векторным системам широтно-импульсной модуляции (ШИМ) инвертора напряжения, на наш взгляд, является работа [1]. Но рекомендовать ее студентам, начинающим овладевать данной темой, было бы преждевременно в силу высокой степени обобщения. В этой статье на конкретных примерах мы попытались пояснить смысл одной из формул в векторной форме, приведенной в [1].

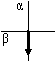
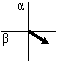
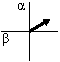
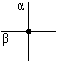
Возможные дискретные включения силовых ключей автономного инвертора напряжения (АИН) (8 различных положений) с их кодами состояния и направлением образующих векторов приводим из этой работы [1], как показано на рис. 1 и в таблице 1.

Рис. 1. Структура системы «АИН ШИМ - нагрузка»

Таблица 1

Номер комбина­ции	Состояния схемы
	1	2	3	4	5	6	7	8
Замыкание ключей	1А 2В 2С	1А 1В 2С	2А 1В 2С	2А 1В 1С	2А 2В 1С	1А 2В 1С	1А 1В 1С	2А 2В 2С
Код состояния	100	110	010	011	001	101	111	000
Схема питания нагрузки
Вектор напряже­ний

Автором [1] показывается сложность получения вращающегося вектора напряжения в любой момент времени. Максимально приближаясь к обозначениям автора фундаментальной работы, нам необходимо понять, как из ограниченного числа возможных включений силовых ключей можно получить вектор в любом положении отличных от образующих векторов (,, …, ) (рис. 2.)

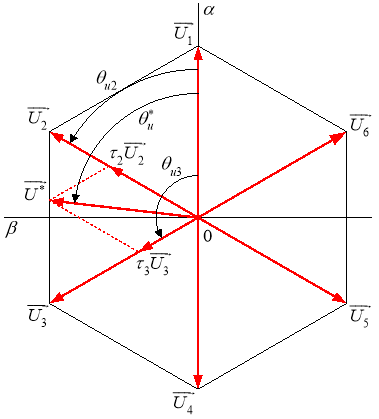
Рис. 2. Правильный шестиугольник с образующими векторами

На наш взгляд, автором неслучайно выбран промежуточный вектор , расположенный между образующими и , причем меньше образующих. Для начинающих овладевать векторной системой ШИМ наилучшим входом в понимание вращающегося вектора, наверное, является именно расположение между указанными векторами и .

Он показывает, что вращающийся вектор можно определить с помощью следующей формулы:

Именно здесь, на наш взгляд, начинающему трудно включиться в процесс понимания без конкретных примеров.

В приведенной формуле и - относительные длительности попеременного включения силовых ключей, реализующих векторы и .

Естественно, если предположить, что , т.е. за некоторый промежуток времени, равный половине периода модуляции, нагрузка будет питаться схемой с кодом 010, а другую половину - с кодом 110, то вектор будет находиться посередине векторов и .

Период, в течение которого происходят эти переключения с выдержками времени и , автор назвал периодом модуляции ШИМ или усреднения (аппроксимации).

Покажем на конкретных примерах процесс движения вектора от к (рис. 3), который является частью правильного шестиугольника. Для ускорения в процесс понимания примем модули образующих векторов за единицу, т.е. . Когда будет понят весь механизм движения вектора , можно сделать привязку к напряжению выпрямителя . Длину векторов и полезно взять 10 см, тогда проще проконтролировать полученные результаты на калькуляторе или на компьютере.

Построим декартову систему координат. Горизонтальную ось (+j) обозначим β, вертикальную (+1) – α.

Соединим вершины векторов и прямой, перпендикулярной оси β. Для более корректного построения проведем дугу окружности от к и разделим на десять частей (за один период напряжения сети уложится шестьдесят периодов модуляции или при частоте 50 Гц частота модуляций составит 3 кГц). Соединим их с началом координат. Обозначим точки пересечения с прямой : 1, 2, 3, …, 10.

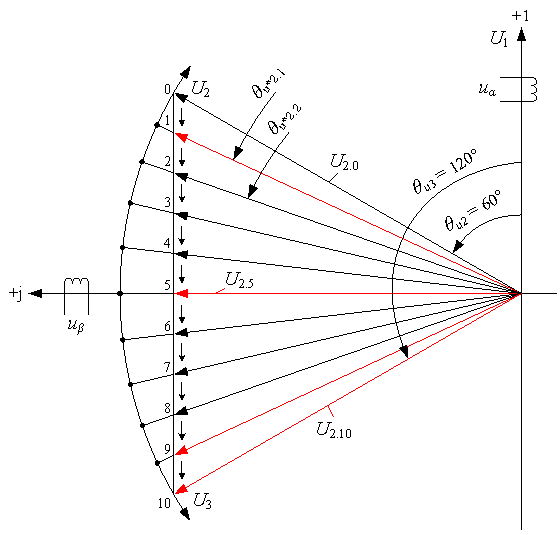
Рис. 3. Последовательный переход вращающегося вектора от образующего вектора к по вертикальной линии

Покажем векторы , , , …, и рассмотрим работу формулы при движении от к по вертикали за соответствующие периоды модуляции (аппроксимации или усреднения).

Длительности и заданы следующим образом (модуль ) [1]:

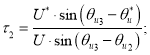
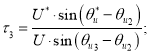
В конце работы в примечании дадим выводы формулы для τ₂.

1. Движение вращающегося вектора по вертикальной линии шестиугольника (рис. 3).

Подробно дадим расчет для точек 1, 5, 9 и 10. Результаты расчетов остальных точек сведем в общую таблицу 2.

Точка 1 (рис. 3).

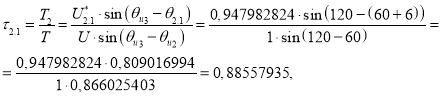
где или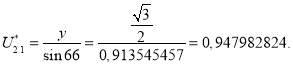

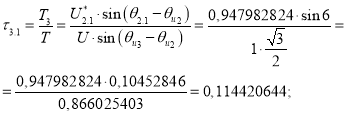
Так как , следовательно, (рассматриваем идеализированные ключи, не учитываем «мертвое время»).

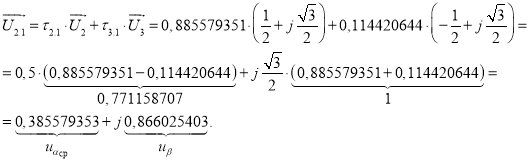
К моменту времени τ (период T) вектор повернулся против часовой стрелки на 6°, и его модуль уменьшился до 0,947982825 вследствие попеременного переключения силовых ключей с кодами 010 → 110 → 010.

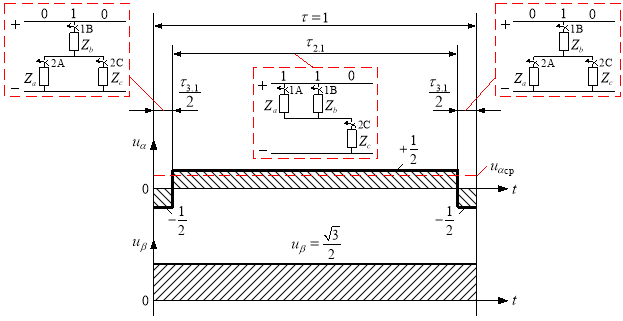
Рис. 4. Картина процесса получения среднего вектора

Точка 5 (рис. 3).

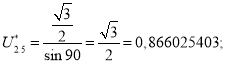
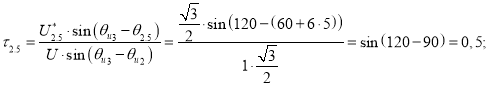
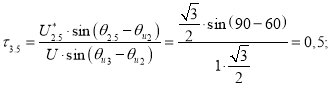
Так как , то (рис. 5).

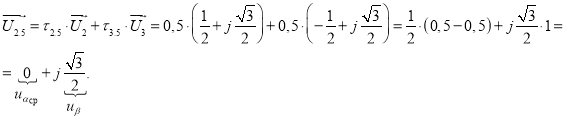
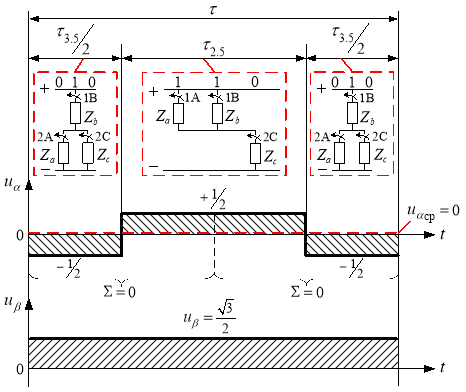
Рис. 5. Картина процесса получения среднего вектора

Точка 9 (рис. 3).

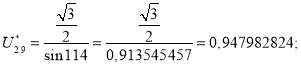
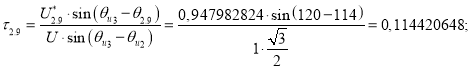
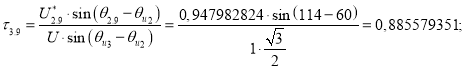
Так как , то (рис. 6).

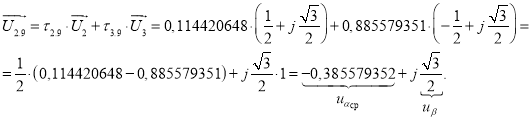
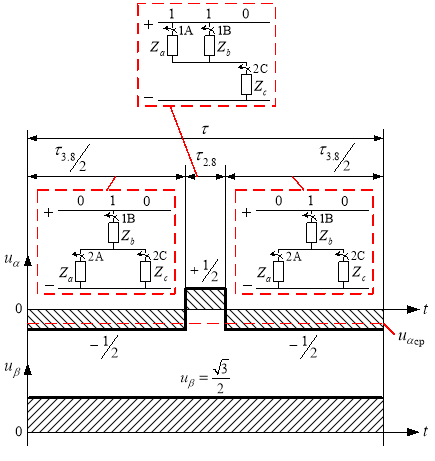
Рис. 6. Картина процесса получения среднего вектора

Точка 10 (рис. 3).

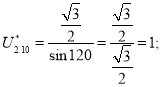
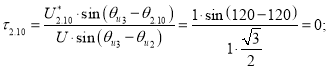
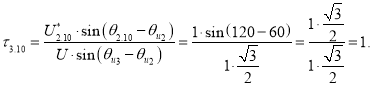
Так как , то .

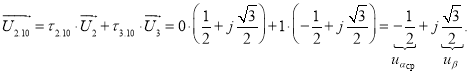
Таблица 2

№
1	0,947982824	0,885579351	0,114420644	1	0	0,385579353	0,866025403
2	0,910593	0,781388714	0,218611289	1	0	0,281388712	0,866025403
3	0,885372925	0,684079381	0,315920617	1	0	0,184079382	0,866025403
4	0,870795713	0,591022937	0,408977062	1	0	0,091022937	0,866025403
5	0,866025403	0,5	0,5	1	0	0	0,866025403
6	0,870795713	0,408977062	0,591022937	1	0	-0,091022937	0,866025403
7	0,885372925	0,315920617	0,684079381	1	0	-0,184079382	0,866025403
8	0,910593	0,218611289	0,89169054	1	0	-0,33653977	0,866025403
9	0,947982824	0,114420648	0,885579351	1	0	-0,385686435	0,866025403
10	1	0	1	1	0	-0,5	0,866025403

2. Движение вращающегося вектора по дуге с радиусом (рис. 7).

Приведем расчет для точек 2’, 9’ и 10’. Результаты расчетов остальных точек сведем в общую таблицу 3.

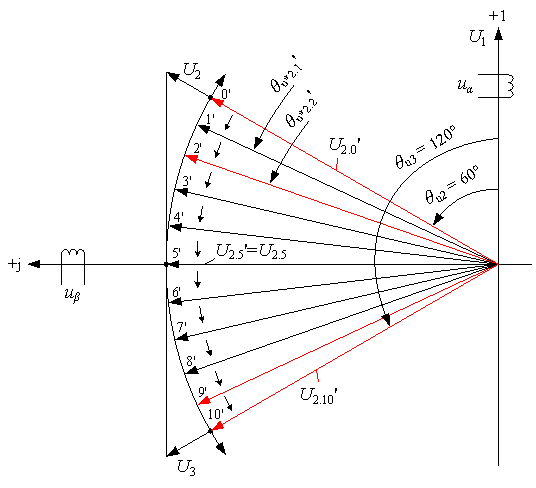
Рис. 7. Последовательный переход вращающегося вектора от образующего вектора к по дуге с радиусом

Точка 2’ (рис. 7).

Модуль

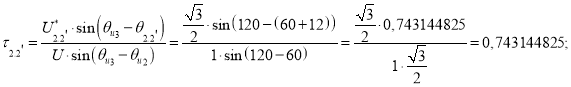
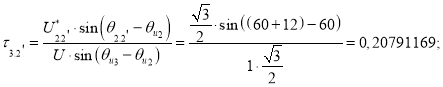
Таким образом, для того, чтобы уменьшить модуль вектора с 0,910593 для точки (2) до , необходимо сделать паузу с общим временем отключения (рис. 8).

Получим среднее напряжение за период модуляции:

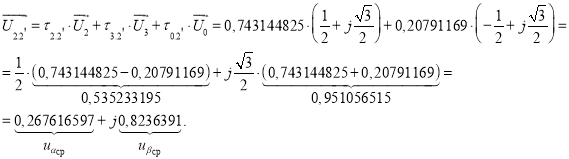
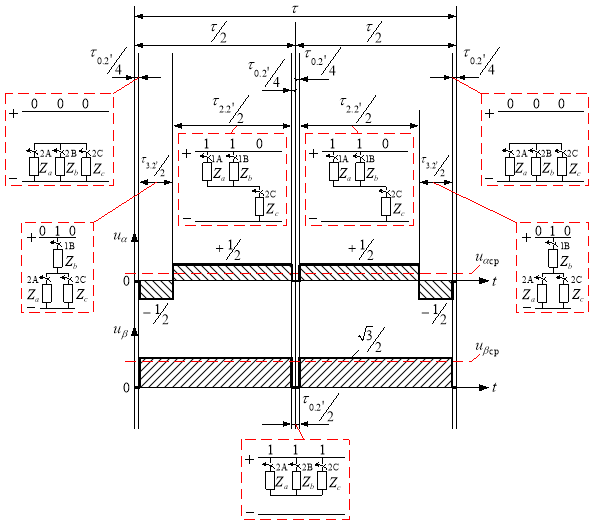
Рис. 8. Картина процесса получения среднего вектора

Точка 9’ (рис. 7).

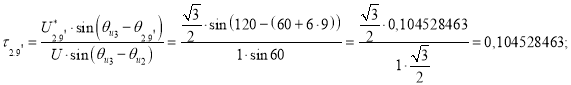
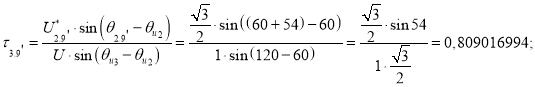
Определим среднее напряжение за период модуляции (рис. 9):

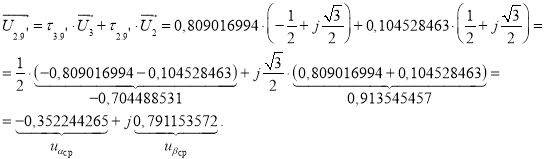
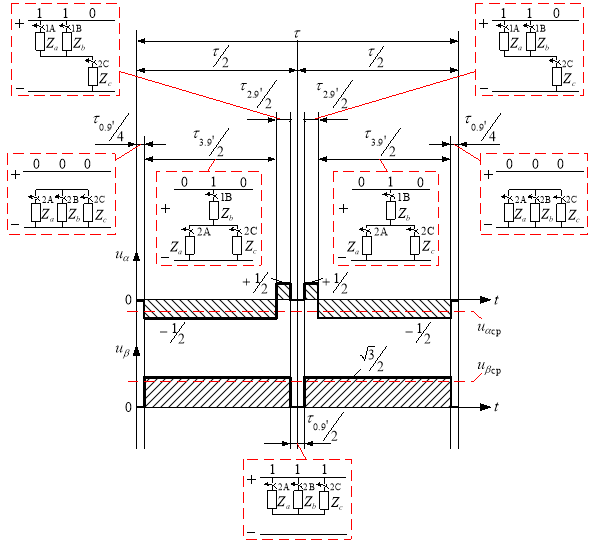
Рис. 9. Картина процесса получения среднего вектора

Точка 10’ (рис. 7).

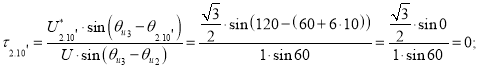
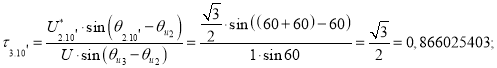
Определим среднее напряжение за период аппроксимации:

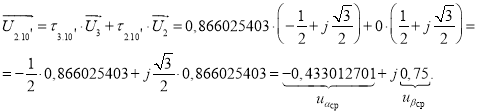
Таблица 3

№
1	0,866025403	0,809017	0,104528463	0,91354563	0,086454536	0,351866185	0,791153573
2	0,866025403	0,743144825	0,20791169	0,951056515	0,048943484	0,267616597	0,8236391
3	0,866025403	0,669130606	0,309017	0,9781476	0,0218524	0,360113606	0,9781476
4	0,866025403	0,587785252	0,406736643	0,994521895	0,005478105	0,090524304	0,861281224
5	0,866025403	0,5	0,5	1	0	0	0,866025403
6	0,866025403	0,406736643	0,587785252	0,994521895	0,005478105	-0,090524304	0,861281224
7	0,866025403	0,309016994	0,669130606	0,9781476	0,021852399	-0,180056806	0,847100669
8	0,866025403	0,20791169	0,743144825	0,951056515	0,048943484	-0,267616462	0,823639101
9	0,866025403	0,104528463	0,809016994	0,913545457	0,086454543	-0,352244265	0,791153572
10	0,866025403	0	0,866025403	0,866025403	0,133974597	-0,433012701	0,75

Примечание:

К выводу формул определения относительной длительности τ₂

Ранее была приведена следующая формула для определения :

Рассмотрим это уравнение для точки 4 (рис. 10). Для этой точки τ₀ = 0, поэтому:

Через проекции:

Для точки 4 τ_2.4 = 0,6; τ_3.4 = 0,4.

Примем U₂ = U₃ = 1, тогда

Вектор совпадает с ранее полученным другим путем.

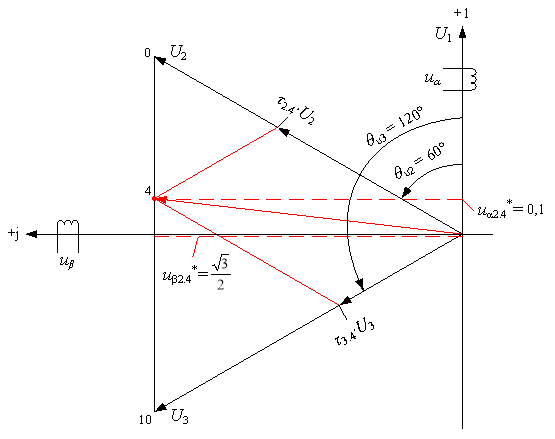
Рис. 10. К пояснению формулы

К выводу относительной длительности включения ключей τ₂

В соответствии с рис. 2 проекции модуля вектора на оси α и β определятся по следующим формулам:

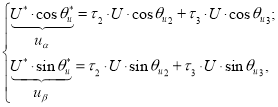
где

Умножим первое уравнение на , а второе на :

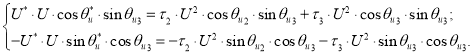
Сложим полученные уравнения и разделим на U:

Выразим τ₂:

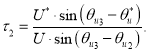
Вывод формулы для относительной длительности τ₃ производится аналогично.

Возвращаясь к формуле , с которой мы начали, к сожалению, необходимо отметить, что сделан нами только первый шаг к ее пониманию на конкретных примерах. В конечном счете наиболее глубокое понимание смысла придет только после ее реализации в системе управления АИН ШИМ на микроконтроллере.

Литература:

1. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. - Екатеринбург: УРО РАН, 2000. - 654 с.