Адаптивное воспроизведение мультисинусоидального сигнала в системе с запаздыванием по входу
Автор: Милюшин Александр Сергеевич
Рубрика: 3. Автоматика и вычислительная техника
Опубликовано в
Дата публикации: 17.06.2017
Статья просмотрена: 102 раза
Библиографическое описание:
Милюшин, А. С. Адаптивное воспроизведение мультисинусоидального сигнала в системе с запаздыванием по входу / А. С. Милюшин. — Текст : непосредственный // Технические науки: проблемы и перспективы : материалы V Междунар. науч. конф. (г. Санкт-Петербург, июль 2017 г.). — Санкт-Петербург : Свое издательство, 2017. — С. 37-40. — URL: https://moluch.ru/conf/tech/archive/231/12635/ (дата обращения: 26.04.2024).
Данная работа посвящена решению задачи синтеза алгоритма адаптивного управления системами с запаздыванием по входу, дается описание существующего неадаптивного решения для таких систем, предлагается адаптивный алгоритм с использованием фильтрации, полученный результат может представлять интерес для различных отраслей автоматики и робототехники.
Ключевые слова: адаптивное управление, системы с запаздыванием, алгоритм адаптивного управления
Технические системы с запаздыванием широко распространены в реальной жизни, причем описать их с помощью математических моделей без учета запаздывания удается далеко не всегда, поскольку такое описание не редко не обеспечивает необходимую точность. Также важное значение для современной промышленности может иметь решение задачи адаптивного воспроизведения неизвестных мультисинусоидальных сигналов [7]. Данные методы могут быть востребованы, например, для робототехнических систем в которых применяется следование по траектории (в данном случае траектория может быть рассмотрена как совокупность участков, каждый из которых может быть описан с помощью наперед неизвестного мультисинусоидального сигнала).
Постановка задачи.
Рассмотрим систему, описываемую следующей системой уравнений:
![]() (1)
(1)
где x –вектор состояния объекта, y — вектор выхода объекта системы, A — матрица состояния объекта, b — матрица управления объекта, C — матрица выхода, причем A, b и C –известны, матрица A к тому же устойчива. ![]() — сигнал управления, где t — текущее время,
— сигнал управления, где t — текущее время, ![]() - запаздывание.
- запаздывание.
Целью является построение алгоритма управления, который обеспечит соблюдение следующего равенства (2):
![]() (2)
(2)
где g — ограниченный сигнал задающего мультисинусоидального воздействия генерируемый следующей системой (3):
![]() (3)
(3)
где Г и H известные матрицы состояния и выхода системы генерации мультисинусоидального сигнала, z — вектор состояний этой системы.
Математическая модель системы.
Для нахождения матрицы Г используется метод последовательного дифференцирования функции [1, 2]. Приведем конкретный пример. Предположим необходимо получить модель следующего сигнала: ![]() . Примем за первую координату
. Примем за первую координату ![]() саму исходную функцию, а последующие координаты будут представлять из себя последовательные производные этой функции:
саму исходную функцию, а последующие координаты будут представлять из себя последовательные производные этой функции:
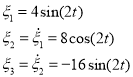 (3)
(3)
Можно видеть, что ![]() может быть выражена через
может быть выражена через ![]() :
: ![]() , принимая во внимание также, что
, принимая во внимание также, что ![]() получим:
получим:
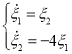 (4)
(4)
Учитывая (3) и приняв вектор ![]() можно записать полученный результат в матричной форме (5):
можно записать полученный результат в матричной форме (5):
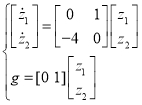 (5)
(5)
Таким образом был построен генератор синусоидального воздействия. В дальнейшем в статье представлены решения следующих задач:
- Построение неадаптивного алгоритма управления для системы без запаздывания.
- Построение неадаптивного алгоритма управления для системы с запаздыванием.
- Построение адаптивного алгоритма управления с компенсацией запаздывания.
Решения первых трех задач служат вспомогательным целям и достаточно широко освещены как в отечественной так и зарубежной литературе.
- Построение неадаптивного алгоритма управления для системы без запаздывания
Система управления и объект управления описываются следующим образом:
![]() (6)
(6)
Генератор синусоидального воздействия описывается в соответствии с (3).
Для данного примера были выбраны следующие значения параметров системы:
![]() (7)
(7)
Для генерации синусоидального сигнала воспользуемся примером (5). Из теории автоматического управления известен следующий закон управления [4, 5]:
![]() (8)
(8)
где K — матрица линейных стационарных обратных связей, Lg – матрица обратных связей по выходу эталонной модели. Поскольку матрица А устойчива, то элементы вектора K можно принять равными нулю. Расчет элементов вектора Lg осуществляется через решение следующей системы матричных уравнений [3]:
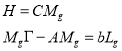 (9)
(9)
где матрица Mg — матрица согласования размерностей объекта управления и эталонной модели.
В итоге было получено значение Lg = [-8 -3]. В результате моделирования в прикладном пакете Simulink были получены следующие результаты (рис. 1):
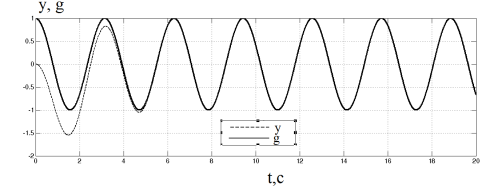
Рис. 1. Результаты моделирования для неадаптивного регулятора слежения
Как видно из графика выход системы сходится к эталонному сигналу, за ограниченный промежуток времени.
- Построение неадаптивного алгоритма управления для системы сзапаздыванием.
Система описывается уравнениями вида (1), было принято равным 7 с. Все остальные значения идентичны значениям предыдущего раздела. Для решения задачи был предложен следующий алгоритм управления [1]:
![]() (10)
(10)
Учитывая устойчивость матрицы А первое слагаемое правой части обнуляется. В результате моделирования в прикладном программном пакете Simulink были получены результаты, представленные на рисунке 2.
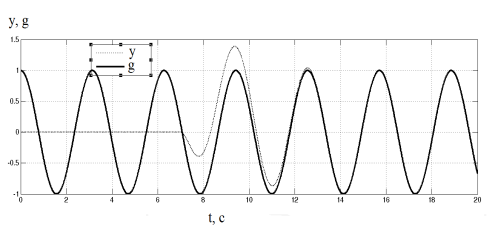
Рис. 2. Результаты моделирования для неадаптивного алгоритма управления системы с запаздыванием в канале управления
Как видно из графика на рисунке 2 выходной сигнал системы сходится к сигналу эталонной модели, при этом реагирование начинается после того, как проходит период запаздывания — в нашем случае 7 секунд.
- Построение адаптивного регулятора для системы сзапаздыванием.
Все значения показателей приняты как в предыдущих пунктах, генератор задающего сигнала задан следующей системой:
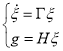 (11)
(11)
где — вектор состояний эталонной модели. Матрицы Г и Н как в (3).
Основная идея заключается в применение фильтрации в алгоритме адаптации [6]. Фильтр представлен передаточной функцией, рассчитываемой по формуле (12):
![]() (12)
(12)
где s — оператор дифференцирования.
Для нашего случая фильтр будет иметь вид: ![]() . Был найден следующий закон управления:
. Был найден следующий закон управления:
![]() (13)
(13)
![]() генерируется следующим алгоритмом адаптации с использованием фильтрации:
генерируется следующим алгоритмом адаптации с использованием фильтрации:
![]() (14)
(14)
где γ — некоторый положительный коэффициент, в общем случае влияющий на скорость сходимости, в нашем эксперименте взято значение γ = 100, ξ(t — ) — вектор состояния эталонной системы с учетом запаздывания, ![]() — разница между оценкой отклонения выходного сигнала объекта управления от сигнала задания
— разница между оценкой отклонения выходного сигнала объекта управления от сигнала задания ![]() и его реальным значением
и его реальным значением ![]() . Расчет оценки осуществляется также с применением фильтра (15):
. Расчет оценки осуществляется также с применением фильтра (15):
![]() (15)
(15)
где вектор
В результате проведенного в Simulink моделирования были получены результаты, представленные на рисунках 3, 4.
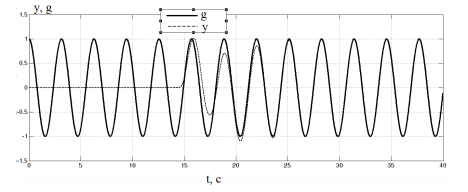
Рис. 3. Результаты моделирования адаптивного регулятора с запаздыванием (выход объекта управления y и генератора задания сигнала g)
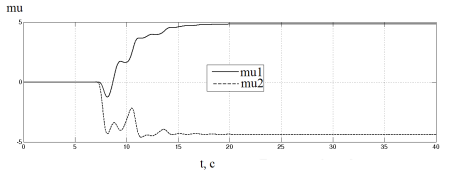
Рис. 4. Результаты моделирования адаптивного регулятора с запаздыванием (элементы вектора ![]() )
)
На графиках показано, что выходной сигнал объекта управления сходится к сигналу генератора синусоидального сигнала, а элементы вектора ![]() принимают ограниченные значения.
принимают ограниченные значения.
Выводы.
В статье представлен алгоритм адаптации для управления объектом управления с учетом запаздывания по входу. Моделирование показало, что алгоритм обеспечивает сходимость выходного сигнала объекта к задающему сигналу, а также ограниченность внутренних сигналов алгоритма.
Литература:
- Бобцов А. А., Никифоров В. О., Пыркин А. А., Адаптивное управление возмущенными системами. Учебное пособие СПб.: Университет ИТМО, 2015. — 126 с.
- Бобцов А. А., Пыркин А. А. Адаптивное и робастное управление с компенсацией неопределенностей. Учебное пособие. — СПб.: НИУ ИТМО, 2013. — 135 с.
- Герасимов Д. Н., Никифоров В. О., Адаптивное и робастное управление линейными динамическими системами. — СПб: Университет ИТМО, 2015. — 93 с.
- Григорьев В. В., Журавлёва Н. В., Лукьянова Г. В., и др. Синтез систем автоматического управления методом модального управления. — С-Пб: СПбГУ ИТМО, 2007. — 108 с.
- Григорьев В. В., Лукьянова Г. Современная теория систем управления. СПбГУ ИТМО. — 2010.
- Gerasimov D., Nikiforov V. Simple Adaptive Output Control of Linear Systems // Proc. Multi-Conference on Systems and Control. 2014. P. 566–571.
- Pyrkin A., Bobtsov A., Nikiforov V. and Aranovskiy S. Output Adaptive Controller for Linear System with Input Delay and Multisinusoidal Disturbance. IEEE Conferenceon Control Applications (CCA) Part of 2014 IEEE Multi-conference on Systems and Control October 8–10, 2014. Antibes, France. pp. 1777–1782.
Ключевые слова
адаптивное управление, системы с запаздыванием, алгоритм адаптивного управленияПохожие статьи
Применение адаптивных фильтров для анализа сигналов
результат моделирования, система, эталонная модель, неадаптивный алгоритм управления, учет запаздывания, алгоритм адаптации, выходной сигнал, адаптивный регулятор, адаптивное управление...
Технологические объекты второго порядка с запаздыванием
Ключевые слова: адаптивное управление, системы с запаздыванием, алгоритм адаптивного управления. Построение неадаптивного алгоритма управления для системы без запаздывания. Система управления и объект управления описываются следующим образом.
Метод синтеза гибридных систем адаптации | Статья в журнале...
Требуется построить адаптивную систему управления таким образом, чтобы при любом наборе , при любых начальных
Результаты имитационного моделирования показывают, что большинство, построенных с помощью данного метода, систем управления обладают...
Модель адаптивной системы управления и ее применение для...
Введение. В последнее время постоянно увеличивается число задач, для решения которых оказывается целесообразно или необходимо использовать автономные адаптивные системы управления.
Способы построения гибридных систем управления
Ключевые слова:прямое адаптивное управление, гибридные системы управления. Характерная особенность гибридных систем управления (ГСУ) заключается в том, что объект управления в них функционирует во времени непрерывно, а измерение выходных координат...
Алгоритмы настройки для гибридной системы управления...
В условиях априорной неопределенности задачу синтеза гибридной адаптивной системы управления (ГАСУ) с явной эталонной моделью для линейного объекта с запаздыванием по состоянию можно решить в рамках критерия гиперустойчивости [1, 2, 10]...
Моделирование систем с использованием блока чистого...
При моделировании систем управления в пакете Simulink, как правило, используется блок чистого запаздывания, так как большинство реальных объектов обладает этим запаздыванием. Пример такой модели приведен на рисунке 1.
Поиск допустимого управления в задаче стабилизации
Ключевые слова: адаптивное управление, системы с запаздыванием, алгоритм адаптивного управления.
Синтез регулятора системы управления электроприводами...
Построение неадаптивного алгоритма управления для системы...
Похожие статьи
Применение адаптивных фильтров для анализа сигналов
результат моделирования, система, эталонная модель, неадаптивный алгоритм управления, учет запаздывания, алгоритм адаптации, выходной сигнал, адаптивный регулятор, адаптивное управление...
Технологические объекты второго порядка с запаздыванием
Ключевые слова: адаптивное управление, системы с запаздыванием, алгоритм адаптивного управления. Построение неадаптивного алгоритма управления для системы без запаздывания. Система управления и объект управления описываются следующим образом.
Метод синтеза гибридных систем адаптации | Статья в журнале...
Требуется построить адаптивную систему управления таким образом, чтобы при любом наборе , при любых начальных
Результаты имитационного моделирования показывают, что большинство, построенных с помощью данного метода, систем управления обладают...
Модель адаптивной системы управления и ее применение для...
Введение. В последнее время постоянно увеличивается число задач, для решения которых оказывается целесообразно или необходимо использовать автономные адаптивные системы управления.
Способы построения гибридных систем управления
Ключевые слова:прямое адаптивное управление, гибридные системы управления. Характерная особенность гибридных систем управления (ГСУ) заключается в том, что объект управления в них функционирует во времени непрерывно, а измерение выходных координат...
Алгоритмы настройки для гибридной системы управления...
В условиях априорной неопределенности задачу синтеза гибридной адаптивной системы управления (ГАСУ) с явной эталонной моделью для линейного объекта с запаздыванием по состоянию можно решить в рамках критерия гиперустойчивости [1, 2, 10]...
Моделирование систем с использованием блока чистого...
При моделировании систем управления в пакете Simulink, как правило, используется блок чистого запаздывания, так как большинство реальных объектов обладает этим запаздыванием. Пример такой модели приведен на рисунке 1.
Поиск допустимого управления в задаче стабилизации
Ключевые слова: адаптивное управление, системы с запаздыванием, алгоритм адаптивного управления.
Синтез регулятора системы управления электроприводами...
Построение неадаптивного алгоритма управления для системы...











