Статья посвящена цифровым адаптивным фильтрам, параметры которых автоматически подстраиваются под статистические свойства обрабатываемого сигнала. Это позволяет создавать системы обработки сигналов, успешно функционирующие в присутствии помех. Рассмотрим сигнал, представляющий собой сумму гармонических составляющих с неизвестными амплитудами и фазами. Задан набор частот возможных гармонических составляющих. Требуется определить:
1. Наличие определенной составляющей в исходном сигнале;
2. При наличии составляющей — определить ее амплитуду и начальную фазу.
Для решения задачи предлагается использовать адаптивные фильтры.
Пусть входной дискретный случайный сигнал 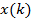 обрабатывается нерекурсивным дискретным фильтром порядка
обрабатывается нерекурсивным дискретным фильтром порядка 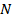 , коэффициенты которого представлены вектор‑столбцом
, коэффициенты которого представлены вектор‑столбцом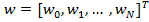 . Выходной сигнал фильтра равен:
. Выходной сигнал фильтра равен:
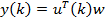 ,
,
где 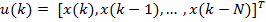 — вектор-столбец отсчетов входного сигнала. Также есть образцовый сигнал
— вектор-столбец отсчетов входного сигнала. Также есть образцовый сигнал 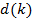 . Ошибка воспроизведения образцового сигнала — разница между образцовым сигналом
. Ошибка воспроизведения образцового сигнала — разница между образцовым сигналом 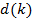 и выходом фильтра
и выходом фильтра 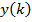 с коэффициентами
с коэффициентами 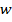 равна:
равна:
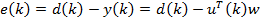 . [1, c. 47]
. [1, c. 47]
Необходимо найти такие коэффициенты фильтра 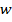 , которые обеспечивают максимальную близость выходного сигнала фильтра к образцовому, то есть минимизируют ошибку
, которые обеспечивают максимальную близость выходного сигнала фильтра к образцовому, то есть минимизируют ошибку 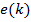 . Так как
. Так как 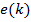 является случайным процессом, в качестве меры ее величины принимается средний квадрат. Соответственно, целевая функция выглядит так:
является случайным процессом, в качестве меры ее величины принимается средний квадрат. Соответственно, целевая функция выглядит так:
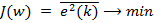 . [1, c. 60]
. [1, c. 60]
Квадрат ошибки равен:
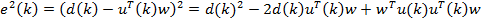
Статистически усредняя это выражение, получаем следующее:
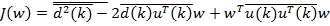 .
.
Входящие в полученную формулу усредненные величины имеют следующий смысл:
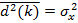 – средний квадрат образцового сигнала;
– средний квадрат образцового сигнала;
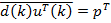 – транспонированный вектор-столбец
– транспонированный вектор-столбец 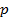 взаимных корреляций между
взаимных корреляций между 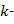 м отсчетом образцового сигнала и содержимым линии задержки фильтра (входным сигналом);
м отсчетом образцового сигнала и содержимым линии задержки фильтра (входным сигналом);
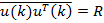 — корреляционная матрица сигнала размера
— корреляционная матрица сигнала размера 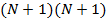 . Для стационарного случайного процесса корреляционная матрица имеет вид матрицы Теплица, то есть на ее диагоналях стоят одинаковые величины [3, c. 280]:
. Для стационарного случайного процесса корреляционная матрица имеет вид матрицы Теплица, то есть на ее диагоналях стоят одинаковые величины [3, c. 280]:
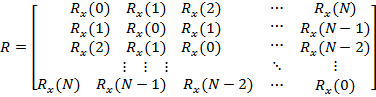 ,
,
где 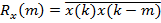 — корреляционная функция случайного процесса
— корреляционная функция случайного процесса 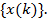
С учетом введенных обозначений целевая функция принимает следующий вид:
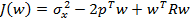 .
.
Данное выражение представляет собой квадратичную форму относительно 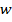 и потому при невырожденной матрице
и потому при невырожденной матрице 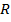 имеет единственный минимум, для нахождения которого необходимо приравнять нулю вектор градиента:
имеет единственный минимум, для нахождения которого необходимо приравнять нулю вектор градиента:
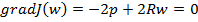 .
.
Отсюда получаем искомое решение для оптимальных коэффициентов фильтра:
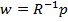 .
.
Подстановка этого выражения в конечную формулу целевой функции даёт минимально достижимую дисперсию сигнала ошибки:
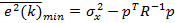 .
.
Для нахождения минимума целевой функции можно использовать метод наискорейшего спуска. При использовании данного способа оптимизации вектор коэффициентов фильтра 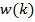 должен рекурсивно обновляться следующим образом:
должен рекурсивно обновляться следующим образом:
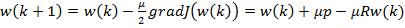 ,
,
где 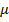 — положительный коэффициент, называемый размером шага.
— положительный коэффициент, называемый размером шага.
Алгоритм сходится, если 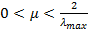 , где
, где 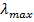 – максимальное собственное число корреляционной матрицы R. [1, c. 69] Скорость сходимости при этом зависит от разброса собственных чисел корреляционной матрицы
– максимальное собственное число корреляционной матрицы R. [1, c. 69] Скорость сходимости при этом зависит от разброса собственных чисел корреляционной матрицы 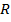 : чем меньше отношение
: чем меньше отношение 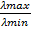 , тем быстрее сходится итерационный процесс.
, тем быстрее сходится итерационный процесс.
Однако для расчета градиента необходимо знать значения матрицы 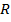 и вектора
и вектора 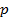 . На практике могут быть доступны лишь оценки этих значений, получаемые по входным данным. Простейшими такими оценками являются мгновенные значения корреляционной матрицы и вектора взаимных корреляций, получаемые без какого-либо усреднения:
. На практике могут быть доступны лишь оценки этих значений, получаемые по входным данным. Простейшими такими оценками являются мгновенные значения корреляционной матрицы и вектора взаимных корреляций, получаемые без какого-либо усреднения:
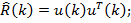
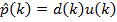 .
.
При использовании данных оценок формула вычисления 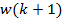 принимает следующий вид:
принимает следующий вид:
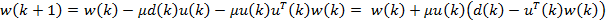 .
.
Выражение, стоящее в скобках, представляет собой разность между образцовым сигналом и выходным сигналом фильтра на k-м шаге, то есть ошибку фильтрации 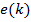 . Таким образом, выражение для рекурсивного обновления коэффициентов фильтра оказывается достаточно простым:
. Таким образом, выражение для рекурсивного обновления коэффициентов фильтра оказывается достаточно простым:
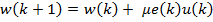 .
.
Алгоритм адаптивной фильтрации, основанный на этой формуле, получил название МНК (метод наименьших квадратов или LMS — LeastMeanSquare,).
Анализ сходимости алгоритма МНК показывает, что верхняя граница для размера шага 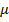 в данном случае является меньшей, чем при использовании истинных значений градиента. Эта граница примерно равна
в данном случае является меньшей, чем при использовании истинных значений градиента. Эта граница примерно равна
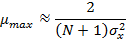
где 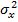 — средний квадрат входного сигнала фильтра. [2, c. 320]
— средний квадрат входного сигнала фильтра. [2, c. 320]
Исследования сигналов с использованием алгоритма МНК проводились на модели, реализованной в пакете в Matlab.
Далее приводятся результаты работы программы для фильтра 12000 порядка. Частота дискретизации анализируемого сигнала равна 6/3600=1,(6)*10–3Гц. Полоса пропускания фильтра по уровню 3 дБ составляет 2,3*10–7 Гц или 1,4*10–4 частоты дискретизации. Графики на рисунках 1–2 соответствуют двум гармоническим составляющим, одна из которых входит в полосу пропускания фильтра, а вторая не входит; сигнал на выходе адаптивного фильтра после 4000-го отсчета совпадает с тестовым. На рисунке 3 показана ошибка фильтрации в случае, когда тестовый сигнал не совпадает ни с одной частотой. Таким образом, адаптивный фильтр можно использовать для определения факта наличия или отсутствия заданной гармонической составляющей во входном сигнале.
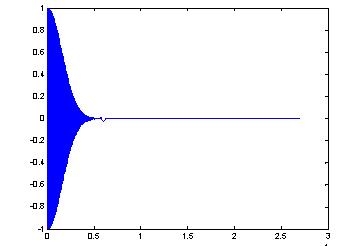
Рис. 1. Ошибка фильтрации (образцовый сигнал соответствует частоте одного сигнала)
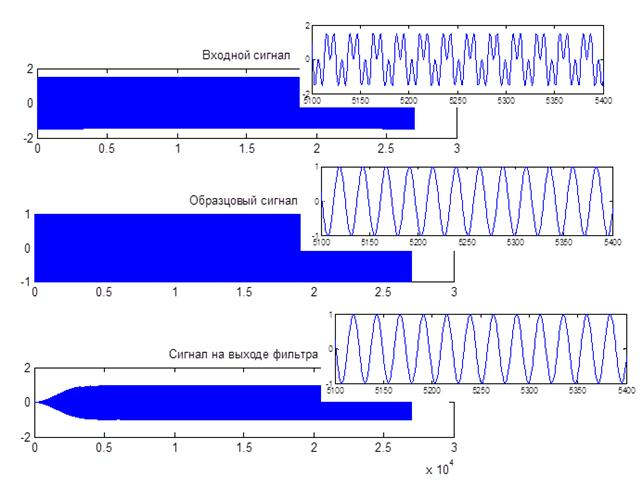
Рис. 2. Входной сигнал, образцовый сигнал и сигнал на выходе фильтра (образцовый сигнал соответствует частоте одного сигнала)
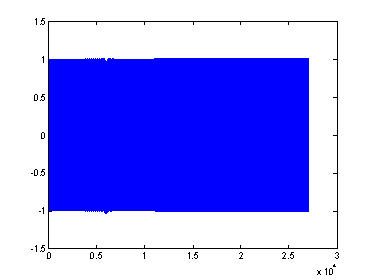
Рис. 3. Ошибка фильтрации (образцовый сигнал не соответствует частотам входного сигнала)
На рисунках 4–5 показаны ошибка фильтрации и сигналы для случая, когда оба сигнала находятся в полосе пропускания фильтра (разница частот составляет 10–7). Очевидно, что адаптивный фильтр позволяет определить наличие сигнала заданной частоты и в случае присутствия сигнала близкой частоты; при этом увеличивается время установления выходного сигнала (переходного процесса).
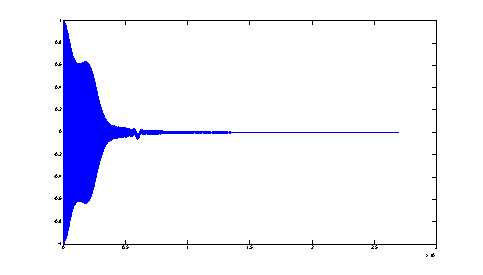
Рис. 4. Ошибка фильтрации (двухчастотный входной сигнал с частотами в полосе фильтра)
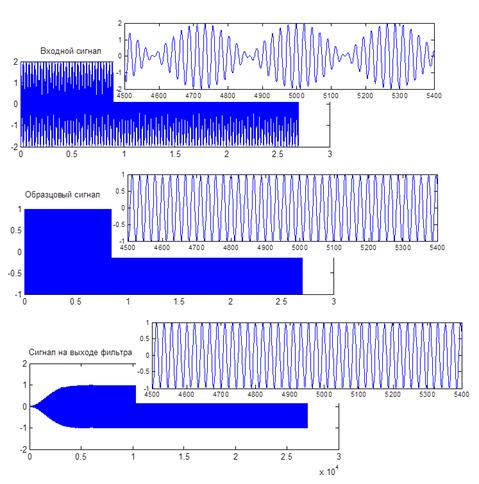
Рис. 5. Входной сигнал, образцовый сигнал и сигнал выходе фильтра (двухчастотный входной сигнал с частотами в полосе фильтра)
В рассмотренных выше экспериментах начальная фаза и амплитуда тестовых сигналов равна фазе и амплитуде образцового сигнала. При изменении начальной фазы или амплитуды тестовых сигналов выходной сигнал фильтра совпадает с тестовым, т. е. действительно выполняется минимизация ошибки выходного сигнала фильтра и образцового сигнала. Очевидно, что для определения амплитуды и начальной фазы сигнала необходимо проанализировать АЧХ и ФЧХ фильтров.
Для установления степени влияния на результаты фильтрации начальной фазы входного сигнала сравниваются частотные характеристики фильтров при подаче входного сигнала сначальной фазой, совпадающей с начальной фазой образцового сигнала, и со сдвигом фазы 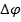 .
.
Образцовый сигнал: 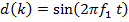 . По полученным коэффициентам фильтра для входного сигнала со сдвигом
. По полученным коэффициентам фильтра для входного сигнала со сдвигом 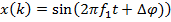 и для входного сигнала без сдвига фазы
и для входного сигнала без сдвига фазы 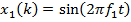 (назовем его базовым) рассчитываются частотные характеристики фильтров:
(назовем его базовым) рассчитываются частотные характеристики фильтров:
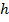 — комплексный коэффициент передачи фильтра при обработке сигнала со сдвигом фаз;
— комплексный коэффициент передачи фильтра при обработке сигнала со сдвигом фаз;
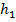 — комплексный коэффициент передачи фильтра при обработке сигнала без сдвига.
— комплексный коэффициент передачи фильтра при обработке сигнала без сдвига.
На рисунке 6 показаны ФЧХ фильтров. Видно, что ФЧХ фильтра, полученная для сигнала со сдвигом фазы, сдвинута относительно ФЧХ базового фильтра.
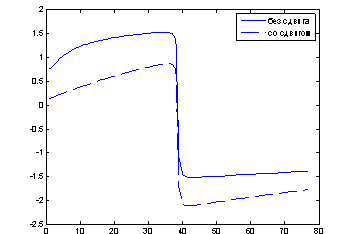
Рис. 6. Фазовые характеристики фильтра для сигнала со сдвигом фаз и без него
Сдвиг фазы сигнала можно вычислить усреднением разности ФЧХ в диапазоне определения ФЧХ: 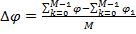 ,
,
где  .
.
Зависимость ошибки определения начальной фазы сигнала от величины сдвига показана на рисунке 7.
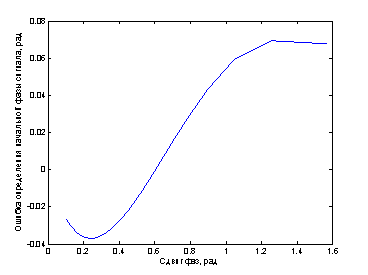
Рис. 7. Ошибка определения начальной фазы
На рисунке 8 показана зависимость ошибки определения фазы для случая суммы двух гармонических сигналов, входящих в полосу фильтра.
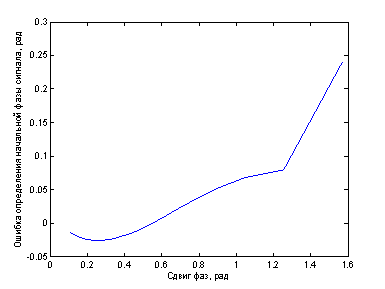
Рис. 8. Ошибка определения начальной фазы для суммы двух частот
Путем последовательной коррекции начальной фазы образцового сигнала можно точно определить начальную фазу тестируемого сигнала; нулевая ошибка соответствует сдвигу π/5.
Для определения амплитуды входного сигнала необходимо рассчитать:
- реакцию фильтра 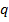 на образцовый сигнал для коэффициентов фильтра
на образцовый сигнал для коэффициентов фильтра 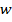 , полученных для заданного входного сигнала;
, полученных для заданного входного сигнала;
- реакцию фильтра  на образцовый сигнал для коэффициентов фильтра
на образцовый сигнал для коэффициентов фильтра 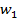 , полученных для образцового сигнала с единичной амплитудой.
, полученных для образцового сигнала с единичной амплитудой.
Тогда амплитуда сигнала 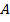 может быть определена по формуле:
может быть определена по формуле:
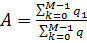 .
.
На рисунке 9 показаны графики изменения заданной амплитуды и рассчитанной амплитуды. Таким образом, можно сделать вывод о корректности описанного алгоритма расчета амплитуды сигнала и возможности определения амплитуды исследуемой гармонической составляющей с помощью адаптивного фильтра.
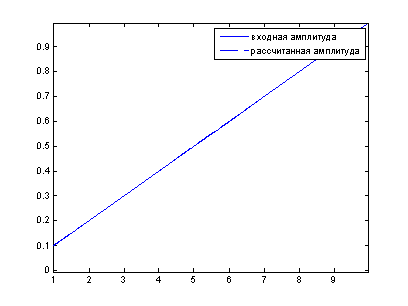
Рис. 9. Входная и рассчитанная амплитуда
Проведенные исследования показали, что адаптивные фильтры могут быть использованы для анализа параметров составляющих суммы гармонических сигналов. Сначала надо определить наличие сигнала заданной частоты в исходном сигнале. Затем определяется сдвиг начальной фазы исследуемого сигнала относительно образцового сигнала, в результате изменяется начальная фаза образцового сигнала. По модифицированному образцовому сигналу определяется амплитуда исследуемого сигнала.
Литература:
1. Адаптивные фильтры: Пер. с англ. Под ред. К.Ф. Н. Коуэна и П. М. Гранта. — М.:Мир, 1988. — 392 с.
2. Haykin S. Adaptive Filter Theory, 5th edition. / Prentice Hall, 2012. — 936 p.
3. Прокис Дж. Цифровая связь: Пер. с англ. / Под ред.Д. Д. Кловского.— М.: Радио и связь, 2000.— 800 с.







