Технологические процессы первичной переработки хлопка-сырца характеризуется значительным числом параметров, определяющих ход этих процессов, наличием внутренних связей между параметрами, их взаимным многообразным и сложным влиянием друг на друга. Для того, чтобы решить задачу создания системы оптимального управления технологическим процессом необходимо его изучить, определить степень влияния характеризующих его параметров на выходные качественные и количественные показатели процесса.
Наиболее удобным методом исследования сложных технологических процессов, позволяющим реализовать его на электронно-вычислительных машинах, отыскать оптимальные режимы ведения и условия управления процессом, является метод моделирования.
Разновидностью моделирования является построение математической модели, которая в широком плане может трактоваться как «знаковая конструкция» [1]. Для исследования и оптимизации процессов первичной переработки хлопка-сырца на основе математических методов подходит более узкое, но в то же время более определенное понимание математической модели как зависимости между параметрами процесса, полученной теоретически или экспериментально.
Математическая модель должна быть пригодна для решения поставленной задачи, адекватна процессу и учитывать физические и математические ограничения. Математическая модель исключительно компактна и удобна для исследования и управления реальными процессами первичной обработки хлопка-сырца. Во многих случаях модель позволяет также лучше понять внутреннее устройство объекта, так как при этом пользуются физическими аналогиями и математическим анализом.
Применение математической модели при экспериментально-статистическом исследовании процессов первичной обработки хлопка-сырца позволяет:
выбрать оптимальный технологический режим процесса;
сократить план исследовательских работ при разработке технологии производства;
создать систему управления процессом.
Для построения моделей технологических процессов первичной обработки хлопка-сырца можно выделить два подхода:
1) физико-механический анализ явлений» обуславливающих динамику процесса;
2) экспериментальная идентификация, при которой основную информацию о процессе получают путем непосредственных измерений.
Ввиду сложности и многообразия явлений, протекающих в процессах первичной обработки хлопка-сырца, а также в связи с большим числом составляющих их элементов, методы построения физико-химических закономерностей исследуемых технологических процессов часто оказываются малоэффективными. Это объясняется сложностью и недостаточной изученностью явлений, наблюдающихся в исследуемых процессах первичной обработки хлопка-сырца, а также плохой обозримостью получаемых результатов. Поэтому наиболее приемлемы экспериментально- статистические методы идентификации, основанные, как известно, на методах корреляционного и регрессионного анализа.
Существует много способов получения моделей технологических процессов. Каждый способ даёт возможность построить модель, адекватную процессу в том или ином смысле, что зависит от выбранного критерия. Таким образом, можно получить множество моделей изоморфных физическому объекту. Это означает, что существует некое абстрактное соответствие между множеством моделей и модулируемым объектом.
Как из множества способов выбрать тот один, или же несколько способов, которые позволяют решить поставленную задачу? Ведь при работе с конкретным технологическим объектом невозможен чисто формальный подход, приводящий к получению результатов, трудно поддающихся анализу и часто вводящих в заблуждение. Это означает, что при выборе структуры модели, критерия адекватности модели процессу и других параметров необходимо всё это увязать с целью моделирования процесса с задачей, которая стоит при разработке модели. Цели эти могут быть различными и соответственно, различными будут способы определения модели и способы её реализации.
При построении математических моделей будем считать, что основной целью является получение модели технологического процесса для управления им, хотя все исследования, связанных с определением модели и её анализом, безусловно, могут быть применены и для других задач по изучению данного процесса.
Исследуемые процессу (объекты исследования или управления) делятся на два класса. Это процессы исследованные и неисследованные.
К первому классу относятся объекты с полной информацией, для которых априори все известно. Например, при создании схем управления такими объектами известна вся информация, необходимая для управления процессом в заданном смысле, в том числе математическое описание процесса, действующие возмущения, критерий оптимальности и существующие ограничения.
Но второму классу отнесем объекты с неполной информацией, для которых такого полного значения априорной информации нет, допустим, что известно математическое описание процессов или неизвестен характер возмущений и др. Такие объекты называют «черными ящиками». Впервые термин «черный ящик» был использован для обозначения объекта, взаимосвязь между входными и выходными параметрами, которого оставалась для нас неизвестной. В работе [2] предлагается рассматривать «черный ящик» как практический метод исследования системы, недоступной для наблюдения, иногда в буквальном смысле, а иногда из-за несовершенства технических средств. В этом случае предлагается строить модель системы, такую, которая во всем существенном будет вести себя так же, как и реальная система, но в это же время будет солее доступной для экспериментирования. Таким образом, «черный ящик» является способом отображения недоступной для нас в каком-либо смысле системы. Необходимым условием отображения является то, что построенная модель должна содержать такое количество информации, которое отображало бы все разнообразие системы.
Теперь задачу разработки математических моделей оценивания параметров объектов управления можно сформулировать как задачу минимизации некоторой функции (функционала) от измеримых величин, а именно от разности выходных сигналов объекта 
и модели 
т.е.
здесь 
и 
вектор параметров объекта и модели; 
и 
обозначают векторы, транспонированные по отношению к 
; М-операция математического ожидания. Один из простых подходов может быть иллюстрирован блок-схемой, представленной на рис. 1.
Рассматривается случай выборочных измерений функций непрерывного времени. Символами
обозначены векторы соответствующих выборок, например:
Отсюда находим 
, 
где 
- постоянный шаг выборочных измерений.
.
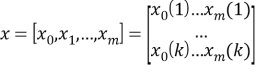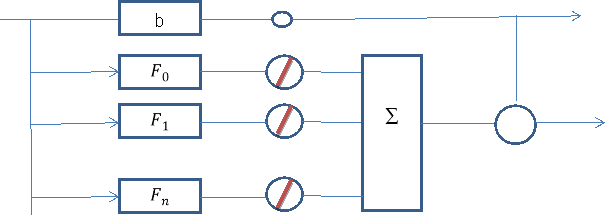
Рис. 1
Столбцы 
матрицы Х состоят из выборочных значений входных сигналов блоков 
. Эти блоки выбрани для построения требуемого описания объекта.
Теперь можно поставить задачу как отыскание оценку 
вектора параметров объекта 
по наблюдениям 
. Основываясь на имеющейся априорной информации, ниже будем рассматривать следующие методы моделирования (оценивания параметров) объектов управления [3, 4]:
1) Оценивание по методу наименьших квадратов. В этом случае не требуется никакой априорной информации и критерий определяется как
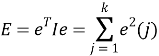, где 
Здесь I – единичная матрица. Минимизируя критерий ошибки, получаем так навиваемую систему нормальных уравнений для оценивания параметров:
Здесь, как и раньше,
означает транспонированную матрицу 
2)Марковские оценки или оценивание по обобщенному методу наименьших квадратов.
Предложим теперь, что известна ковариационная матрица аддитивного шума
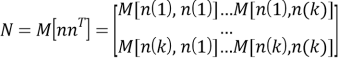
Доказано, что при 
наилучшая линейная оценка получается минимизацией выражения 
что приводит к следующему правилу оценивания:
3)Оценивание методом максимального правдоподобия. Рассмотрим вектор . Априори (до измерений) известно, что выборочные значения 
является случайными величинами с совместным распределением вероятностей
(1)
зависящим от вектора параметров . Апостериори (после измерений) становятся известными реализации этих случайных величин:
По ним определим оценку, функциональная связь между
определяется формулой (1). Для того, чтобы подчеркнуть, что формуле (1) связывает реализацию выборочных значений с вектором оценок параметров , перепишем её в виде
.
Это функция называется функцией правдоподобия. Так как выборочные значения определяются в результате измерений, L является функцией только . Удобнее рассматривать 
; вследствие монотонности логарифма максимумы L и достигаются при одном и том же значении . Это значение можно найти из уравнения
Решение этого уравнения 
надувается оценкой максимального правдоподобия вектора b, если действительно зависит от выборочных значений 
. В этом случае необходимо знать, не только ковариационную матрицу помехи, но и вед совместного распределения вероятностей её выборочных значений.
4) Байесовские оценки. В этом случае необходимо еще большая априорная информация. Как показано в [3], должны быть заданы плотности распределения вероятностей x, n, u ,b.
Таким образом, при оценивании методом наименьших квадратов предполагаемся, что динамика объекта может быть аппроксимирована выбранной моделью, при получении Марковских оценок считается также известной ковариационная матрица шума. Для вычисления оценок максимального правдоподобия необходимо знание плотности вероятности измеряемого случайного процесса, и наконец, байесовские оценки требуют знания априорных плотностей вероятности неизвестных параметров и величины штрафа за ошибки. Как следует из этих определений, наиболее простым и эффективным по объему исходной информации об объекте является первый метод-метод наименьших квадратов, следовательно, получение математических моделей процессов первичной обработки хлопка-сырца в виде множественных уравнений (линейных или нелинейных) по методу наименьших квадратов в принципе даёт возможность оценить в первом приближении влияние большого количества факторов на параметр оптимизации процесса. При этом получаемое уравнение гиперплоскости указывает направление и крутизну наклона (градиент) изменения параметра в направлении к экстремуму в некоторой ограниченной области.
При относительно невысокой корреляции входных переменных и наличии некоторой априорной информации о степени и характере связи между переменными процесса одним из эффективных способов построения регрессионных моделей является метод Брандона [2, 4].
Литература:
- Советов Б. Я, Яковлев С. А. Моделирование динамических систем. – М.: Высш. шк., 1998. – 319 с.
- Барский Л. А., Рубинштейн Ю. Б. Кибернетические методы в обогащении полезных ископаемых. – М.: Наука, 1970. – 312 с.
- Корякова О. Г., Маслюк Е. Г. Проблемы построения многоуровневых систем принятия решений // Ж «Исследование операций и АСУ». – 2003. – Вып. 36. – С. 79 – 82.
- Голубев В. О. Литвинова Т. Е. Реализация алгоритма построения статистической модели объекта по методу Брандона/ Math Designer, 2012. – 1-13 с.
